汉诺塔问题

问题描述

汉诺塔问题是由汉多放置在三个塔座上的盘子组成的一个古老的难题，如图1所示。

所有盘子的直径是不同的，并且盘子中央都有一个洞以使它们刚好可以放到塔座上。所有的盘子刚开始都放在塔座A上。这个难题的目标是将所有的盘子都从塔座A移动到塔座C上。每一次只可以移动一个盘子，并且任何一个盘子都不可以放在比自己小的盘子之上。

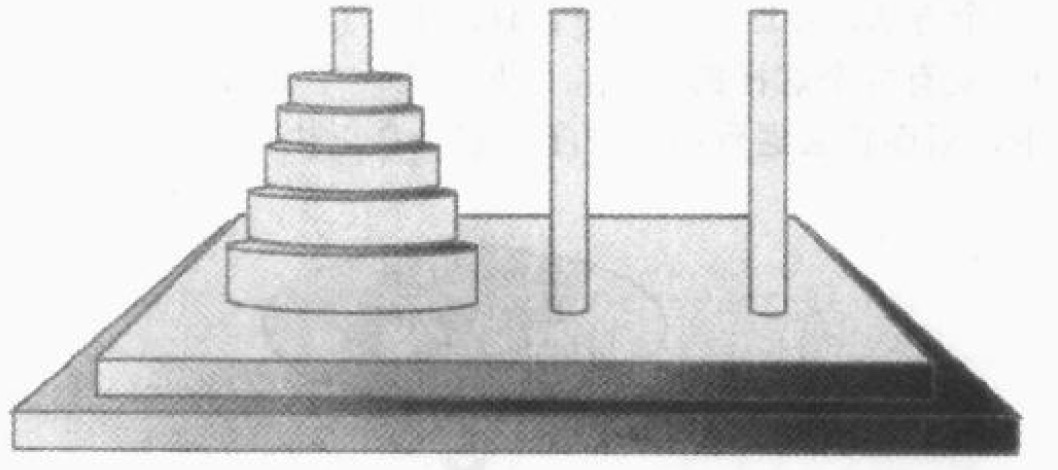
　　　　　　　　　　　　　　图 1   汉多塔

递归算法实现步骤

用子树的概念可以递归地表示出汉诺塔难题的解决办法。假设想要吧所有的盘子从原塔座上（称为S）移动到目标塔座上（称为D）。又一个可以使用的中介塔座（称为I）。假定在塔座S上有n个盘子。算法如下：

1. 从塔座S移动包含上面的n-1个盘子的子树到塔座I上。
2. 从塔座S移动剩余的盘子（最大的盘子）到塔座D上。
3. 从塔座I移动子树到塔座D。

响应代码清单如下

public class TowerApp {

    public static void main(String[] args) {
        int nDisks = 3;
        doTowers(nDisks, 'A', 'B', 'C');
    }

    private static void doTowers(int topN, char from, char inter, char to) {
        if (topN == 1) {
            System.out.println("Disk 1 from " + from + " to " + to);
        } else {
            doTowers(topN - 1, from, to, inter); // from -> inter
            System.out.println("Disk " + topN + " from " + from + " to " + to);
            doTowers(topN - 1, inter, from, to); // inter -> to
        }
    }
}