数组索引的kdtree建立及简明快速的k近邻搜索方法
1. kdtree概念
kd树(k-dimensional树的简称),是一种分割k维数据空间的数据结构,主要应用于多维空间关键数据的搜索,如范围搜索和最近邻搜索。
如下图所示,在既定的分割维度上,每一个根节点的值均大于其左子树,并小于其右子树。这样的二叉树,对于搜索某个点的最临近点或k近邻点,是十分高效快速的。
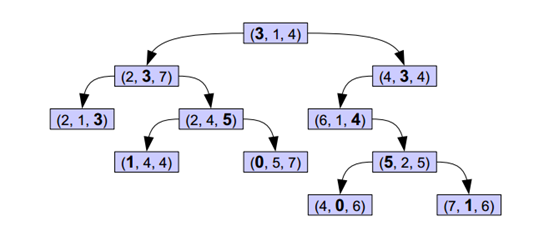
2. 建立kdtree
建立kdtree,主要有两步操作:选择合适的分割维度,选择中值节点作为分割节点。分割维度的选择遵循的原则是,选择范围最大的纬度,也即是方差最大的纬度作为分割维度;分割节点的选择原则是,将这一维度的数据进行排序,选择正中间的节点作为分割节点,确保节点左边的点的维度值小于节点的维度值,节点右边的点的维度值大于节点的维度值。
建立kdtree可遵循以下步骤:
1) 建立一维数组,存储每一个点的索引,并进行随机打乱。
2) 定义合适的kdtree函数定义,方便进行递归建树。
3) 编写分割维度函数
4) 编写选择分割节点函数
5) kdtree函数功能实现:选择分割维度,选择分割节点,将节点左边的数据进行递归建立左子树,将节点右边的数据进行递归建立右子树
下面通过实际代码,讲解kdtree建立的过程:
1)数据及索引的存储定义
无论是数据还是索引均存储在一维数组中,通过二维指针数组来索引,用一个指针数组来存储每一维数据的起始地址,用另一个指针数组来存储每一类索引的起始位置,比如分割维度、父节点、左子树、右子树
/* * dataPtr一维数组表示多维数组 * 数据排布方式:{[x1, x2, x3……], [y1, y2, y3……], [z1, z2, z3……], ……} */ /* * 所有数据存储在一维数组dataPtr里,data分别是x/y/z等数据的起始地址 * 因此,建树及knn只需传递数据的索引编号即可 */ float **data; float *dataPtr; int **tree; // 4 * n :分割维度、父节点、左子树、右子树 int *treePtr; // 使用一维数据表示二维数组,存储建立的kdtree索引
对定义的数组进行初始化操作:
1 int ZtKDTree::setSize(int dimension, unsigned int sz) 2 { 3 nDimension = dimension; // 数据的维度 4 treeSize = sz; // 数据的总数 5 6 if (nDimension > 0 && treeSize > 0) 7 { 8 offset = new double[nDimension]; 9 10 tree = new int *[4]; 11 treePtr = new int[4 * treeSize]; 12 for (int i = 0; i < 4; i++) 13 { 14 tree[i] = treePtr + i * treeSize; 15 } 16 17 data = new float *[nDimension]; 18 dataPtr = new float[nDimension * sz]; 19 for (int i = 0; i < nDimension; i++) 20 { 21 data[i] = dataPtr + i * treeSize; 22 } 23 } 24 25 return 0; 26 }
2) kdtree建立准备,建立一维数组存储数据索引,定义建树函数
使用一维数组存储每一个数据的索引,并进行随机打乱,建树过程中,可以通过索引来访问数据,并且不会打乱原来数据的顺序,快速排序等操作也不必操作数据,只需操作索引即可
1 int buildTree() 2 { 3 std::vector<int> vtr(treeSize); 4 5 for (int i = 0; i < treeSize; i++) 6 { 7 vtr[i] = i; 8 } 9 10 std::random_shuffle(vtr.begin(), vtr.end()); 11 12 treeRoot = buildTree(&vtr[0], treeSize, -1); // 根节点的父节点是-1 13 14 return treeRoot; 15 } 16 17 // 建立kdtree函数 18 int buildTree(int *indices, int count, int parent)
3)分割维度函数编写
分割维度的选择至关重要,选择合适的维度,可提高建树效率及搜索效率。计算当前空间的所有数据每一维度的方差,选择方差最大的维度作为分割维度,并顺便传出维度均值,以用于节点选择函数。

1 int chooseSplitDimension(int *ids, int sz, float &key) 2 { 3 int split = 0; 4 5 float *var = new float[nDimension]; 6 float *mean = new float[nDimension]; 7 8 int cnt = std::min((int)SAMPLE_MEAN, sz);/* cnt = sz;*/ 9 double rt = 1.0 / cnt; 10 11 for (int i = 0; i < nDimension; i++) 12 { 13 double sum1 = 0, sum2 = 0; 14 for (int j = 0; j < cnt; j++) 15 { 16 sum1 += rt * data[i][ids[j]] * data[i][ids[j]]; 17 sum2 += rt * data[i][ids[j]]; 18 } 19 var[i] = sum1 - sum2 * sum2; 20 mean[i] = sum2; 21 } 22 23 double max = 0; 24 25 for (int i = 0; i < nDimension; i++) 26 { 27 if (var[i] > max) 28 { 29 key = mean[i]; 30 max = var[i]; 31 split = i; 32 } 33 } 34 35 delete[] var; 36 delete[] mean; 37 38 return split; 39 }
4)节点选择函数编写
这步操作主要是选择中值节点,但是并不是说要把全部数据进行排序,排序太费时了。使用维度均值进行一趟快速排序,将数据分为两部分,大于均值的数据、小于均值的数据,然后从小于均值的空间中选择最大的节点作为父节点,这样就保证左子树所有节点小于父节点,右子树所有节点大于父节点。

1 int chooseMiddleNode(int *ids, int sz, int dim, float key) 2 { 3 int left = 0; 4 int right = sz - 1; 5 6 while (1) 7 { 8 while (left <= right && data[dim][ids[left]] <= key) //左边找比key大的值 9 ++left; 10 11 while (left <= right && data[dim][ids[right]] >= key) //右边找比key小的值 12 --right; 13 14 if (left > right) 15 break; 16 17 std::swap(ids[left], ids[right]); 18 ++left; 19 --right; 20 } 21 22 23 // 找出左子树的最大值作为根节点 24 float max = -9999999; 25 int maxIndex = 0; 26 for (int i = 0; i < left; i++) 27 { 28 if (data[dim][ids[i]] > max) 29 { 30 max = data[dim][ids[i]]; 31 maxIndex = i; 32 } 33 } 34 35 if (maxIndex != left - 1) 36 { 37 std::swap(ids[maxIndex], ids[left - 1]); 38 } 39 40 return left - 1; 41 }
5)建树
完成以上工作后,建树就很简单了

1 int buildTree(int *indices, int count, int parent) 2 { 3 if (count == 1) 4 { 5 int rd = indices[0]; 6 tree[0][rd] = 0; 7 tree[1][rd] = parent; 8 tree[2][rd] = -1; 9 tree[3][rd] = -1; 10 11 return rd; 12 } 13 else 14 { 15 float key = 0; 16 int split = chooseSplitDimension(indices, count, key); 17 int idx = chooseMiddleNode(indices, count, split, key); 18 19 // rd 是实际点的下标, idx是点的索引数组的下标 20 int rd = indices[idx]; 21 22 tree[0][rd] = split; // 分割维度 23 tree[1][rd] = parent; 24 25 if (idx > 0) 26 { 27 tree[2][rd] = buildTree(indices, idx, rd); 28 } 29 else 30 { 31 tree[2][rd] = -1; 32 } 33 34 if (idx + 1 < count) 35 { 36 tree[3][rd] = buildTree(indices + idx + 1, count - idx - 1, rd); 37 } 38 else 39 { 40 tree[3][rd] = -1; 41 } 42 43 return rd; 44 } 45 }
3. k近邻搜索
最临近搜索即是查找距离查找点最近的k个点。在讲述k临近搜索之前,先讲述下最近邻搜索的概念。
最近邻搜索的基本思路是:从根节点开始,通过二叉树搜索,如果节点的分割维度值小于查找点的维度值表示查找点位于左子树空间中,则进入左子树,如果大于则进入右子树,直到达到叶子节点为止,将搜索路径上的每一个节点都加入到路径中;然后再回溯搜索路径,并判断未加入路径的其他子节点空间中是否可能有距离搜索点更近的节点,如果有可能,则遍历子节点空间,并将遍历到的节点加入到搜索路径中,重复这个过程直到搜索路径为空。
理解了最近邻搜索的思路,就很容易实现k近邻搜索了,k近邻搜索的思路是:同样是先遍历kdtree,将遍历到的节点加入到搜索路径中,然后回溯路径;建立最大堆,在回溯路径中,将小于堆顶最大距离的节点加入堆,直到搜索路径为空。
实际实现过程中,需要注意的是,先出队列的是叶子节点,距离查找点比较近,最先加入最大堆,从而堆顶距离比较小,在最大堆不满时,进行距离判断,可能会将在k近邻范围内的节点排除掉,因此预先加入一个极大距离节点,可避免最大堆不满时,排除掉正确的节点。

1 struct NearestNode 2 { 3 int node; 4 float distance; 5 NearestNode() 6 { 7 node = 0; 8 distance = 0; 9 } 10 NearestNode(int n, float d) 11 { 12 node = n; 13 distance = d; 14 } 15 }; 16 17 struct cmp // 将最大的元素放在队首 18 { 19 bool operator()(NearestNode a, NearestNode b) 20 { 21 return a.distance < b.distance; 22 } 23 }; 24 25 int findKNearests(float *p, int k, int *res) 26 { 27 std::priority_queue<NearestNode, std::vector<NearestNode>, cmp> kNeighbors; 28 std::stack<int> paths; 29 30 // 记录查找路径 31 int node = treeRoot; 32 while (node > -1) 33 { 34 paths.emplace(node); 35 36 node = p[tree[0][node]] <= data[tree[0][node]][node] ? tree[2][node] : tree[3][node]; 37 } 38 39 // 预先加入一个极大节点 40 kNeighbors.emplace(-1, 9999999); 41 42 // 回溯路径 43 float distance = 0; 44 while (!paths.empty()) 45 { 46 node = paths.top(); 47 paths.pop(); 48 49 distance = computeDistance(p, node); 50 if (kNeighbors.size() < k) 51 { 52 kNeighbors.emplace(node, distance); 53 } 54 else 55 { 56 if (distance < kNeighbors.top().distance) 57 { 58 kNeighbors.pop(); 59 kNeighbors.emplace(node, distance); 60 } 61 } 62 63 if (tree[2][node] + tree[3][node] > -2) 64 { 65 int dim = tree[0][node]; 66 if (p[dim] > data[dim][node]) 67 { 68 if (p[dim] - data[dim][node] < kNeighbors.top().distance && tree[2][node] > -1) 69 { 70 int reNode = tree[2][node]; 71 while (reNode > -1) 72 { 73 paths.emplace(reNode); 74 75 reNode = p[tree[0][reNode]] <= data[tree[0][reNode]][reNode] ? tree[2][reNode] : tree[3][reNode]; 76 } 77 } 78 } 79 else 80 { 81 if (data[dim][node] - p[dim] < kNeighbors.top().distance && tree[3][node] > -1) 82 { 83 int reNode = tree[3][node]; 84 while (reNode > -1) 85 { 86 paths.emplace(reNode); 87 88 reNode = p[tree[0][reNode]] <= data[tree[0][reNode]][reNode] ? tree[2][reNode] : tree[3][reNode]; 89 } 90 } 91 } 92 } 93 } 94 95 if (!res) 96 { 97 res = new int[k]; 98 } 99 100 int i = kNeighbors.size(); 101 while (!kNeighbors.empty()) 102 { 103 res[--i] = kNeighbors.top().node; 104 kNeighbors.pop(); 105 } 106 107 return 0; 108 }




