杂题（一）
你会用到的链接：DS 乱做。
CF1097F Alex and a TV Show
niubi bitset 题。
维护 \(n\) 个初始为空的可重集，支持以下操作：
1 x v：令集合 \(x\) 等于 \(\{v\}\)。
2 x y z：令集合 \(x\) 等于集合 \(y\) 与 \(z\) 的并。
3 x y z：令集合 \(x\) 等于集合 \(y\) 与 \(z\) 的积，\(A*B=\{\gcd(a,b)|a\in A,b\in B\}\)
4 x v：询问 \(v\) 在集合 \(x\) 中出现次数模 \(2\) 的结果。\(1\leq n\leq 10^5,1\leq q\leq 10^6,1\leq v \leq 7000\)。
注意到值域很小，又考虑需要维护 \(2\) 和 \(4\) 操作，直接上 bitset，\(2\) 操作就变成了一个异或的过程。
考虑如何维护 \(3\) 操作。直接用目前的 bitset 是不好做的，考虑将 bitset 维护的东西变化一下。因为乘法涉及到一个 \(\gcd\)，首先我们肯定考虑列出暴力的式子考虑能不能用各种反演搞定它。
后面两个东西形式相似，考虑把它们用一个函数代替。设 \(f(S,p)=\sum_{ip\in S}1\)。式子则变成：
显然是不怎么好维护的，但是根据操作 \(4\) 的询问，观察到该式子后半部分是一个乘法，考虑直接用 bitset 维护每个集合的 \(f(S,p)\)。
首先考虑 \(2\) 操作是否一致。\(f(S,p)\) 的实际意义是什么？是 \(S\) 中 \(p\) 的倍数的位出现次数模 \(2\)。这个显然是可以直接异或合并的。
然后考虑 \(3\) 操作。考虑列一个 \(f(S,p)\) 和 \(f(A,p),f(B,p)\) 的关系式，就用刚刚我们推出来 \(S_u\) 与它们的关系式来推即可。
极好！这个乘法在二进制中相当于一个按位与。
剩下一个 \(4\) 操作。不是之前我们才推了一个 \(S_u\) 关于其合并过来的式子吗？我们把其中的 \(f(A,ud)f(B,ud)\) 换成 \(f(S,ud)\)，有：
我们只需要求这个式子模 \(2\) 的值就行了，所以考虑这个乘法我们依然可以直接搞一个 bitset 来乘，最后统计其 count 就行了。具体地，对于每一个 \(u\) 处理出 \(M_u\) bitset，其中对于所有 \(d\)，\(ud\) 位置填 \(\mu(d)\)。注意到是模 \(2\)，所以 \(-1\) 或 \(1\) 都填 \(1\) 就行了。
对于每一个数预处理出当只有一个数 \(v\) 在集合中的 \(f\) 函数 bitset。总时间复杂度 \(O(\frac{qv}{\omega}+v\ln v)\)。
CF1497D Genius
有 \(n\) 个问题，每个问题有附加值 \(c_i=2^i,tag_i,s_i\)。
定义 \(IQ\) 为一个解决问题时的参数，初始为 \(0\)。解决完 \(i\) 问题后，如果你想解决 \(j\) 问题，你需要保证 \(IQ<|c_i-c_j|,tag_i\not= tag_j\)，这样做的权值是 \(|s_i-s_j|\)，解决完后 \(IQ\) 会变为 \(|c_i-c_j|\)。
初始你可以选择一个问题开始解决，任意问题可以被重复解决，问所有解决的过程结束后的权值和最大值。
\(1\leq n\leq 5000\)。
这题我的想法是一次转移一定形如往前搞定一个，然后再往后解决一个，但是有 \(tag\) 的存在，这样做就是错误的，因为需要存每一个数前面被哪个数转移的，原本是可以滚动前缀和优化的，但是 \(tag\) 的存在使得我们不能这样优化。
考虑我们对于所有可能的转移按 \(IQ\) 需求值排序，因为这个题的性质，其实就是 \(i=1\to n,j=i-1\to 1\) 的枚举方式，然后这里直接转移就是正确的，因为每一步转移都满足 \(IQ\) 的限制，而 \(tag\) 的限制判一下就好了。
因为每种转移只可能有一次，且显然无法在一种 \(IQ\) 的转移中成环的转移，所以可以直接互相转移，设 \(f_i\) 为目前解决到 \(i\) 权值最大的值，直接转移即可。时间复杂度 \(O(n^2)\)，空间复杂度 \(O(n)\)。
CF212D Cutting a Fence
给定一个序列 \(a\)，定义一个函数 \(f\) 为：
\[f(k)=\frac{\sum_{x=1}^{n-k+1}\min_{i=x}^{x+k-1}(a_i)}{k} \]给定 \(q\) 次询问，每次询问 \(f(i)\) 的值。
\(1\leq n\leq 10^6\)。
这题有很多做法。我直接暴力分治，用一些双指针获得一个 \(O(n\log n)\) 的复杂度，实际上这个题可以做到 \(O(n)\) 的。
首先我们其实可以预处理出来一个数左边第一个小于它的数，右边第一个小于等于它的数，跨过该点的所有区间答案就是该点的值，同时我们不重不漏地计算到了所有区间。
我们发现如果枚举一边，另外一边的贡献对于 \(f\) 序列是一个区间，这里我们可以差分。根据笛卡尔树启发式合并的结论，我们有：
其中 \(l_i\) 和 \(r_i\) 就是预处理出来左右数的位置。所以我们可以暴力枚举差分。
当然如果再观察仔细一点，不难发现每个区间的贡献是一样有关系的，这里可以二阶差分处理它。时间复杂度线性。
ARC146D >=<
求构造一个长度为 \(n\) 而每个数取 \([1,m]\) 之间的“完美序列”\(A\) ，使得其中所有数之和最小化。如果不存在，输出 \(-1\) 。
完美序列的定义：对于所有 \(K\) 个约束条件，对于第 \(i\) 个约束条件，满足以下三者之一：
- \(A_{p_i}<x_i\) 且 \(A_{q_i}<y_i\) ；
- \(A_{p_i}=x_i\) 且 \(A_{q_i}=y_i\) ；
- \(A_{p_i}>x_i\) 且 \(A_{q_i}>y_i\) 。
\(1\le n,m,k\le 2\times 10^5\) 。数据合法。
这个限制非常不好看，考虑把它们化成一样的形式。不难发现我们可以把它们化成两个 \(A\leq x\Leftrightarrow B\leq y\) 的限制，分别是：
当然你这个时候就可以直接 2-sat 启动，但是需要注意到的是，你需要使得所有数之和最小化，这个放到 2-sat 中是比较难做的。
考虑增量法，即观察到如果只加，一个限制最多被打破一次，考虑我们先将所有值赋为 \(1\)，然后如果有限制被打破，那么就把第二个数放到限制之外。这是一种调整的思想，因为打破之后你只可能把这个数放到比某个值大的地方，而值越大打破的限制越多，就越不优。这样做有点像这些限制不得不被打破的感觉，就是这样才能保证最优。随便维护一下即可，复杂度线性或 1log。
CF1422F Boring Queries
见 DS 乱做。
CF811E Vladik and Entertaining Flags
见 DS 乱做。
CF1603C Extreme Extension
对于一个数列，定义一次操作为选择数列中任何一个元素 \(a_i\) ，将这个位置替换成两个正整数 \(x,y\) 满足 \(x+y=a_i\)。
定义一个数列的极端值为将这个数列变成不降数列的最小操作次数。
给定一个长度为 \(n\) 的数列 \(a\) （ \(1\leq a_i\leq 10^5\) ），让你求它的所有非空子段的极端值之和，对 \(\text{998244353}\) 取模。
一个测试点中有多组数据，保证所有数据 \(n\) 的规模总和不超过 \(10^5\)。
老题重做。这个题当时我直接就是没做出来，现在大概是会了。
考虑所有非空子段这个东西该怎么处理。一种容易的想法是分治或者扫描线。但是这个题显然和分治不沾边，因为右侧的限制数等价于每个位置的限制数，分治一定劣于扫描线。
注意到一个性质，就是一个点如果分成 \(j\) 份，那么分出来的最大值为 \(\lceil\frac{a_i}{j}\rceil\)，最小值为 \(\lfloor\frac{a_i}{j}\rfloor\)。考虑我们对于每个点存一个限制 \(p\)，代表这个点分出来最小值为 \(p\) 的方案数和极端值之和。我们发现根据整除分块的性质，至多有 \(O(\sqrt {a_i})\) 个不同的限制，那么倒序 DP 即可。
最后一个细节就是怎么确定一个限制对应的 \(j\) 最小值。按照定义推式子可以得到，设限制为 \(p\)，\(j=\lceil\frac{n}{p}\rceil\)。使用滚动哈希表维护，比较卡，时间复杂度 \(O(n\sqrt {a_i})\)，当然可以用另外的东西代替哈希表。
CF1603D Artistic Partition
对于给定的正整数 \(l\leq r\)，定义 \(c(l,r)\) 为满足下列条件的正整数对 \((i,j)\) 的数量：
- \(l\leq i\leq j\leq r\)；
- \(\gcd(i,j)\geq l\)。
给定正整数 \(k\leq n\)。对所有满足 \(0=x_1 < x_2 < \cdots < x_k < x_{k+1}=n\) 的整数序列 \((x_1,...,x_{k+1})\)，计算 \(\sum_{i=1}^kc(x_i+1,x_{i+1})\) 的最小值。你需要回答 \(T\) 组询问。
对全部数据，\(1\leq T\leq 3\times 10^5\)，\(1\leq k\leq n\leq 10^5\)。
非常牛逼的一道题。
首先是最关键的一个性质，\(k\geq \log n\) 的时候答案就是 \(n\)，即没有额外贡献。具体就是发现我们可以 \([2^k,2^{k+1}-1]\) 分段，显然区间中没有不同元素使得 \(\gcd\) 在区间中的。
剩下的，考虑不难发现这个显然有四边形不等式（交叉优于包含），因为包含的时候多了一个 \(\gcd(l-1,r+1)\) 的贡献。考虑推式子计算。
推式子后，移动右端点是 \(O(d(i))\) 的，因为每个点会被遍历到 \(O(\log n)\) 次，所以这个东西均摊下来单次分治复杂度是 2log 的。左端点则比较容易，就是一个欧拉函数的前缀和。
那么使用分治就能做到 \(O(n\log^3 n)\) 的复杂度。
CF845F Guards In The Storehouse
给定一个 \(n\times m\) 的网格，有些位置是障碍（
x），有些位置是空地（.）。可以在每一个空地处放一个摄像头，这个摄像头会向右，向下监视第一个障碍前的所有方格。现在你需要在空地上安排摄像头，使得最多 \(1\) 个空地没有被摄像头监视。输出方案数对 \(10^9+7\) 取模。
\(n,m,nm \le 250\)。
注意到 \(nm\leq 250\)，所以边长最小值只有 \(16\)，这里直接轮廓线就行了。
主要就是观察到某一边可状压的一个性质。
CF1137C Museums Tour
一个国家有 \(n\) 个城市，通过 \(m\) 条单向道路相连。有趣的是，在这个国家，每周有 \(d\) 天，并且每个城市恰好有一个博物馆。
已知每个博物馆一周的营业情况（开门或关门）和 \(m\) 条单向道路，由于道路的设计，每条道路都需要恰好一个晚上的时间通过。你需要设计一条旅游路线，使得从首都：\(1\) 号城市开始，并且当天是本周的第一天。每天白天，如果当前城市的博物馆开着门，旅行者可以进入博物馆参观展览，否则什么也做不了，这一天的晚上，旅行者要么结束行程，要么通过一条道路前往下一个城市。当然，旅行者可以多次经过一个城市。
要求让旅行者能够参观的不同博物馆数量尽量多（同一个城市的博物馆参观多次仅算一次），请你求出这个最大值。
\(1\le n\le 100,000\)，\(0\le m\le 100,000\)，\(1\le d\le 50\)。
考虑直接建一个按题意的 \(k\) 层循环分层图。不难发现对于一个点，如果有 \(a\) 时刻可达 \(b\) 时刻，那么 \(b\) 时刻也一定可达 \(a\) 时刻。所以建出分层图之后缩点求出每个连通块的答案，这个时候做一下去重，然后发现答案就是点权最长路了。
为什么？因为这个结构满足如果某个点 \(a\) 时刻不可达 \(b\) 时刻，那么 \(b\) 时刻就不可达 \(a\) 时刻，所以 \(a\) 时刻和 \(b\) 时刻的连通块根本互不连通，最长路中也一定只会连接其中一个联通块。
直接缩点拓扑排序即可。注意这题卡巨大空间，需要链式前向星。还卡巨大栈空间，需要 inline。
时间复杂度 \(O((n+m)d)\)。
CF884E Binary Matrix
给定一个 01 矩阵，求 1 的四连通块个数。
\(1\leq n\leq 2^{12},1\leq m\leq 2^{14}\)。空间限制 16MB。
这个空间限制使得不能直接 DFS。
考虑沿用之前维护区间连通块的那个题的线段树思路，将并查集的过程滚动掉，同时将每个点的 \(fa\) 尽量往目前的那一行靠，这样容易实现。时间复杂度为 \(O(nm\alpha(m))\)。
CF1946F Nobody is needed
见 DS 乱做。
CF1500C Matrix Sorting
给你两个 \(n\times m\) 的矩阵 \(A,B\)（\(1\le n,m\le 1500\)），矩阵的元素均为 \([1,n]\) 内的整数。
每一次操作你可以选定一列作为每一行的关键字，按照关键字从小到大的顺序把所有行排序得到一个新矩阵。这里使用的排序是稳定的，即如果有两行的关键字相同，则按照在原矩阵的先后顺序排序。
你可以进行不超过 \(5000\) 次操作，问你能否将 \(A\) 变成 \(B\)。不能变成输出 \(-1\)，否则输出一种可行的操作序列。
很巧妙的一个构造题。
首先不难发现目标矩阵如果和原矩阵不一样的话，至少会有一列满足是按升序排序的。
首先用哈希和这个升序的列得到目标矩阵的行在原矩阵的编号。如果用相同的行可以直接不管。
我们定义解决两个数的顺序为经过一次排序之后后面都不会改变这两个数的顺序，并且在最终的排序中这两个数的顺序正确。显然只需要在已排序列讨论相邻的两个数的顺序就行。
倒序考虑所有排序操作。显然一次排序是可以解决一些数对的。我们把需要解决的数对（因为只需要相邻的，所以是 \(O(n)\) 个）单独拎出来建点。然后对于每一列讨论这些所有的数对，如果满足排序之后能解决这两个点的顺序，那么这个列的点连向对应数对的点。如果反而会倒置顺序，那么就对应数对连向这个列的点，表示我们需要后面先解决完这些点对才能考虑对这一行排序。我们在原矩阵最后加一列 \(1\sim n\)，对我们建出来的图拓扑排序，如果能排到最后这一列的，那么直接将拓扑序倒着输出即可。
需要注意的是，这里的拓扑排序和传统意义上的拓扑排序不同。因为解决一个点对的过程只需要一次，所以只需要一个入度被选就能选到解决点对的点。
CF1713F Lost Array
抽象高级题。
给出一个从 \(1\) 到 \(n\) 的数组 \(a\)。有一个从 \(0\) 开始标号的大小为 \((n+1)\times (n+1)\) 的矩阵 \(b\)，通过以下方式生成：
- 对于 $0 \leq i \leq n , b_{i,0} = 0 $。
- 对于 $1 \leq i \leq n , b_{0,i} = a_{i} $。
- 对于 \(1 \leq i, j \leq n , b_{i,j} = b_{i,j-1} \oplus b_{i-1,j}\)。
现在，给出 $ b_{1,n}, b_{2,n}, \ldots, b_{n,n} $，试还原出一个满足条件的 \(a\) 数组，或者报告无解。
\(1\leq n\leq 5\times 10^5\)。
真的很抽象啊。
首先尝试直接描述题意，首先把矩阵的右上角当做原点，也就是说把 \(a\) 倒序看。发现一个位置 \(a_i\) 贡献到目标 \(b_j\)，需要走 \(i+j\) 步，一共有 \(\binom {i+j}{i}\) 种贡献方式。这里显然只有奇数次贡献才真正贡献到了，所以这里我们需要让这个组合数为奇数。
根据库默尔定理（或者手玩），发现当且仅当 \(i\operatorname{and}j=0\) 时才能满足奇数的限制，这也就是说 \(i\) 是 \(j\) 补集的子集。因为是异或，所以直接往回做一遍子集异或就行了。根本不是！你这里的补集出了问题，因为是补集，所以无论是你得到的补集信息还是你推到的补集信息，都是需要整个 \(2\) 的正整数次幂的信息才能得到。而你只有前 \(n+1\) 项，显然不够。
然后就是神奇 Ad-hoc 部分了。注意到什么是可以直接做逆回去的，显然是只涉及到 \(0\sim n\) 的信息的变换，即没有什么补集之类的神奇变换。拆开 \(\binom {i+j}{i}\)。几何意义上，我们先贡献到该矩阵变换原点之后的主对角线（即原来的副对角线）上，然后再贡献到 \(b\)。惊喜的发现，这里我们的贡献就变成了 \(x\) 是 \(y\) 的子集的形式，这样我们只涉及到 \(0\sim n\) 的超集异或或者子集异或，所以没有什么煞笔的补集问题，直接做回去即可。复杂度 1log。
P7916 [CSP-S 2021] 交通规划
依托臭大粪啊！
给定一个平面上 \(n\) 条水平直线和 \(m\) 条垂直直线，它们相交形成 \(n\) 行 \(m\) 列的网格，从上到下第 \(r\) 条水平直线和从左到右第 \(c\) 条垂直直线之间的交点称为格点 \((r, c)\)。网格中任意两个水平或垂直相邻的格点之间的线段称为一条边，每条边有一个非负整数边权。
进行 \(T\) 次询问，每次询问形式如下：
给出 \(k\)（\(T\) 次询问的 \(k\) 可能不同）个附加点，每个附加点位于一条从网格边缘向外出发的射线上。所有从网格边缘向外出发的射线按左上-右上-右下-左下-左上的顺序依次编号为 \(1\) 到 \(2 n + 2 m\)，如下图：
对于每次询问，不同附加点所在的射线互不相同。每个附加点和最近的格点之间的线段也称为一条边，也有非负整数边权（注意，在角上的格点有可能和两个附加点同时相连）。
给定每个附加点的颜色（黑色或者白色），请你将网格内每个格点的颜色染成黑白二者之一，并使得所有两端颜色不同的边的边权和最小。请输出这个最小的边权和。
显然问题等价于一个所有黑点连向白点的最小割。
对于每次询问，建出其对偶图，注意附加点是在射线上，所以附加点之间是一个面。
要分割所有的黑白点，所以关键的面是旁边两个关键点不同颜色的面，跑一遍所有关键面开始的最短路。剩下就是我们需要连接所有关键面，显然最优分割下一定是所有关键面连接的路径不交，可以括号序列描述匹配情况。所以这里有一个容易的区间 DP。
然后就做完了。
CF992E Nastya and King-Shamans
见 DS 乱做。
CF185D Visit of the Great
推一堆式子题。煞笔出题人很会出样例，然后一堆 corner。
\(T(T\leq 10^5)\) 组询问，每组询问给出四个数 \(k,l,r,p\)，其中 \(p\) 为质数。
求 \(\operatorname{lcm}(k^{2^{l}}+1,k^{2^{l+1}}+1,k^{2^{l+2}}+1,\dots,k^{2^{r}}+1)\bmod p\) 的值。
\(k\leq 10^6,l,r\leq 10^{18},p\leq 10^9\)。
直接求所有项的 \(\operatorname{lcm}\) 一定不行，考虑首先求邻项的 \(\gcd\)。设小的一项为 \(p+1\)。
根据辗转相除法，我们可以知道当且仅当 \(2\nmid k\) 时，邻项 \(\gcd\) 为 \(2\)，否则为 \(1\)。所以我们只需要求出所有的乘积之后判断是否需要除以 \(2^{r-l}\) 即可。当然可以容易验证，就算不是相邻两项，\(\gcd\) 也只可能是 \(1\) 或 \(2\)。
当然你需要特判 \(k=1\)。这个时候答案直接就是 \(2\)。
当然你需要特判 \(2|p\)。这个时候 \(2\nmid k\) 答案就是 \(0\)。
反正还有很多特判，这里不一一列举。
理想情况下，我们就只需要求出上面 \(r-l+1\) 个值的乘积就行了。考虑答案等于两个前缀积相除。每个前缀积相当于是对于 \(k^0\sim k^{2^{r+1}-1}\) 求和。等比数列求和即可。
可以容易做到 \(O(T\log r)\)。
CF1325E Ehab's REAL Number Theory Problem
多少道题了啊。唉，
给一些数，每个的因数个数不超过 \(7\)，求最少选出多少个，使得乘积为完全平方。无解输出 \(-1\)。
\(1\leq n\leq 10^5,1\leq a_i\leq 10^6\)。
首先需要一点观察。
然后可以尝试连出一个图，我们只把出现了奇数次的质数拎出来。如果有 \(1\) 个，那么就 \(S\) 和 \(p\) 连边（\(p\) 是那个质数），否则 \(p_1\) 和 \(p_2\) 相连，显然问的就是最小环。
直接做复杂度爆炸。但是排除二元环之后，最优环上显然至少包含一个 \(\leq\sqrt {a_{i}}\) 的数，所以我们只需要对于 \(\leq 10^3\) 的点和 \(S\) 点 BFS 建出以其为根的最短路树更新最小环即可。时间复杂度 \(O(n{\sqrt{a_i}})\)。
P5540 [BalkanOI2011] timeismoney | 最小乘积生成树
给出一个 \(n\) 个点 \(m\) 条边的无向图，第 \(i\) 条边有两个权值 \(a_i\) 和 \(b_i\) 。
求该图的一棵生成树 \(T\) ，使得
\[\left(\sum_{e\in T}a_e\right)\times\left(\sum_{e\in T}b_e\right) \]最小。
\(1\leq n\leq 200,1\leq m\leq 10000,0\leq a_i,b_i\leq 255\) 。
算是典题了吧。这是一类最小乘积问题。
把生成树的 \(\sum a\) 和 \(\sum b\) 这两个属性描述成一个二维上的点 \((\sum a,\sum b)\)。显然最优点一定落于所有点的凸包上，画出最优解所在的反比例函数上即可得出。
然后问题变为如果快速构造出凸包。使用 quick-convex 算法，其主要思想在于在两点间尝试找到更优的一个点。考虑我们首先计算出凸包的最左边点和最下边点，具体可以分别按 \(a,b\) 为第一关键字做一遍最小生成树。
然后考虑对于两点之间的线段（向量）尝试算出在该线段之下的新点。
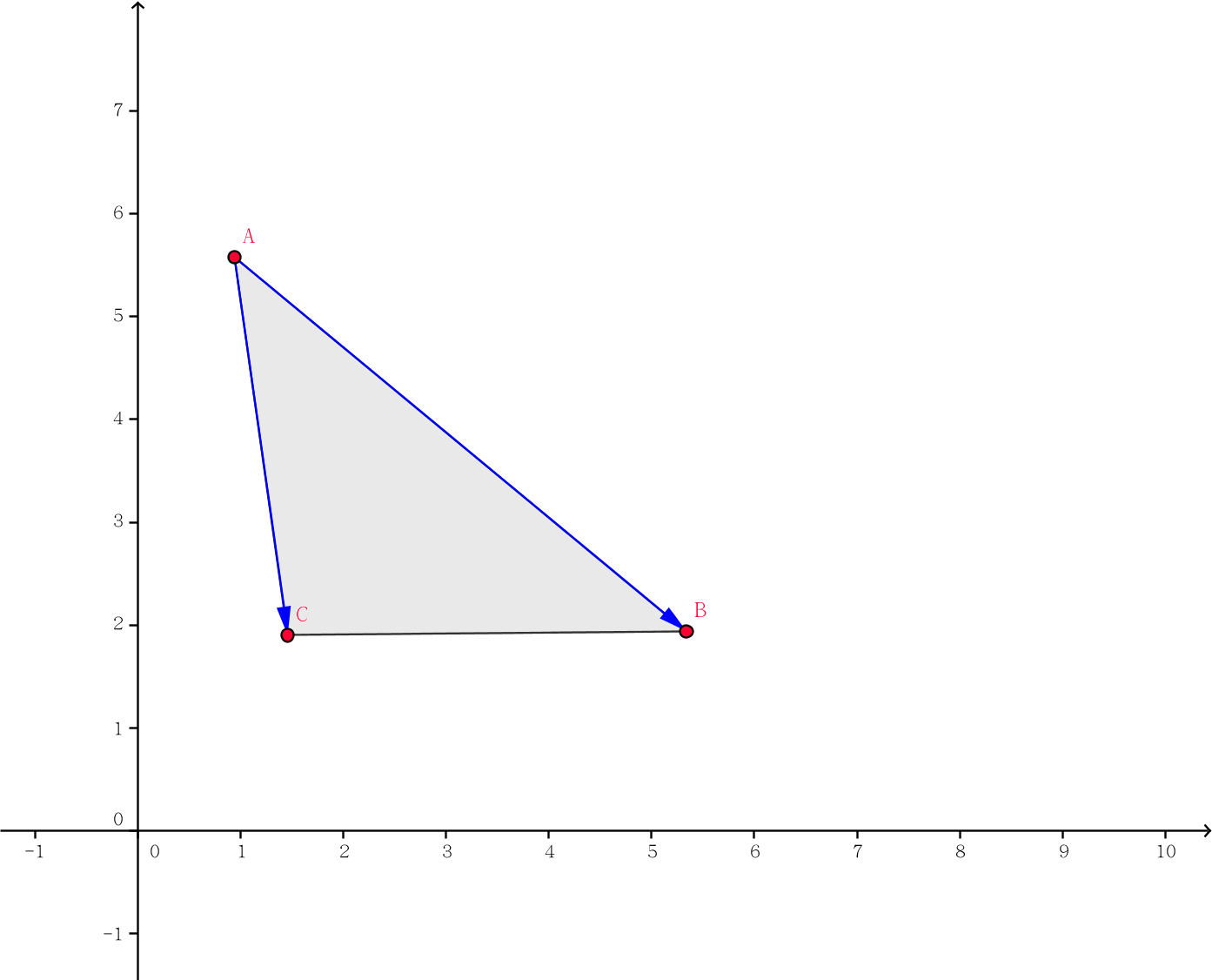
问题变为找到 \(C\) 点，我们可以用向量 \(AB\) 叉上向量 \(AC\) 的最值判断是否存在 \(C\) 点，因为是顺时针叉，所以我们求最小值即可。计算出 \(AB\) 叉 \(AC\) 的表达式，可得其等于 \((x_B-x_A)\times y_C+(y_A-y_B)\times x_C\)。
因为 \(x_C\) 和 \(y_C\) 的意义是 \(C\) 所处的生成树的 \(\sum a\) 和 \(\sum b\)，所以我们可以直接把边权设成 \((x_B-x_A)\times b_i+(y_A-y_B)\times a_i\) 求最小生成树就能得到 \(C\) 点坐标。如果发现叉积为零则 \(C\) 不存在。然后递归 \(AC\) 和 \(CB\) 处理即可。
复杂度钦定能过就行了。
P4180 [BJWC2010] 严格次小生成树
结论！钦定！
小 C 最近学了很多最小生成树的算法，Prim 算法、Kruskal 算法、消圈算法等等。正当小 C 洋洋得意之时，小 P 又来泼小 C 冷水了。小 P 说，让小 C 求出一个无向图的次小生成树，而且这个次小生成树还得是严格次小的，也就是说：如果最小生成树选择的边集是 \(E_M\)，严格次小生成树选择的边集是 \(E_S\)，那么需要满足：(\(value(e)\) 表示边 \(e\) 的权值) \(\sum_{e \in E_M}value(e)<\sum_{e \in E_S}value(e)\)。
这下小 C 蒙了，他找到了你，希望你帮他解决这个问题。
\(N\le 10^5\)，\(M\le 3\times10^5\)，边权 \(\in [0,10^9]\)，数据保证必定存在严格次小生成树。
首先我们知道次小生成树和最小生成树之间差一条边。那严格次小呢？显然也是一条，因为无论选的是哪个最小生成树，最后交换的边的边权对不会改变。
那么这个和直接倍增或者重构树求次小生成树有什么区别吗？我们这次不能直接选用路径上的最大边，因为如果最大边等于目前枚举的非树边就不是严格次小了。所以要倍增维护次大边，简直像史一样。
CF1986G2 Permutation Problem (Hard Version)
给定一个 \(1\sim n\) 的排列 \(p\)，求整数对 \((i,j)\) 的数量，满足 \(1\le i<j\le n\) 且 \(p_i\cdot p_j\) 能被 \(i\cdot j\) 整除。每个测试点 \(t\) 组测试用例。
\(1\le n\le 5\cdot 10^5\)；
\(\sum n\le 5\cdot 10^5\)。
看来难点还是在于第一步和证明复杂度上啊。
首先乘法整除乘法是一个很复杂的模型，肯定先要简化模型。
考虑对于每个 \(i\)，设 \(d=\gcd(i,p_i),a_i=\frac{i}{d},b_i=\frac{p_i}{d}\)。这下上面的问题变成了 \(a_i\times a_j\) 是否整除 \(b_i\times b_j\)。然后因为 \(\gcd(a_i,b_i)=1\)，所以 \(a_i\) 的所有因子只能包含在 \(b_j\)，我们可以转化限制为 \(a_i|b_j\) 且 \(a_j|b_i\)。同时我们需要注意现在 \(a,b\) 都不是排列了。
预处理因数，考虑按值域考虑，枚举 \(a_j\)，枚举其倍数的 \(b_i\) 所有对应的 \(a_i\)，然后再枚举 \(a_j\) 对应的所有 \(b_j\) 枚举因数统计贡献。注意去除算到的 \((i,i)\) 类型的贡献。
乍一看复杂度飞天，其实不然。
首先后半部分其实等于 \(\sum d(b_i)\)，因为 \(b_i\) 是有排列中的某些元素除以某些值得到，所以一定 \(\leq O(n\ln n)\)。
前半部分枚举倍数部分是 \(O(n\ln n)\) 的，但是还要同时枚举对应的 \(a_i\)，这不飞？？？当时看题解的时候我就一直卡在这里。注意到其实 \(b_i\) 一定来源于其倍数，所以 \(b_i\) 总枚举个数是固定 \(O(n\ln n)\) 的，其中总个数指的是每次枚举 \(b_i\) 的时候最多会枚举到的 \((a_i,b_i)\) 对。而在原序列中 \(a_i\) 和 \(b_i\) 一一匹配，所以 \(a_i\) 每次的枚举个数和 \(b_i\) 每次的总枚举个数是一样的，所以复杂度正确。
P11262 [COTS 2018] 题日 Zapatak
先把这个题记录下来。
定义长度均为 \(k\) 的数列 \([a_1,a_2,\ldots,a_k]\) 和 \([b_1,b_2,\ldots,b_k]\) 几乎相等，当且仅当存在恰好一个 \(1\le p\le k\)，使得 \(a_p\neq b_p\)。
定义长度均为 \(k\) 的数列 \([a_1,a_2,\ldots,a_k]\) 和 \([b_1,b_2,\ldots,b_k]\) 相似，当且仅当可以通过重排使得 \(a,b\) 几乎相等。
给定长度为 \(n\) 的数列 \([a_1,a_2,\ldots,a_n]\)。\(m\) 次询问，每次询问给定 \(l_1,r_1,l_2,r_2\)，问 \([a_{l_1},a_{{l_1}+1},\ldots,a_{r_1}]\) 与 \([a_{l_2},a_{{l_2}+1},\ldots,a_{r_2}]\) 是否相似。
\(1\le n,m\le 10^5,0\le a_i\le 10^9,1\le l_1\le r_1\le n,1\le l_2\le r_2\le n,r_1-l_1=r_2-l_2\)。
我的做法是维护和，用 \(g^v\) 作为哈希函数。这个函数在这个题有很好的性质，可以通过差来导出到底差哪些数，然后通过加减哈希值就能判断结果。但是实际上正确率并不是很优秀。
实际上，我们不止可以维护和以得到两数之差，我们还可以维护平方和以得到两数平方差。这样我们就能得到两数分别是什么，然后随便做就行了。
CF1270G Subset with Zero Sum
高明题目，很难想到正解。
给你 \(n\) 个整数 \(a_1 ,a_2 \cdots a_n\)，第 \(i\) 个整数 \(a_i\) 满足 \(i-n\le a_i \le i-1\).
找到一个这些整数的一个非空子集，使得它们的和为 0。可以证明在给出的条件下一定存在这样的子集。如果有多个子集满足条件，输出其中一个。
$ 1\le n \le 10^6 $。
这个限制很奇怪对吧？稍微改写一下，变成了 \(1\leq i-a_i\leq n\)。我们的目标则是 \(\sum_i i-a_i=\sum_i i\)。
我们有 \(n\) 个 \(i-a_i\) 的值，如果直接 \(i\to i-a_i\) 连边，我们会连出若干基环树，不难发现一个环就是答案。拉出一个环即可。
CF1366F Jog Around The Graph
无向图哦。好做一点。
给定一个 \(N\) 个点，\(M\) 条边的无向图，边有长度。 对于每一个 \(k \in [1, T]\)，求出从 \(1\) 号点开始经过 \(k\) 条边的路径的最大长度，输出它们的和。\(N,M\leq 2000, T\leq 10^9\)。答案对 \(10^9+7\) 取模。
考虑最后是无向图，所以我们最后一定是在一个边反复横跳，因为一个环一定不优。这就是和有向图的区别。
我们可以一次 DP 算出 \(k\leq n\) 每个点的答案，然后最后我们会得到 \(O(m)\) 个形如一次函数的答案式子。我们对这些式子求一个凸包即可。可以排序单调栈解决。时间复杂度 \(O(nm)\)。
CF986E Prince's Problem
见 DS 乱做。
CF217E Alien DNA
见 DS 乱做。
P1248 加工生产调度
推式子，还有奇怪的知识...
某工厂收到了 \(n\) 个产品的订单，这 \(n\) 个产品分别在 A、B 两个车间加工，并且必须先在 A 车间加工后才可以到 B 车间加工。
某个产品 \(i\) 在 A、B 两车间加工的时间分别为 \(A_i,B_i\)。怎样安排这 \(n\) 个产品的加工顺序，才能使总的加工时间最短。
这里所说的加工时间是指：从开始加工第一个产品到最后所有的产品都已在 A、B 两车间加工完毕的时间。
\(1\leq n\leq 1000\)。
首先不难发现这个题是确定顺序，根本是不能 DP 的（除非你状压/qd）。
所以直接考虑 exchange arguments。
这里需要钦定一个参数 \(c\) 表示目前还有 \(c\) 分钟 \(B\) 机器才空闲。
钦定 \(s\) 在最优顺序中在 \(t\) 的前面，推一下式子，然后中途把 \(c\) 的限制弱化掉，最后得到 \(\min(a_s,b_t)\leq \min(a_t,b_s)\)。
这个式子具有传递性，但是并不满足严格弱序，具体而言就是没有连等传递性。需要再加一维限制来满足。如果两者相等，我们一定选 \(a_i\) 小的来保证 \(b\) 的连续。
P3400 仓鼠窝
接下来是三个有关于平面上的矩形或正方形的问题。
萌萌哒的 Created equal 是一只小仓鼠，小仓鼠自然有仓鼠窝啦。
仓鼠窝是一个由 \(n\times m\) 个格子组成的行数为 \(n\)、列数为 \(m\) 的矩阵。小仓鼠现在想要知道，这个矩阵中有多少个子矩阵。
比如说有一个 \(2\times 3\) 的矩阵，那么 \(1\times 1\) 的子矩阵有 \(6\) 个，\(1\times 2\) 的子矩阵有 \(4\) 个，\(1\times 3\) 的子矩阵有 \(2\) 个，\(2\times 1\) 的子矩阵有 \(3\) 个，\(2\times 2\) 的子矩阵有 \(2\) 个，\(2\times 3\) 的子矩阵有 \(1\) 个，所以子矩阵共有 \(6+4+2+3+2+1=18\) 个。
可是仓鼠窝中有的格子被破坏了。现在小仓鼠想要知道，有多少个内部不含被破坏的格子的子矩阵。
\(1\leq n,m\leq 3000\)。
每一行维护单调栈，维护类似于前缀和的东西进行累加就行了。时间复杂度 \(O(nm)\)。
CF480E Parking Lot
\(n\times m\) 的矩阵，有一些点不能选。\(k\) 次操作，每次都让一个点变成不可选，每次都问当前可选的最大正方形。\(n,m,k\leq 2000\)。
考虑倒序操作，首先 \(O(nm)\) DP 出答案。具体就是 \(f_{i,j}=\min(f_{i,j-1},f_{i-1,j},f_{i-1,j-1})+1\)。
显然如果答案要变大，那么新的答案一定包含解封的点。所以我们在解封点的行上枚举答案，滑动窗口得到上下最长能拓宽多少格子，来更新答案。
因为答案最大是 \(\min(n,m)\)，所以复杂度正确，为 \(O(nm+nk+mk)\)。
P8922 [MdOI R5] Squares
见 DS 乱做。
CF690A3 Collective Mindsets (hard)
后面还有恶魔 F3。
一共有 \(n\) 个僵尸，每个僵尸头上有一个 \(1 \sim n\) 之间的数字（可重复！），每个僵尸只能看到其他 \(n - 1\) 个僵尸头顶的数字，当然，他们也知道自己的编号。 要求提供一种策略，使所有僵尸只利用自己知道的信息同时猜自己头顶的数字，保证至少有一个僵尸猜对。
\(1 \le T \le 50000 ,2 \le n \le 6 ,1 \le r \le n\)。
高明的题目。首先你把编号去掉，你发现你 \(n=2\) 怎么做都是错的。说明编号还真有用。
考虑有一个很高明的想法，假设我们已经知道和 \(\bmod n\) 的值，那么我们一定能猜对自己头上的数字。而我们有 \(n\) 个人。那么就完了，每个人按照自己的编号猜和。这样至少会有一个人猜中。
P10875 [COTS 2022] 游戏 M
圆和焰在玩游戏。
有一张 \(N\) 个节点的无向图，焰会依次向图中添加 \(M\) 条边。
焰有 \(Q\) 个询问，每次询问给定 \(u,v\)，问：至少添加前多少条边，才能使得 \(u,v\) 间没有割边（换言之，割去任意一条边，都不影响 \(u,v\) 的连通性）。特别地，如果 \(u,v\) 始终不连通或者始终有割边，则输出 \(-1\)。
圆准备要去军训了，所以找来了你解决这个问题。
\(2\le N \le 3\times 10^5\)，\(0\le M\le 3\times 10^5\)，\(1\le Q\le 3\times 10^5\)，\(s_i\neq t_i\)，\(u\neq v\)，\(1\le u,v,s_i,t_i\le N\)。
这个题有很多做法，其中不乏很有启发性的做法。
首先抛开问题本身，如何动态维护边双？入股只考虑加边的话，我们可以缩点，每次把路径上的点全部缩到 LCA 处。这样就能维护了。
接下来有很多处理方式。最无脑的一种是整体二分，这里的整体二分可以通过预处理做到 1log。
考虑不要离线。我们每次缩点的时候将缩的所有点连向 LCA，边权为目前加了多少条边。最后问题变成一颗新树上的边权 \(\max\)，可以重构树，也可以倍增。
题解区还有人启发式合并边双中的标号，顺便处理询问，非常高明。
CF1672H Zigu Zagu
个人差大啊。
你有一个长度为 \(n\) 的二进制串 \(a\)，现在给出 \(q\) 次询问，每次询问给出两个数 \(l,r\)，保证 \(1 \leq l \leq r \leq n\)。
令 \(s=a[l,r]\)，你可以对 \(s\) 做如下操作：
1.选择两个数 \(x,y\)，满足 \(1 \leq x \leq y \leq |s|\)。令子串 \(t=s[x,y]\)，对于所有的 \(1 \leq i \leq |t|-1\)，需要满足 \(t_i \neq t_{i+1}\)，操作才是合法的，否则是不合法的。注意 \(x=y\) 时永远是合法的。
2.从 \(s\) 中删除 \(s[x,y]\)。
对于每一个询问，请求出最少需要多少个操作才能把 \(s\) 变成一个空串。
标记提示：\(s[l,r]\) 表示从 \(l\) 开始,到 \(r\) 结束的子串。
\(\leq n,q \leq 2\times 10^5\)。
你以为是高明 *2700 贪心，但是实际上是一个相对容易的 Ad-hoc 找性质题。
每次删除的字符串形如 010101010。考虑删除 0101010 这种两端相等的字符串，我们减少了序列中一个 00 对。如果删除两端不等的 010101 这种串，减少了 11 和 00 各一个。
所以我们先一直做后面的操作，显然如果一个序列中 00，11 均存在，那么一定存在后面这种子串。然后只剩 00 或 11 时做前面的操作。设 00 数量为 \(x\)，11 为 \(y\)，答案就是 \(\max(x,y)\)，前缀和即可。
CF1580B Mathematics Curriculum
把剩下的五个题扔给下周吧。
求满足以下条件的排列个数：
- 长度为 \(n\)。
- 恰有 \(k\) 个数满足：所有包含这个数的区间中，不同的最大值的个数恰有 \(m\) 个。
答案对 \(p\) 取模。
\(1\leq n\leq 100\)。
五方过 100。这个题正好提醒了我笛卡尔树不是很会，整完所有题解之后我就会去专攻 Hall 定理和笛卡尔树了。
考虑这是一个排列，我们 DP 相对顺序。然后我们发现每次跨过最大值，那么剩下两段原来相对顺序下得到的答案都只需要加一。所以我们设长度为 \(i\) 的排列有 \(j\) 个数最大值个数为 \(k\) 的方案数为 \(f_{i,j,k}\)。
转移则枚举最大值出现在哪里，然后对 \(j\) 做一个卷积即可。需要卡常。当然还要注意合并两个相对顺序排列的那个经典组合数 \(\binom {a+b}a\)。
CF1699E Three Days Grace
确实是一个比较牛逼的题。
给定一个初始有 \(n\) 个元素的可重复集合 \(A\)，其中每个元素都在 \(1\) 到 \(m\) 之间。
每次操作可以将 \(A\) 中的一个元素（称之为 \(x\)）从 \(A\) 中删除，然后在 \(A\) 中加入两个元素 \(p,q\)，满足 \(p\cdot q=x\) 且 \(p,q>1\)。
显然每次操作后 \(A\) 的大小会增加 \(1\)。
定义 \(A\) 的平衡值为 \(A\) 中的最大值减去最小值，求任意次操作（可以是 \(0\) 次）后最小可能的平衡值。
\(1\leq \sum n\leq 10^6,1\leq\sum m\leq 5\times 10^6\)。
一种容易的想法是钦定目标集合的最小值，然后分解 \(A\) 中原来的每个数。这里因为最小值减少的时候，\(A\) 中的每个数会分解的更彻底。所以我们可以降序枚举最小值，每次会更新到的数都一定是新最小值的倍数。这一部分做法就是 \(O(m\ln m)\) 的。
现在我们需要求所有 DP 值的最大值。注意到最大值也是降序，所以我们可以更新所有最大值放进的桶，每次往下枚举最大值，时间复杂度显然是 \(O(m)\)。
然后这个题就做完了。
P11261 [COTS 2018] 直方图 Histogram
线性跑不过 1log/qd。
给定笛卡尔坐标系中的直方图，宽度为 \(n\)，第 \(i\) 格的高度为 \(h_i\)。也就是说，对于 \(\forall 1\le i\le n\)，第 \(i\) 格所占矩形的顶点坐标分别为 \((i-1,0),(i,0),(i-1,h_i),(i,h_i)\)。
给定正整数 \(p\)，求出满足以下条件的矩形的数量：
- 矩形的四个顶点的坐标均为整数；
- 矩形有一条边在 \(x\) 轴上；
- 矩形完全位于直方图内部（可以与边界相切）；
- 矩形的面积至少为 \(p\)。
\(1\le n\le 10^5,1\le p\le 10^{14},1\le h_i\le 10^{9}\)。
根据经典结论，我们把这个直方图类似笛卡尔树分成一些有效矩形，具体就是，每次顶着最小值划分出一个矩形，然后以最小值分割剩下的区间递归处理。
现在我们这里就需要对于每一个边长处理其贡献。如果把底边搞成枚举的边长，不难发现因为 \(h_i\) 太大，不好预处理，考虑我们把竖着的边当成边长。现在贡献有两段，第一段是有关 \(p\) 除以目前枚举的变成，第二段就是所有矩形。注意到，第一段长度最多是 \(n\)，所以我们可以直接预处理第一段。
需要推式子，有一定细节。最后其实有可以规避 int128 的方法，就是答案不会爆 long long，只是那个前缀和会爆。所以我们可以使用 unsigned long long 自然溢出来处理贡献。这样常数就小了。不过还是跑不过 1log。
CF690F3 Tree of Life (hard)
HC2 出大狗屎。
假设有一棵 \(n\) 个点，\(n-1\) 条边的树 \(T\)。
现给定 \(k=2\) 张 \(n-1\) 个节点的无向图 \(G_1,G_2\)，满足 \(G_1,G_2\) 分别由 \(T\) 删去节点 \(a_1,a_2\) 及其连边后打乱标号（用 \(1-n\) 中的所有数字给剩余 \(n-1\) 个节点两两不同地标号）得到，求 \(T\)。
注意 \(a_1\not=a_2\)。\(Z\) 组数据。
\(1\le n\le1000,1\leq Z\leq 20\)。
现在知道了，以后遇到这种题，我们只需要一直无脑往里面加条件直到对为止。
首先，树哈希使用 xor-shift 子树哈希值，然后相加，最后加一个常数的方法。算是经典了。然后用换根判整树同构，当然用重心也行。
然后就是往里填条件的时候了。枚举 T-u 中的 v 和 T-v 中的 u，然后预处理之后可以直接判断森林同构。这一部分是容易的。
然后你发现这个条件根本不够。具体就是你发现一个 \(u,v\) 相邻且其连接子树同构的情况，你任意匹配两点都是对的，但是不一定有解。所以你考虑去枚举 \(u,v\) 重合的子树，将其哈希值算上，然后去算 T-v 中 \(u\) 的子树哈希值之和，去尝试组成 T-u。同理，用一样的方法组成 T-v。这里需要推一推式子。不过这就够了。
如果你还想更牛逼一点，你可以去枚举 deg 之类的，但是没有什么用。时间复杂度 \(O(Zn^2)\)，但是因为预处理信息需要存储，空间较大，所以常数比较大。
CF1320D Reachable Strings
见 DS 乱做。
P8820 [CSP-S 2022] 数据传输
使用 UT 的简单科技。link。
这里就贴一个封装好的板子了。
思想就是使用 lowbit 个数和 lowbit 和都是 1log 来做。当然需要 \(O(n\log n)-O(1)\) LCA，不过懒了就树剖了。
代码
template<class Unit,class T>
struct Tree{
Unit S[M],I;
Tree(const Unit x):I(x){}
T merge=T();
#define pUnit pair<Unit,Unit>
inline pUnit mer(pUnit x,const Unit &y){
x.first=merge(x.first,y);
x.second=merge(y,x.second);
return x;
}
inline pUnit mer(pUnit x,const pUnit &y){
x.first=merge(x.first,y.first);
x.second=merge(y.second,x.second);
return x;
}
int fa[M],dep[M],siz[M],hson[M],dfn[M],rk[M],dfncnt;
vector<int> E[M];
inline void addE(int u,int v){
E[u].push_back(v),E[v].push_back(u);
return;
}
void dfs1(int now,int f){
fa[now]=f;
siz[now]=1;
for(auto p:E[now])if(p^f){
dep[p]=dep[now]+1;
dfs1(p,now);
siz[now]+=siz[p];
if(siz[p]>siz[hson[now]])hson[now]=p;
}
return;
}
int ltop[M];
void dfs2(int now,int top){
ltop[now]=top;
dfn[now]=++dfncnt;
rk[dfncnt]=now;
if(!hson[now])return;
dfs2(hson[now],top);
for(auto p:E[now])if(p^fa[now]&&p^hson[now])dfs2(p,p);
return;
}
inline int LCA(int u,int v){
while(ltop[u]!=ltop[v]){
if(dep[ltop[u]]>dep[ltop[v]])u=fa[ltop[u]];
else v=fa[ltop[v]];
}
if(dep[u]>dep[v])return v;
return u;
}
int lfa[M],afa[M][20];
vector<pUnit> preil[M],preol[M];
vector<int> Q,Q1;
inline void init(){
dfs1(1,0);
dfs2(1,1);
for(int i=1;i<=n;i++)Q.push_back(dep[i]);
int id=0,dlta=0,c1,c0;
while(!Q.empty()){
Q1.clear();
c1=0,c0=0;
for(auto p:Q)if(p&(1<<id))c1++;else c0++;
if(c0>c1){
dlta+=(1<<id);
for(auto p:Q)if(p&(1<<id))Q1.push_back(p+(1<<id));
}else for(auto p:Q)if(!(p&(1<<id)))Q1.push_back(p);
swap(Q,Q1);
}
for(int i,p=1,ppc,lbt;p<=n;p++){
i=rk[p];
dep[i]+=dlta;
lbt=(dep[i]&-dep[i]);
preil[i].resize(lbt+1);
preol[i].resize(ppc=__builtin_popcount(dep[i])+1);
preil[i][0]=make_pair(I,I);
int now=i;
for(int j=1;j<=lbt&&now;j++,now=fa[now])preil[i][j]=mer(preil[i][j-1],S[now]);
lfa[i]=now;preol[i][0]=make_pair(I,I);
now=i;
afa[i][0]=i;
for(int j=1;j<ppc&&now;j++,now=lfa[now])preol[i][j]=mer(preol[i][j-1],preil[now][(dep[now]&-dep[now])]),afa[i][j]=lfa[now];
}
return;
}
inline Unit query(int u,int v){
int lca=LCA(u,v);
int p,d,t;
Unit A,B;
A=I;B=I;
if(dep[u]!=dep[lca]){
p=__lg(dep[u]^dep[lca])+1;
d=(dep[u]>>p)<<p;t=max(0,__builtin_popcount(dep[u]^d)-1);
A=merge(A,preol[u][t].first);
A=merge(A,preil[afa[u][t]][(1<<(p-1))-(dep[lca]^d)].first);
}
A=merge(A,S[lca]);
if(dep[v]!=dep[lca]){
p=__lg(dep[v]^dep[lca])+1;
d=(dep[v]>>p)<<p;t=max(0,__builtin_popcount(dep[v]^d)-1);
B=preol[v][t].second;
B=merge(preil[afa[v][t]][(1<<(p-1))-(dep[lca]^d)].second,B);
}
return merge(A,B);
}
};
预处理常数可能比较大，但是确实需要卡常的可以自行取用。
P7624 [AHOI2021 初中组] 地铁
B 市的地铁历史悠久，小雪和小可可乘坐的 X 号线是环形路线，上面分布着 \(n\) 个车站，相邻两个车站之间的铁路长度为正整数。现在小雪进行了一些观察，得到了 \(m\) 条信息，第 \(i\) 条信息是如下形式之一：
- 环上顺时针由 \(S_i\) 到 \(T_i\) 的一段距离不小于一个给定的值 \(L_i\)（\(S_i\) 和 \(T_i\) 是两个车站）；
- 环上顺时针由 \(S_i\) 到 \(T_i\) 的一段距离不大于一个给定的值 \(L_i\)。
小雪想要你计算最后 X 线地铁的总长度有多少种不同的合法取值。
\(3 \le n \le 500\)，\(1 \le m \le 500\)，\(1 \le L_i \le 10^9\)。
看看我们的差分约束吧，我们好久没做了！事实上我们找的两道差分约束我都没做出来。废了。
首先一定断环为链，那么我们需要钦定环长。因为这个操作仅有不小于和不大于，所以答案一定是一个区间内的。
二分区间是天方夜谭，但是这个题有一些特殊的性质。考虑二分右端点。如果建出的图没有负环，那么右端点一定大于等于这里，如果有负环，并且负环上，环长的系数是正数，那么环长需要更大才行，所以右端点一定大于这里；这两种情况之外，右端点就一定小于等于这里。
知道右端点之后就知道左端点了。上面做的就是精细讨论二分判定时得到的信息。
然后就做完了。时间复杂度 \(O(nm\log V)\)。
P4926 [1007] 倍杀测量者
最傻逼的一集。
今天 Scarlet 在机房有幸目睹了一场别开生面的 OI 训练。因为一些奇妙的 SPJ，比赛中所有选手的得分都是正实数（甚至没有上限）。
当一位选手 A 的分数不小于选手 B 的分数 \(k\)（\(k>0\)）倍时，我们称选手 A \(k\) 倍杀 了选手 B，选手 B 被 选手 A \(k\) 倍杀 了。
更奇妙也更激动人心的是，训练前有不少选手立下了诸如 “我没 \(k\) 倍杀选手 X，我就女装”，“选手 Y 把我 \(k\) 倍杀，我就女装” 的 Flag。
知道真相的良心教练 Patchouli 为了维持机房秩序，放宽了选手们的 Flag 限制。Patchouli 设定了一个 正 常数 \(T\)，立下 “我没 \(k\) 倍杀选手 X 就女装” 的选手只要成功 \(k - T\) 倍杀了选手 X，就不需要女装。同样的，立下 “选手 Y 把我 \(k\) 倍杀我就女装” 的选手只要没有成功被选手 Y \(k+T\) 倍杀，也不需要女装。
提前知道了某些选手分数和具体 Flag 的 Scarlet 实在不忍心看到这么一次精彩比赛却没人女装，为了方便和 Patchouli 交易，Scarlet 想要确定最大的实数 \(T\) 使得赛后一定有选手收 Flag 女装。
\(1\leq n,s\leq 1000\)，\(1\leq A,B,C,t\leq n\)，\(1\leq k\leq 10\)，\(1\leq x\leq 10^9\)。保证输入中的 \(C\) 两两不同。
首先二分 \(T\)。
然后取对数建边。
完事。
注意我们连边的时候连不需要女装的边，这样有负环就是至少有一个人要女装。
[ABC261Ex] Game on Graph
最近都没睡好。
Takahashi 和 Aoki 正在一张 \(n\) 个点，\(m\) 条边的带权有向图上玩游戏。游戏规则如下：
- 有一颗最初在 \(s\) 点的棋子。双方轮流移动这颗棋子，Takahashi 先手。
- 每一次移动都可以使棋子从边的一端移动到另一端。如果无法移动，也就是不存在出边时，游戏结束。
- 定义一局游戏的得分为棋子移动路径上的边权之和。如果经过一条边多次，边权也计算多次。
Takahashi 想要最小化游戏的得分，但 Aoki 想要最大化得分。请输出在最优策略下游戏的最终得分。特别地，如果游戏无法结束，请输出
INFINITY。\(1\leq n\leq 2\times 10^5,0\leq m\leq 2\times 10^5\)。
倒着做。因为正着做显然 INFINITY 不可能判，而且这个最大正着也只能搜。
类似拓扑排序，最小的条件是只要有一个出度搞定，最大的条件是所有出度全部搞定。如果不能到 \((s,0)\)（\(0\) 是先手，否则后手）那么就是无限，因为 Aoki 可以到达一个不可能到 INFINITY 的状态。初始状态是不存在出边的点。
注意连反边就 OK。
