DP - 补
应某些人要求发出来了(
这应该是 24 年 3 月份结束编写的东西。
简介
动态规划常用于最优化或计数问题,通常要满足最优子结构(一个问题的答案可以由其子问题答案算出),无后效性(可以按某种顺序求解),子问题的重叠性(递归时可能会走到相同子问题)。
使用递归实现就是记忆化搜索,而如果我们能确定转移顺序那么我们就可以按顺序转移。
这一类问题通常考察思维,所以极其令我厌恶,通常是先设计一个状态,再想状态之间的转移,然后再优化。
背包
通常的问题形式是:
有 nn 类物品,物品有体积 v,有价值 w,需要满足一定限制的条件下选择物品是的价值和最大。大多数题目的限制都是提及综合不超过 m。
01 背包
这个背包的特殊之处在于每类物品只有一个。
为了防止一个物品多次选择,我们采用 从大到小枚举容积 的方式做。
转移方程明显为 fi,j←max(fi−1,j−v[i]+w),可滚。
完全背包
这种背包每类物品有无限个,这样就不用关心一个物品是否多次重复选择,我们容许多次选择,那么可以 从小到大枚举容积。
转移方程不变,可滚。
一种非常简单的优化是如果有 vi≥vj 且 wi≤wj,那么可以把种类 i 踢掉。那么一种更为简单的方式是,对于 v 相等的几类物品,只留下 w 最大的物品即可。
多重背包
这种背包每种物品的物品有 k 个。
首先可以二进制分组,把 k 拆分为 20+⋯+2p+q 的形式,前面 2 的几个幂就可以配出 1∼k−q 的所有情况,加上 q 就能配出 1∼k 的所有情况了,总物品数是 O(logk) 的,然后进行 01 背包。
也可以使用单调队列优化,此处先不提。
二维费用背包
多开一维记录状态即可。
分组背包
首先遍历每一组,内部首先从大到小枚举容量,再遍历每组中每个物品;外部遍历每个组即可。
板子题:P1757
// Problem: P1757 通天之分组背包
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1757
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-03 20:11:30
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<pair<int,int> > v[101];
int a,b,k,ans;
int dp[1001];
int main(){
ios::sync_with_stdio(0);
cin>>m>>n;
for(int i=1;i<=n;i++)cin>>a>>b>>k,v[k].push_back(make_pair(a,b));
for(int i=0;i<=100;i++){
for(int j=m;j>=0;j--){
for(auto p:v[i]){
if(j>=p.first)dp[j]=max(dp[j],dp[j-p.first]+p.second),ans=max(ans,dp[j]);
}
}
}
cout<<ans;
return 0;
}
例题
P4141 消失之物
考虑 01 背包没有对顺序的要求,所以每次都可以把现在要撤销的贡献都当成最后一次加入的,那么可以直接撤销。转移方程式:fi=fi+fi−w[j]。
// Problem: P4141 消失之物
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4141
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-03 20:43:35
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
int w[10001];
int dp[10001]={1};
int cnt[10001];
signed main(){
ios::sync_with_stdio(0);
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>w[i];
for(int i=1;i<=n;i++){
for(int j=m;j>=w[i];j--){
dp[j]+=dp[j-w[i]];
dp[j]%=10;
}
}
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++)cnt[j]=dp[j];
for(int j=w[i];j<=m;j++)cnt[j]-=cnt[j-w[i]];
for(int j=1;j<=m;j++)cout<<(cnt[j]%10+10)%10;
cout<<"\n";
}
return 0;
}
LOJ 6089
小 Y 有一个大小为 n 的背包,并且小 Y 有 n 种物品。
对于第 i 种物品,共有 i 个可以使用,并且对于每一个 i 物品,体积均为 i 。
求小 Y 把该背包装满的方案数为多少,答案对于 23333333 取模。
定义两种不同的方案为:当且仅当至少存在一种物品的使用数量不同。
考虑由于 i≥√n 时,可以发现每个物品都不可能选完,那么可以把这部分当做完全背包来做,所以我们根号分治来解决这个问题。
当 i<√n 时,由于是计数题,可以使用模意义下的前缀和优化多重背包。
当 i≥√n 时,我们把操作拆分成两类:第一种是加入一个体积为 ⌈√n⌉ 的物品,第二种是将所有物品的体积都加一,那么转移方程式就是 gi,j=gi−1,j−⌈√n⌉+gi,j−i。
最后把两边卷起来即可,时间复杂度 O(n√n)。
// Problem: #6089. 小 Y 的背包计数问题
// Contest: LibreOJ
// URL: https://loj.ac/p/6089
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-04 18:46:54
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,B;
const int mod=23333333;
int f[100001],sum[100001],gsum[100001];
int g[320][100001];
signed main(){
ios::sync_with_stdio(0);
cin>>n;
B=sqrt(n);
f[0]=1;
g[0][0]=1;
for(int i=1;i<=B;i++){
for(int j=0;j<i;j++)sum[j]=f[j];
for(int j=i;j<=n;j++)sum[j]=(sum[j-i]+f[j])%mod;
for(int j=n;j>=i;j--){
if(j>=i*(i+1))f[j]=(sum[j]-sum[j-(i+1)*i]+mod)%mod;
else f[j]=sum[j];
}
}
for(int i=1;i<=B;i++){
for(int j=B+1;j<=n;j++){
g[i][j]=(g[i-1][j-B-1]+g[i][j-i])%mod;
}
}
for(int j=0;j<=n;j++){
for(int i=0;i<=B;i++)
gsum[j]+=g[i][j],gsum[j]%=mod;
}
int ans=0;
for(int i=0;i<=n;i++)ans+=f[i]*gsum[n-i],ans%=mod;
cout<<ans;
return 0;
}
P8392 物品
神仙 dp 题。
考虑弱化一下数据范围,我们首先贪心地全选,记和为 s。如果 s>L,那么就从大到小删除物品直到 s∈[L−m,L];如果 s<L,那么从小到大删除物品直到 s∈[L−m,L],如果这一步不能满足那么直接无解。这样做能使得在下面的背包中保证最优而保证不会使状态重复。
接下来考虑调整。首先,我们对于接下来的调整,一定能找到一种调整的顺序,使得背包里的物品和在 [L−m,L+m] 之间,证明是简单的,当出现即将减出边界的时候,我们一定能在之后找到一个物品体积大于 0 的来回到 L 处,即将加出边界是一个道理。那么我们就证明了只可能有 2m+1 种状态有效,即存在只使用 ≤2m+1 次操作的方法进行调整。
那么极限情况下是减操作有 m 个,加操作有 m+1 个,背包值域开成 [−m2−m,m2+m] 跑一遍二进制分组优化多重背包即可。值域开成这样而不是 [−m2,m2] 是因为这样我感觉更严谨。
由于存在只用 ≤2m+1 次操作的方法进行调整,所以每个物品的个数最多有 2m+1 个,时间复杂度就是 O(m3logm)。
注意用于反悔的物品的添加和体积为负时完全背包是正着扫的。
// Problem: P8392 [BalticOI 2022 Day1] Uplifting Excursion
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P8392
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-05 09:35:09
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
#define int long long
using namespace std;
int used[1001],lef[1001];
int getid(int id){
return id+301;
}
void use(int id,int num){
used[getid(id)]+=num;
lef[getid(id)]-=num;
return;
}
void putb(int id,int num){
used[getid(id)]-=num;
lef[getid(id)]+=num;
return;
}
int w[1000005],V[1000005],dp[5000005],ans,obcnt;
long long sum[10001];
long long m,l;
int s;
void insertobj(int val,int num,int v){
// cout<<val<<" "<<num<<" "<<v<<"\n";
// if(v==-6)return;
if(num==0)return;
int ed=log2(num)-1,nows=0;
for(int o=0;o<=ed;o++){
nows+=(1ll<<o);
w[++obcnt]=val*(1ll<<o);
V[obcnt]=v*(1ll<<o);
}
// cout<<num<<" "<<nows<<"\n";
if(num==nows)return;
w[++obcnt]=val*(num-nows);
V[obcnt]=v*(num-nows);
return;
}
signed main(){
ios::sync_with_stdio(0);
cin>>m>>l;
for(int i=-m;i<=m;i++)cin>>sum[getid(i)],s+=sum[getid(i)]*i,use(i,sum[getid(i)]);
// cerr<<s<<"\n";
if(s>l){
int now=m;
while(s-sum[getid(now)]*now>l&&now>0)s-=sum[getid(now)]*now,putb(now,sum[getid(now)]),now--;
if(now==0){
cout<<"impossible";
exit(0);
}
int divi=(s-l+now-1)/now;
putb(now,divi);
s=s-now*divi;
}else if(s<l){
int now=-m;
while(s-sum[getid(now)]*now<l&&now<0)s-=sum[getid(now)]*now,putb(now,sum[getid(now)]),now++;
// cout<<s<<" "<<now<<"\n";
if(now==0){
cout<<"impossible";
exit(0);
}
int divi=(s-l)/now;
putb(now,divi);
s=s-now*divi;
}
for(int i=-m;i<=m;i++)ans+=used[getid(i)],lef[getid(i)]+=sum[getid(i)];
// cout<<s<<" "<<l<<"\n";
// for(int i=-m;i<=m;i++)cout<<used[getid(i)]<<" ";
int goal=l-s+m*m+m;
int pv=(m*m+m)*2;
for(int i=0;i<=pv;i++)dp[i]=-1e18;
dp[pv/2]=0;
for(int i=-m;i<=m;i++){
insertobj(-1,used[getid(i)],-i);
insertobj(1,lef[getid(i)],i);
}
for(int i=1;i<=obcnt;i++){
if(V[i]>0){
for(int j=pv;j>=V[i];j--){
dp[j]=max(dp[j],dp[j-V[i]]+w[i]);
}
}else{
for(int j=0;j<=pv+V[i];j++){
dp[j]=max(dp[j],dp[j-V[i]]+w[i]);
}
}
}
// cout<<dp[goal+6]<<"\n";
if(dp[goal]<-2*m-1)cout<<"impossible";
else cout<<(ans+dp[goal]);
return 0;
}
区间 dp
简介
区间 dp 通常使用 fl,r 作为状态,来解决 f1,n 的问题。使用区间 dp 通常是因为求解的问题在区间上,并且答案可以从它的子区间转移过来。转移通常是枚举分界点 mid,从 fl,mid−1 和 fmid,r 转移过来,有时候也会从 [l,r−1] 和 [l+1,r] 转移过来。
转移时通常先枚举区间长度,再枚举左端点,再枚举其他参数(如分界点)。需要找到一个合适的方法将区间分割成的两个合法的区间可以简单合并。
例题
P1880 石子合并
有一个显然的转移: fl,r=maxmid∈[l,r)(fl,mid+fmid+1,r)+∑ri=la[i]。
后面那部分使用前缀和,时间复杂度 O(n3),需要断环为链。
// Problem: P1880 [NOI1995] 石子合并
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1880
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-05 11:37:09
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
int n,dp[201][201],a[1001],s[1001];
int main(){
ios::sync_with_stdio(0);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i],a[i+n]=a[i];
for(int i=1;i<=2*n;i++)s[i]=s[i-1]+a[i];
for(int i=2;i<=n;i++){
for(int l=1;l<=2*n-i+1;l++){
int r=l+i-1;
for(int mid=l;mid<r;mid++){
dp[l][r]=max(dp[l][r],dp[l][mid]+dp[mid+1][r]);
}
dp[l][r]+=s[r]-s[l-1];
}
}
int maxx=0;
for(int i=1;i<=n;i++){
maxx=max(dp[i][i+n-1],maxx);
}
for(int i=2;i<=n;i++){
for(int l=1;l<=2*n-i+1;l++){
int r=l+i-1;
for(int mid=l;mid<r;mid++){
dp[l][r]=min(dp[l][r],dp[l][mid]+dp[mid+1][r]);
}
dp[l][r]+=s[r]-s[l-1];
}
}
int minn=1e9;
for(int i=1;i<=n;i++){
minn=min(dp[i][i+n-1],minn);
}
cout<<minn<<"\n"<<maxx;
return 0;
}
P5336 成绩单
首先想到设 fl,r 为区间 [l,r] 的最优答案,不难发现这样仍无法转移,因为一个区间中可能选出多个区间使得剩余区间被分成 O(n) 段。那么考虑我们直接暴力记录下剩余区间的最大最小值,则有状态 gl,r,mx,mi 表示区间 [l,r] 中选出若干区间后剩余区间的最大最小值为 mx 和 mi 时,之前选出区间的代价最小值。
首先,有 fl,r=mingl,r,mx,mi+b×(mx−mi)2+a。然后,我们再来思考如何转移 g 数组。
我们把问题抽象成如果 g 状态从右边又合并了一个元素时如何转移。
当新合并的元素 r+1 分到了剩余区间中,那么有 gl,r+1,max(w[r+1],mx),min(w[r+1],mi)=min(gl,r,mx,mi)。
当新合并的元素随区间 [k,r+1] 一起计算贡献时,有 gl,r+1,mx,mi=min(gi,k,mx,mi+fk+1,r+1)。显然这里目前只能当前区间的 mx,mi 内容,所以式子改写为 gl,r,mx,mi=min(g+i,k,mx,mi+fk+1,r)。
最后把 g 数组里的内容转移到 f 数组即可。
// Problem: P5336 [THUSC2016] 成绩单
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5336
// Memory Limit: 500 MB
// Time Limit: 2000 ms
// Start coding at 2024-01-05 18:02:52
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
int n;
int f[51][51],dp[52][52][52][52];
int d[51];
int w[51];
int a,b,tot;
int main(){
ios::sync_with_stdio(0);
cin>>n>>a>>b;
for(int i=1;i<=n;i++)cin>>d[i],w[i]=d[i];
for(int i=0;i<=n;i++)for(int j=0;j<=n;j++)f[i][j]=1e9;
for(int i=0;i<=n;i++)for(int j=0;j<=n;j++)for(int k=0;k<=n;k++)for(int o=0;o<=n;o++)dp[i][j][k][o]=1e9;
sort(d+1,d+n+1);
tot=unique(d+1,d+n+1)-d-1;
for(int i=1;i<=n;i++)w[i]=lower_bound(d+1,d+tot+1,w[i])-d,f[i][i]=a,dp[i][i][w[i]][w[i]]=0;
for(int len=1;len<=n;len++){
for(int l=1,r=len;r<=n;l++,r++){
for(int mx=1;mx<=tot;mx++){
for(int mi=1;mi<=mx;mi++){
int &t1=dp[l][r][mx][mi];
int &t2=dp[l][r+1][max(mx,w[r+1])][min(mi,w[r+1])];
for(int k=l;k<r;k++)t1=min(t1,dp[l][k][mx][mi]+f[k+1][r]);
t2=min(t2,t1);
f[l][r]=min(f[l][r],t1+a+b*(d[mx]-d[mi])*(d[mx]-d[mi]));
}
}
}
}
cout<<f[1][n];
return 0;
}
AGC035D Add and Remove
考虑不难发现原序列左右两端的数只可能被统计到一次,那么我们可以给序列内的所有数一种分配对答案进行多少次贡献的方案使答案最小。
考虑对于任意两点中间插入一个值为 ap 的元素,而左右两元素对答案的贡献次数是 xl 和 xr,那么中间这个元素对答案的贡献次数就是 xl+xr。
所以每次暴力枚举每个区间的端点,转移方程式为 fl,r,xl,xr=minl<i<r(fl,i,xl,xl+xr+fi,r,xl+xr,xr+ai×(xl+xr)),其中,当 r−l=1 时,不难发现所有贡献都已在之前的递归统计完毕,值为 0。
使用 dfs 实现。
// Problem: [AGC035D] Add and Remove
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/AT_agc035_d
// Memory Limit: 1 MB
// Time Limit: 2000 ms
// Start coding at 2024-01-05 20:26:39
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
#define int long long
using namespace std;
int a[21],n;
int dfs(int l,int r,int cntl,int cntr){
if(r-l==1)return 0;
int res=1e18;
for(int i=l+1;i<=r-1;i++)res=min(res,dfs(l,i,cntl,cntl+cntr)+dfs(i,r,cntl+cntr,cntr)+a[i]*(cntl+cntr));
return res;
}
signed main(){
ios::sync_with_stdio(0);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
cout<<dfs(1,n,1,1)+a[1]+a[n];
return 0;
}
留了一道 AGC039E 没补,因为感觉太抽象了。
树形 dp
简介
通常维护子树内的信息,然后在父亲处被遍历到然后转移。有些时候会求不同根的答案从而需要换根 dp。
TQX 给的例题太毒瘤了,之后再找几道。
数位 dp
简介
关键在于看出题目需要逐位进行 dp。
一般需要单独处理卡上界的情况,可以将卡上界作为一个状态,也可以把上界直接拆开。有时同时有上下界时需要转化成前缀和相减。
例题
P2657 windy 数
数位 dp 板子题。
首先我们定义状态 fi,j 是最高位为 j 的 i 位数中,有多少个数是 windy 数。这个易求,稍微拆一下式子可得:
由此我们对于任意 fi,j,可以枚举每位的数判断转移是否合法,然后从 fi−1,k 转移过来。
这一步的代码实现:
int f[21][21];
void prework(){
for(int i=0;i<10;i++)f[1][i]=1;
for(int i=2;i<=10;i++){
for(int j=0;j<10;j++){
for(int k=0;k<10;k++){
if(abs(j-k)>1)f[i][j]+=f[i-1][k];
}
}
}
return;
}
这时我们来拆贡献,以询问上界 2952 为例。
根据 f 的定义,计算 0∼1999 时,需要计算 0∼9,10∼99,100∼999,1000∼1999,极其复杂,所以我们另外定义一个数组 pf,来计算 0∼9⋯9 的 windy 数个数。而为什么不能直接用 f4,0 计算 0∼999 呢,因为 f4,0 是针对于 0000∼0999 计算的,是带前导 0 的。
这个 pf 可以在 prework() 中一同处理出来。因为不难发现 pfi=pfi−1+∑9j=1fi,j。
int f[21][21],pf[21];
void prework(){
for(int i=0;i<10;i++)f[1][i]=1;
pf[0]=1,pf[1]=10;
for(int i=2;i<=10;i++){
for(int j=0;j<10;j++){
for(int k=0;k<10;k++){
if(abs(j-k)>1)f[i][j]+=f[i-1][k];
}
}
pf[i]=pf[i-1];
for(int j=1;j<10;j++)pf[i]+=f[i][j];
}
return;
}
这个时候就完全可以拆开 2952 这个数了。
当然,有些较特殊的数,比如 2377,算了 0∼2299 之后就不能算了,因为这个时候出现了固定的两位不合法的情况,无论后面填什么,这个数都会不合法。
那么可以依照拆的这个思路写出代码:
int tmp[11];
int calc(int x){
int org=x,cnt=0,res=0;
while(org){tmp[++cnt]=org%10,org/=10;}
res=pf[cnt-1];
for(int i=1;i<tmp[cnt];i++)res+=f[cnt][i];
for(int i=cnt-1;i>0;i--){
for(int j=0;j<tmp[i];j++){
if(abs(j,tmp[i+1])>1)res+=f[i][j];
}
if(abs(tmp[i+1]-tmp[i])<2)break;
}
return res;
}
不难发现这份代码只求了 0∼2951 的数,因为再处理一遍 2952 需要添加较多代码,为了精简省去了这些特判。
完整代码:
// Problem: P2657 [SCOI2009] windy 数
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2657
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-08 21:11:00
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
int f[21][21],pf[21],tmp[11];
void prework(){
for(int i=0;i<10;i++)f[1][i]=1;
pf[0]=1;
pf[1]=10;
for(int i=2;i<=10;i++){
for(int j=0;j<10;j++){
for(int k=0;k<10;k++){
if(abs(j-k)>1)f[i][j]+=f[i-1][k];
}
}
pf[i]=pf[i-1];
for(int j=1;j<10;j++)pf[i]+=f[i][j];
}
return;
}
int calc(int x){
int cnt=0,res=0;
while(x){
tmp[++cnt]=x%10;
x/=10;
}
res=pf[cnt-1];
for(int i=1;i<tmp[cnt];i++)res+=f[cnt][i];
for(int i=cnt-1;i>=1;i--){
for(int j=0;j<tmp[i];j++){
if(abs(j-tmp[i+1])>1)res+=f[i][j];
}
if(abs(tmp[i+1]-tmp[i])<2)break;
}
return res;
}
int l,r;
int main(){
ios::sync_with_stdio(0);
cin>>l>>r;
prework();
cout<<calc(r+1)-calc(l)<<"\n";
return 0;
}
P4999 烦人的数学作业
同样定义 fi,j 为第 i 位首位为 j 时的答案,同样可以转移:fi,j=∑9k=0fi−1,k+10i−1×j。
并且统计答案时不需要判断什么,较为简单。
// Problem: P4999 烦人的数学作业
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4999
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-09 20:14:44
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=1e9+7;
int f[21][21],_10[21]={1};
void prework(){
for(int i=0;i<10;i++)f[1][i]=i;
for(int i=2;i<=19;i++){
for(int j=0;j<10;j++){
for(int k=0;k<10;k++){
(f[i][j]+=f[i-1][k])%=mod;
}
f[i][j]+=_10[i-1]*j%mod;
f[i][j]%=mod;
}
}
return;
}
int T,l,r;
int tmp[21];
int calc(int x){
int res=0,cnt=0;
while(x){
tmp[++cnt]=x%10;
x/=10;
}
int nowsum=0;
for(int i=cnt;i>=1;i--){
for(int j=0;j<tmp[i];j++)res=(res+f[i][j])%mod;
res=(res+_10[i-1]*nowsum%mod*tmp[i]%mod)%mod;
nowsum+=tmp[i];
}
return res;
}
signed main(){
ios::sync_with_stdio(0);
for(int i=1;i<=20;i++)_10[i]=_10[i-1]*10%mod;
cin>>T;
prework();
while(T--){
cin>>l>>r;
cout<<(calc(r+1)-calc(l)+mod)%mod<<"\n";
}
return 0;
}
P2602 数字计数
考虑定义一个结构体存每个数字的出现次数,然后按 P2657 的方式转移即可。
// Problem: P2602 [ZJOI2010] 数字计数
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2602
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-09 20:48:19
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
#define int long long
struct an{
int cnt[10];
an operator + (const an &a) const{
an res;
for(int i=0;i<10;i++)res.cnt[i]=cnt[i]+a.cnt[i];
return res;
}
an operator - (const an &a) const{
an res;
for(int i=0;i<10;i++)res.cnt[i]=cnt[i]-a.cnt[i];
return res;
}
void print(){
for(int i=0;i<10;i++)cout<<cnt[i]<<" ";
cout<<"\n";
return;
}
void init(){
for(int i=0;i<10;i++)cnt[i]=0;
return;
}
}f[21][21],pf[21];
int _10[21]={1};
void prework(){
for(int i=0;i<10;i++)f[1][i].cnt[i]++;
pf[0].cnt[0]++;
for(int i=0;i<10;i++)pf[1].cnt[i]++;
for(int i=2;i<=20;i++){
for(int j=0;j<10;j++){
for(int k=0;k<10;k++){
f[i][j]=f[i][j]+f[i-1][k];
}
f[i][j].cnt[j]+=_10[i-1];
// f[i][j].print();
}
pf[i]=pf[i-1];
for(int j=1;j<10;j++)pf[i]=pf[i]+f[i][j];
}
return;
}
int tmp[21];
an calc(int x){
an res;
res.init();
int cnt=0,org=x;
while(x){
tmp[++cnt]=x%10;
x/=10;
}
res=res+pf[cnt-1];
for(int i=1;i<tmp[cnt];i++)res=res+f[cnt][i];
org-=tmp[cnt]*_10[cnt-1];
for(int i=cnt-1;i>=1;i--){
res.cnt[tmp[i+1]]+=org;
for(int j=0;j<tmp[i];j++)res=res+f[i][j];
org-=tmp[i]*_10[i-1];
}
return res;
}
signed main(){
ios::sync_with_stdio(0);
for(int i=1;i<=18;i++)_10[i]=_10[i-1]*10;
prework();
int l,r;
cin>>l>>r;
(calc(r+1)-calc(l)).print();
return 0;
}
UOJ140【UER #4】被粉碎的数字
TQX 的题解省去了好多细节。
考虑仍然使用数位 dp 解决。我们来分析一下什么状态时必要的。
数位 dp 的通常转移方式是从低位到高位转移,于是对于每一位要乘 k 来讲,我们要统计这一位像下一位进了多少位,还要统计到这一位了,f(x) 与 f(kx) 之间的差是多少。最重要的是,因为 1≤x≤R,我们要保证 x 在范围内的话,我们就要再记录一个 当前位 x 是否超出 R 的边界 ,即 xcur 与 Rcur 的关系,当 xi=Ri 时,nxtlim 不变,即和准备转移过来的 lim 一致。转移的时候就两边分别转移即可。
// Problem: #140. 【UER #4】被粉碎的数字
// Contest: UOJ
// URL: https://uoj.ac/problem/140
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-10 15:37:35
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
#define int long long
int dp[31][411][1011][2];
int R,k,cnt;
int tmp[31];
signed main(){
ios::sync_with_stdio(0);
cin>>R>>k;
while(R){
tmp[++cnt]=R%10;
R/=10;
}
cnt+=3;//k<=1000
dp[0][200][0][0]=1;
for(int i=0;i<cnt;i++){
for(int j=0;j<=400;j++){
for(int h=0;h<=999;h++){
for(int lim=0;lim<=1;lim++){
for(int x=0;x<10;x++){
int nxtlim=(tmp[i+1]==x?lim:(tmp[i+1]<x));
dp[i+1][j+x-(k*x+h)%10][(k*x+h)/10][nxtlim]+=dp[i][j][h][lim];
}
}
}
}
}
cout<<dp[cnt][200][0][0]-1;
return 0;
}
恶补数位 dp。剩余的题详见 Problem_unruled_record。
状压 dp
简介
就是 dp 的时候出现了若干维,但是值域都很小(大多是选择是或不是),这个时候可以用进制压位。多数情况是压到 2n,可能会与 meet in middle 或者什么 FWT 一起用,也出现在数据分治时用。
例题
P1879 Corn Fields
设状态 fi,j 为前 i 行,第 i 行状态为 j 时的方案数。不难发现每一行选择哪些种草的状态能压到一个 int 里。以此作为状态,暴力枚举上一行和这一行的所有状态然后转移即可。时间复杂度 O(n22n)。
// Problem: P1879 [USACO06NOV] Corn Fields G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1879
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-11 19:38:31
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
const int mod=1e8;
int f[13][(1<<12)];
int n,m;
int g[13];
bool te[(1<<12)];
int tt;
int main(){
ios::sync_with_stdio(0);
cin>>m>>n;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
cin>>tt;
g[i]+=(tt<<(n-j));
}
}
for(int i=0;i<(1<<12);i++){
te[i]=1;
for(int j=1;j<12;j++)if(((i>>j)&1)&&((i>>(j-1))&1))te[i]=0;
}
f[0][0]=1;
for(int i=1;i<=m;i++){
for(int j=0;j<(1<<n);j++){
for(int k=0;k<(1<<n);k++){
if(!f[i-1][k])continue;
if(te[j]&&((((1<<n)-1)^k)&g[i]&j)==j)(f[i][j]+=f[i-1][k])%=mod;
}
}
}
int ans=0;
for(int i=0;i<=(1<<n)-1;i++)(ans+=f[m][i])%=mod;
cout<<ans;
return 0;
}
P3204 [HNOI2010] 公交线路
题解真的是没有一个是真正讲清楚了的。
考虑根据限制,我们可以转化一下贡献:即在任意一个 [i,i+p−1] 的区间内,一定存在一个子序列是 [1,K] 的排列。
我们设距离 i 最近的且在区间 [i,i+p−1] 内的 [1,K] 之间的数为有效状态,那么这里就能使用 0/1 状压,考虑如何转移。
首先不难发现,我们转移的对象就是删掉首位元素,然后再末尾补一个 0 后的数。
我们举个例子:p=5,K=3 时,假如有状态 10110,那么第二个 0 必须被前面的 1 转移,即 10110→11100。而如果有状态 11001,那么第一位实际上能转移到剩下的任何一个 0 的位置上,于是有 11001→10110 和 11001→11010 和 11001→10011。
从上面两个例子来看其实我们能枚举每一个数然后枚举每个操作后的 0,在 O(p×2p) 的时间复杂度内完成转移的构建。
看到 N≤109 的数据范围,想到矩阵转移,上面的转移明显是一个 dpi,j=∑kdpi−1,k 的形式,直接构建转移矩阵然后转移即可。这个地方不难发现上面的所有状态的首位都是 1,然后我们离散化一下,状态数为 (P−1K−1),最大状态数为 (95)=126,设 k=126,时间复杂度为 O(k3logN+p2p),可以通过。
DP 的优化
数据结构优化 DP
单调队列优化 DP
首先复习一下单调队列。
单调队列就是维护一个双端队列,保证队内元素降序,每次移动区间时如果这个数的最大值就是弹出的数,那么就弹出这个下标,然后加入末尾的数。加入时保证序列内元素值有序。
而单调队列优化 DP 就是 fi 可以从 maxl≤k≤r(fk) 转移过来,并且 l,r 均单调不减时,可以使用单调队列优化。如果保证 l=1,那么左侧不用弹出,可以使用单调栈维护。
Slope Trick
非常难以理解的用堆维护的优化 DP 方式。
考虑我们现在得到了一个 DP 转移方程式 fi,j=⋯,并且可以用数学归纳法证明 fi,∗ 是有凸性并且是一次分段函数,如果该函数的所有斜率都能用整数表示,我们可以考虑使用记录拐点和最右侧无限延伸的一条射线的方式来来记录整个凸壳。假如说该拐点的左右两端的一次函数斜率相差为 p,那么就在此处放 p 个相同的拐点坐标来记录。
设凸函数 C 的拐点集合为 S,直线为 f,那么合并 C1,C2 到 C 处则需要进行 S=S1∪S2,f=f1+f2(斜率相加,截距相加)。
显然可以用可并堆可以轻松维护。当然,每道题有不同的转移方式,就会有不同的合并方式,比如可能需要弹出某些元素再进行合并等。
其他数据结构优化 DP
使用我们熟知的线段树、树状数组等结构,可以用来处理一些区间转移或者类似
转移的 dp。基本上重点是在数据结构上,这里不多赘述。——TQX 课件
例题
Slope Trick 较为难懂,所以可能很大篇幅在说这个。
CF713C Sonya and Problem Wihtout a Legend
(这个题目名打错了吗?)
设 fi,j 为第 i 个位置填 j 时达成 严格递增 的最小代价,不难发现转移方程式:
但是 ai≤109 的数据显然不允许我们用这个转移方程式转移,所以我们考虑离散化后怎么做。
首先我们不难发现此时 非降 很好做,此时:
并且满足离散化,因为最优情况下就是把这个数变到某个数一样的位置,这样给后面的空间最大,并且代价最小。
那么考虑如何把 严格递增 转化成 非降。
我们如果将 ai 减去 i,我们就能将严格递增变为非降,因为我们达成了 非降 时的最优时,我们加上 i 就能保证严格递增,显然此时非降算出来的答案一定最优,因为此时相邻两数的差都扩大了 1,而我们之前转移时都是转移到已知的数上。
这个时候我们已经有 O(n2) 的做法了。但是这个做法并不优秀,我们可以考虑优化。
其实看到 min 和绝对值我们就已经可以想到凸性了。
考虑把 fi,j 改写为一个分段函数 fi(j)。不难发现 mink≤j(fi−1(k)) 一定是随 j 的增大递减的,而 \absai−j 是随着 j 的增大先递减后递增的。所以 fi 这个函数一定是下凸的。用数学归纳法可以证明 fi 函数的图像连续,即每两段函数之间均仅有一个拐点。
由于只需维护 min 值,所以我们没有必要维护右侧递增的凸壳,只需维护左侧递减的凸壳即可。而 \absai−j 是一个一次函数,所以我们每次只用添加两个 ai 的拐点。因为每次我们加入的点有 2 个,所以如果我们加入的点在最大的点之前,我们一定会把最后一段斜率为 0 的一段变成斜率为 1 的一段,此时要删除最大的拐点;
而加入第一个点是将该点之前的所有线段斜率减 1,加入第二个点是将该点之前的所有线段斜率加 1,所以当我们加入第二个点时统计答案。由于其右侧所有直线的斜率都增加 1,所以答案的增量就是该点与该点未加入时集合中的最大值的差。
如果我们加入的点在最大的点之后,我们显然只用加一个点就行了,因为另外那个点会被删掉。
// Problem: Sonya and Problem Wihtout a Legend
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF713C
// Memory Limit: 250 MB
// Time Limit: 5000 ms
// Start coding at 2024-01-15 09:14:47
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
// #define int long long
priority_queue<int> q;
int main(){
ios::sync_with_stdio(0);
int n,a;
long long ans=0;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a;
a-=i;
q.push(a);
if(a<q.top())q.push(a),ans+=q.top()-a,q.pop();
}
cout<<ans;
return 0;
}
求方案:P4331
考虑首先记录下每次的 min 值所在下标 ai。不难发现,当加入的数小于当前最大值,min 值对应下标变小,否则 min 值对应下标变大。
考虑我们模拟一下这个过程,把原序列看成 O(n) 个非降序列和 O(n) 个非升序列,那么假设有:
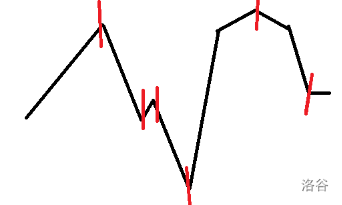
作为原序列值的走向,那么有:
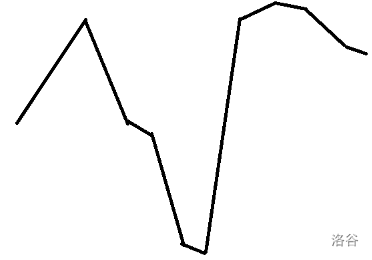
作为其 min 值走向。
观察可得,每次删除等于是在与前面所有拐点的中位数(或:平衡状态)靠近,而加入一个最大值就是纯加入一个最大值。
显然我们对于一段先升后降的函数取其中位数一定不劣,并且在中位数附近微调确实能做到最优。所以我们不难得到式子 ai←min(ai,ai+1),因为每次 ai 每次都最靠近平衡时的的最优情况,而 ai 单调递增时此时原序列一定单调递增,不改一定最优。这样做就能保证该不该时就不改,该平衡时平衡。
// Problem: P4331 [BalticOI 2004] Sequence 数字序列
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4331
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-15 11:44:23
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
int a[1000001];
priority_queue<int> q;
int x,n;
long long ans;
int main(){
ios::sync_with_stdio(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>x;
x-=i;
q.push(x);
if(x<q.top())q.push(x),ans+=q.top()-x,q.pop();
a[i]=q.top();
}
for(int i=n-1;i>=1;i--)a[i]=min(a[i],a[i+1]);
cout<<ans<<"\n";
for(int i=1;i<=n;i++)cout<<a[i]+i<<" ";
return 0;
}
P3642 [APIO2016] 烟火表演
前置知识是可并堆,这个数据结构在我的数据结构学习笔记还没有提到,之后会补(毕竟 dp -> 数学 -> 图论(树论) -> ds -> 贪心 -> 字符串续 -> GEO -> 博弈)。
考虑设 fi,j 为 i 点点燃后 j 时刻其子树内所有烟花全部同时点燃所需要花费的最小代价。首先有一般树形 DP 方程式:
看样子是 函数至点 的一个转移。但是对于每个点,由于 j 每次增量固定为 1,所以其实还是可以从 函数至函数 转移。同样的,这个函数能用数学归纳法证明其为下凸函数,并且适用于 Slope Trick。
首先考虑原函数 fi(x) 整体加上一个数 k 后的改变,首先这个函数会变成 g(x+k),然后所有值均向上移 k。因为加上 k 代表此时并不是 x 时刻时全部被点燃,而是 x+k 时刻时全部被点燃。那么对于拐点集合,加上一个数 k 就代表所有拐点全部向右移动 k。下面就可以开始分讨了。设 L,R 为函数 fv 斜率为 0 一段的左右端点。
对于 x<L 时,往右移动函数代表询问点向左移动,一定不优,所以我们干脆就不加任何数,所以 fi(x)=fv(x)+wi,v。
对于 L≤x<L+wi,v 时,询问点向左移动最多到 L 之后再想向左移一定不优,所以移动到 L 就要停止,这时移动量为 x−L,那么 fi(x)=fv(L)+(wi,v−(x−L))。
对于 L+wi,v≤x<R+wi,v,此时询问点左移 wi,v 一定在 [L,R] 间。那么不需要任何修改即可, fi(x)=fv(L)。
对于 x≥R+wi,v 时,此时询问点显然一直左移到 R 一定不劣,而只移动 wi,v 是不够的,所以要加长导火索。有 fi(x)=fv(L)+(x−R−wi,v)。
我们一个函数一个函数的看。
对于 fi(x)=fv(x)+wi,v,将原函数向上移动 wi,v 即可。
对与 fi(x)=fv(L)+(wi,v−(x−L)),不难发现 fi(x) 随 x 的增大而减小。因此我们要添加一段 [L,L+wi,v] 的斜率为 −1 的一段,这一段和原来之前函数的一段斜率为 −1 的一段正好接上,所以仅对于这个操作而言,我们可以删去 L 的拐点并且添加上一个 L+wi,v 的拐点。
对于 fi(x)=fv(L),就是把 [L,R] 这段斜率为 0 的部分平移到 [L+wi,v,R+wi,v] 上,此时根据前面两段的分析,我们不难发现此时这两段高度相同。所以我们删去 R 这个拐点,并添加 R+wi,v 这个拐点。
最后,对于 fi(x)=fv(L)+(x−R−wi,v),不难发现这个函数斜率为 1,而根据之前三个函数的拐点添加与删除,如果我们删除之前函数 ≥R 的所有拐点,我们就能保证最后这个函数斜率一直为 1。
总结一下,我们删除原函数 >L 的所有拐点并删除一次 L 本身,然后添加 L+wi,v,R+wi,v 两个拐点。我们就做好了我们合并到下一个函数的准备工作。
考虑如何找到 L。对于一个函数,他的儿子处理后一定会有一个斜率为 1 的直线,也就是说,在找 L 时,其凸壳最大斜率为 cntson。那么我们就需要弹出 cntson−1 个最大的拐点就能找到 R,弹出 R 之后就能找到 L。使用可并大根堆维护。
最后就是讨论如何得到答案。首先有 f1,0=∑i,jwi,j。然后我们可以锁定 L,然后一直弹出并在 f1,0 中删除拐点的下标值直到拐点集合为空,最后得到的值就是 f1,L。我们可以这样理解这个问题:我们正着想一下这个过程,设拐点集合大小为 S,那么最大斜率为 S。我们删除最小的拐点下标代表我们再继续删 S−1 次这个下标,删除次小的代表我们会继续删 S−2 次次小与最小的下标值差。这样正好和斜率导致的减量对应。
// Problem: P3642 [APIO2016] 烟火表演
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3642
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-15 19:45:06
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
long long val[600005];
int ch[600005][2],rt[300005],pa[300005];
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
int cnt;
int addP(long long x){
val[++cnt]=x;
return cnt;
}
int merge(int x,int y){
if(!x||!y)return x+y;
if(val[x]<val[y])swap(x,y);
int op=rnd()&1;
ch[x][op]=merge(ch[x][op],y);
return x;
}
void pop(int x){
// cerr<<x<<" "<<rt[x]<<" "<<ch[x][0]<<" "<<ch[x][1]<<"\n";
rt[x]=merge(ch[rt[x]][0],ch[rt[x]][1]);
return;
}
int n,m;
int x,y,degs[300005],w[300005];
long long ans;
int main(){
ios::sync_with_stdio(0);
cin>>n>>m;
for(int i=2;i<=n+m;i++){
cin>>x>>y;
pa[i]=x;
degs[x]++;
w[i]=y;
ans+=w[i];
}
for(int i=n+m;i>=2;i--){
// cerr<<i<<" now dealing\n";
for(int j=1;j<=degs[i]-1;j++)pop(i);
long long R=val[rt[i]];pop(i);
long long L=val[rt[i]];pop(i);
rt[i]=merge(rt[i],merge(addP(L+w[i]),addP(R+w[i])));
rt[pa[i]]=merge(rt[pa[i]],rt[i]);
}
while(degs[1]--)pop(1);//,cerr<<degs[1]<<"\n";
// cerr<<"\n";
while(rt[1])ans-=val[rt[1]],pop(1);
cout<<ans;
return 0;
}
还有部分 Slope Trick 的题待补。
P2627 [USACO11OPEN] Mowing the Lawn G
考虑一般 dp 方程式。设 fi,j 为选到第 i 个,此时不选第 i 个的最大贡献。有:
观察式子可以发现把 fi−p−prei−p 单调队列优化掉。时间复杂度 O(n)。
// Problem: P2627 [USACO11OPEN] Mowing the Lawn G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2627
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-17 18:11:05
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
long long dp[100005],E[100005];
int n,k;
deque<long long> q;
int main(){
ios::sync_with_stdio(0);
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>E[i],E[i]+=E[i-1];
E[n+1]=E[n];
// for(int i=1;i<=n+1;i++){
// for(int j=max(0,i-k-1);j<=i-1;j++){
// dp[i]=max(dp[i],dp[j]+E[i-1]-E[j]);
// }
// }
// cout<<dp[n+1];
q.push_back(0);
for(int i=1;i<=n+1;i++){
if(q.front()+k+1<i)q.pop_front();
dp[i]=dp[q.front()]+E[i-1]-E[q.front()];
while(!q.empty()&&dp[i]-E[i]>dp[q.back()]-E[q.back()])q.pop_back();
q.push_back(i);
}
cout<<dp[n+1];
return 0;
}
P2569 [SCOI2010] 股票交易
考虑列出朴素 dp 方程式:
发现是一个 O(n4) 的 dp,用单调队列优化 p 一维可以优化到 O(n3)。
考虑重构 dp 方程式,提前优化掉一维。不难发现我们可以添加一条 dpi,j=max(dpi,j,dpi−1,j)。这一条就严格保证了 dpi,j 是在前 i 个最优的,而不是第 i 个最优的。那么在上面的 dp 方程式中,我们有 p=i−W−1。
发现我们可以单调队列优化 k 一维,扫两次,单调队列比较的值是 bpi×k 或 api×k 加上 dpi−W−1,k,因为 −bpi×j 或 −api×j 是可以提出 max 函数内的。
代码像坨史。
// Problem: P2569 [SCOI2010] 股票交易
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2569
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-18 20:02:52
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
deque<int> q[2005][2];
int dp[2005][2005];
int n,maxp,W;
int ap[2005],bp[2005],as[2005],bs[2005];
int main(){
ios::sync_with_stdio(0);
cin>>n>>maxp>>W;
for(int i=1;i<=n;i++)cin>>ap[i]>>bp[i]>>as[i]>>bs[i];
for(int i=0;i<=n;i++){
for(int j=0;j<=maxp;j++){
dp[i][j]=INT_MIN+1e9;
}
}
dp[0][0]=0;
for(int i=1;i<=W;i++){
dp[i][0]=0;
for(int j=1;j<=maxp;j++){
if(j<=as[i])dp[i][j]=-ap[i]*j;
dp[i][j]=max(dp[i-1][j],dp[i][j]);
}
}
for(int i=W+1;i<=n;i++){
// cerr<<i<<"\n";
for(int j=0;j<=maxp;j++)dp[i][j]=dp[i-1][j];
for(int j=0;j<=maxp+bs[i]-1;j++){
// cerr<<j<<" in1\n";
if(!q[i][0].empty()&&q[i][0].front()<=j-bs[i])q[i][0].pop_front();
if(j<=maxp){
while(!q[i][0].empty()
&& dp[i-W-1][q[i][0].back()]
+ bp[i]*q[i][0].back()
< dp[i-W-1][j]
+ bp[i]*j)
q[i][0].pop_back();
q[i][0].push_back(j);
}
if(j>=bs[i])dp[i][j-bs[i]]=max(dp[i][j-bs[i]],
dp[i-W-1][q[i][0].front()]+bp[i]*(q[i][0].front()-(j-bs[i])));
}
// cerr<<"end\n";
for(int j=0;j<maxp;j++){
if(!q[i][1].empty()&&q[i][1].front()<=j-as[i])q[i][1].pop_front();
while(!q[i][1].empty()
&& dp[i-W-1][q[i][1].back()]
+ ap[i]*q[i][1].back()
< dp[i-W-1][j]
+ ap[i]*j)
q[i][1].pop_back();
q[i][1].push_back(j);
dp[i][j+1]=max(dp[i][j+1],
dp[i-W-1][q[i][1].front()]+ap[i]*(q[i][1].front()-(j+1)));
}
}
// for(int i=0;i<=n;i++){
// for(int j=0;j<=maxp;j++){
// cout<<dp[i][j]<<" ";
// }
// cout<<"\n";
// }
cout<<dp[n][0];
return 0;
}
CF939F Cutlet
比较好的一道 DP 题。
不难发现暴力转移:设 dpi,j,k 是第 i 个时刻最开始朝上那一面煎了 j 秒,目前正在煎第 k 面。当 i∈[lp,rp] 时有转移:
考虑优化这个 DP。
首先,后面的 j,k 可以压成只有 j。状态为目前朝上的一面煎了 j 秒。由于 O(nk) 的复杂度可过,我们就把第一个状态 i 改成 O(k) 级别的,于是设 dpi,j 为第 i 个区间的右端点时朝上的一面已经煎了 j 秒的最小翻转次数。
显然,一个区间有三种选择,即翻转 0,1,2 次,这里分开讨论。
- 当翻转 0 次时,正面朝上的那面被煎秒数不变,有:
- 当翻转 1 次时,我们把之前煎的过程抽象成先煎了 j′ 秒目前朝上的一面,然后一直煎现在煎的这一面,然后在当前区间转回去了。设转回去一共 k 秒,那么有 dpi,ri−(j′+k)←dpi,j′+1,令 j=ri−(j′+k),那么有 j′=ri−j−k,有如下转移:
- 当翻转 2 次时,同样将之前煎的过程抽象成先煎了 j′ 秒目前朝上的一面,那么翻转两次等同于朝上的一面不变,那么有 dpi,j′+k←dpi−1,j′+2。令 j=j′+k,那么有转移:
对于翻转一次时,由于 ri−j−k≤ri−1,那么就有 j+k≥ri−ri−1。而 k≤ri−li,所以有 j≥li−ri−1。然后我们就直接讨论最极端情况 j=0,我们发现 ri−j−(ri−li)=li>ri−1,此时 dpi−1,ri−k 一定是 +∞。其他情况手推也可发现直接计算是对答案没有影响的。
那么直接上单调队列优化 DP 即可。
// Problem: F. Cutlet
// Contest: Codeforces - Codeforces Round 464 (Div. 2)
// URL: https://codeforces.com/problemset/problem/939/F
// Memory Limit: 256 MB
// Time Limit: 4000 ms
// Start coding at 2024-01-22 16:32:33
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
int n,k;
int l,r;
int dp[101][200005];
deque<int> q;
void clear(){
while(!q.empty())q.pop_back();
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k;
for(int i=1;i<=2*n;i++)dp[0][i]=1e9;
dp[0][0]=0;
for(int i=1;i<=k;i++){
cin>>l>>r;
clear();
for(int j=0;j<=2*n;j++)dp[i][j]=dp[i-1][j];
//change 2 times
q.push_back(0);
int len=r-l;
for(int j=1;j<=r;j++){
if(!q.empty()&&q.front()<j-len)q.pop_front();
while(!q.empty()&&dp[i-1][q.back()]>dp[i-1][j])q.pop_back();
q.push_back(j);
dp[i][j]=min(dp[i][j],dp[i-1][q.front()]+2);
}
clear();
//change 1 time
for(int ri_j=0;ri_j<=r;ri_j++){
int j=r-ri_j;
if(!q.empty()&&q.front()<ri_j-len)q.pop_front();
while(!q.empty()&&dp[i-1][q.back()]>dp[i-1][ri_j])q.pop_back();
q.push_back(ri_j);
dp[i][j]=min(dp[i][j],dp[i-1][q.front()]+1);
}
}
if(dp[k][n]>=1e9)cout<<"Hungry";
else cout<<"Full\n"<<dp[k][n];
return 0;
}
P9871 [NOIP2023] 天天爱打卡
最近考的一道线段树优化 dp。
继承上一题的思路,我们离散化左右端点。设 dpi,j 时此时为第 i 个状态,而前面已经连续选了 j 个状态极其其中的区间了。
一个 trival 的思路是我们把每一个端点都设成状态,然后再把中间的区间设为状态。我们发现我们有 dpi,j←dpi−1,j−1−d×len,那么我们就可以把之前的所有状态倒置加入,省去区间平移,这样可以把这个操作转化为区间加,而对于吃饭的操作也能转化成区间加。我们每次在线段树开头加一个状态,表示此时我们只选当前状态的代价。这样每次二分出 k 步之前新建的线段树节点就能维护了,加状态需要询问区间最大值。
写完之后发现 T 了,被卡常了。其实不难发现可以把中间区间的状态压掉。那么我们每次先更新 dpi,0,再进行修改与吃饭操作即可。也可以最后更新 dpi+1,0,这是一个道理。注意更新时要特判两状态相邻,因为这个时候更新 dpi+1,0 不能从 dpi,0 更新,而是从更前面的状态的 dpi−1,0 转移,否则无法满足 不能连续超过 K 次打卡。
非常难调。而且压完状态也被卡常了。
// Problem: P9871 [NOIP2023] 天天爱打卡
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P9871
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// Start coding at 2024-01-22 19:21:55
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL xds[1600001],lazy[1600001];
int ll[400001],rr[400001],v[400001];
int apos[400001],acnt;
vector<pair<int,int> > R[800001];
int n,m,k,d,qcnt;
LL dp[400001];
inline void input(){
acnt=0;
qcnt=0;
cin>>n>>m>>k>>d;
for(int i=1;i<=m;i++){
cin>>rr[i]>>ll[i]>>v[i];
ll[i]=rr[i]-ll[i]+1;
apos[++acnt]=ll[i];
apos[++acnt]=rr[i];
}
return;
}
void bulid(const int &now,const int &l,const int &r){
xds[now]=lazy[now]=0;
if(l==r)return;
int mid=(l+r)/2;
bulid(now<<1,l,mid);
bulid(now<<1|1,mid+1,r);
return;
}
inline void pushdown(const int &now,const int &l,const int &r){
if(lazy[now]){
lazy[now<<1]+=lazy[now];
lazy[now<<1|1]+=lazy[now];
xds[now<<1]+=lazy[now];
xds[now<<1|1]+=lazy[now];
lazy[now]=0;
}
return;
}
inline void pushup(const int &now){
xds[now]=max(xds[now<<1],xds[now<<1|1]);
return;
}
void mdf(const int &now,const int &l,const int &r,const int &sl,const int &sr,const LL &v){
if(l==sl&&r==sr)return xds[now]+=v,lazy[now]+=v,void();
pushdown(now,l,r);
int mid=(l+r)/2;
if(sl<=mid)mdf(now<<1,l,mid,sl,min(sr,mid),v);
if(sr>mid)mdf(now<<1|1,mid+1,r,max(sl,mid+1),sr,v);
pushup(now);
return;
}
LL qmax(const int &now,const int &l,const int &r,const int &sl,const int &sr){
if(l==sl&&r==sr)return xds[now];
pushdown(now,l,r);
int mid=(l+r)/2;
LL res=-1e18;
if(sl<=mid)res=max(res,qmax(now<<1,l,mid,sl,min(sr,mid)));
if(sr>mid)res=max(res,qmax(now<<1|1,mid+1,r,max(sl,mid+1),sr));
pushup(now);
return res;
}
int T;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>T>>T;
while(T--){
input();
sort(apos+1,apos+acnt+1);
int atot=unique(apos+1,apos+acnt+1)-apos-1;
// int L=1;
// for(int i=1;i<=atot;i++){
// if(L!=apos[i]){
// Ql[++qcnt]=L;
// Qr[qcnt]=apos[i]-1;
// }
// Ql[++qcnt]=apos[i];
// Qr[qcnt]=apos[i];
// L=apos[i]+1;
// }
// n=L;
for(int i=1;i<=m;i++){
ll[i]=lower_bound(apos+1,apos+atot+1,ll[i])-apos;
rr[i]=lower_bound(apos+1,apos+atot+1,rr[i])-apos;
R[rr[i]].push_back(make_pair(rr[i]-ll[i]+1,v[i]));
}
LL dp_0=0;
bulid(1,1,atot);
// cerr<<qcnt<<"\n";
for(int i=1;i<=atot;i++){
int K=i-(lower_bound(apos+1,apos+atot+1,apos[i]-k+1)-apos);
// cerr<<apos[i]<<"\n";
// cerr<<i<<" "<<dp_0<<" "<<K<<"\n";
int st=atot-i+1,ed=min(st+K,atot);//,lsted=min(st+1+Kl[i-1],atot);
// cerr<<st<<" "<<ed<<"\n";
mdf(1,1,atot,st,st,dp_0-d);
if(st!=ed)mdf(1,1,atot,st+1,atot,-d*(apos[i]-apos[i-1]));
// cerr<<i<<" "<<dp_0<<" "<<K<<"\n";
// cerr<<"end of normal modify\n";
for(auto pv:R[i])mdf(1,1,atot,st+pv.first-1,ed,pv.second);
R[i].clear();
dp[i]=max(dp[i-1],qmax(1,1,atot,st,atot));
if(apos[i]==apos[i+1]-1)dp_0=max(dp_0,dp[i-1]);
else dp_0=max(dp_0,dp[i]);
}
cout<<dp_0<<"\n";
}
return 0;
}
决策单调性
决策单调性就是指一个最优化 DP 的最优决策点是单调递增或单调递减的。
通常使用四边形不等式证明决策单调性。
四边形不等式
定义 ∀ l1≤l2≤r1≤r2,则四边形不等式即为 w(l1,r1)+w(l2,r2)≤w(l1,r2)+w(l2,r1)。简记为 交叉小于包含。
特别的,如果在等号时成立,那么该式子叫做四边形恒等式。
如果我们能证得 w(l−1,r)+w(l,r+1)≤w(l,r)+w(l−1,r+1),那么可以归纳证明这个关系满足四边形不等式。
并且我们定义 ∀ l≤l′≤r′≤r,如果有 w(l′,r′)≤w(l,r),则称该函数满足区间包含单调性。
由于四边形不等式是证明决策单调性的较为重要的方法,这里给出几个性质助于证明其满足四边形不等式。
性质 1
如果 w1(l,r) 和 w2(l,r) 均满足四边形不等式或区间包含单调性,那么对于任意 c1,c2≥0,均满足 c1w1+c2w2 满足四边形不等式或区间单调包含性。
证明显然,把拼凑出来的函数的式子拆开就能发现依然满足。
性质 2
若函数满足 w(l,r)=f(r)−g(l),则 w 函数满足四边形恒等式;当 f,g 函数还均满足单调递增时,那么 w 函数还满足区间包含单调性。
证明仍然可以把上面的式子拆成 f,g 做。
性质 3
若函数 h(x) 是一个单调递增的凸函数,且函数 w(l,r) 满足四边形不等式和区间包含单调性,那么复合函数 h(w(l,r)) 也满足四边形不等式和区间包含单调性。
性质 3,4 不知道怎么证,硬记吧。
性质 4
若函数 h(x) 是一个凸函数,且函数 w(l,r) 满足四边形不等式和区间包含单调性,那么复合函数 h(w(l,r)) 满足四边形不等式。
2D/1D DP 的优化
我们做区间 DP 时基本都会列出这样的式子:
引理:若 w(l,r) 满足区间包含单调性和四边形不等式,那么 fl,r 满足四边形不等式。
此时有定理:设 gl,r 为计算 fl,r 时的决策点,若 w(l,r) 满足区间包含单调性和四边形不等式,那么一定有:
此时做这种 DP 时,我们可以枚举 [gl,r−1,gl+1,r] 这个区间来枚举决策点。
这样可以使转移时对决策点的总枚举量做到 O(n2)。
例题
P1880 [NOI1995] 石子合并
这个东西之前我们的做法是 O(n3) 的,而可以通过四边形不等式决策单调性优化到 O(n2)。
首先,对于最小值,我们完全可以套上面的式子。此时 w(l,r)=prer−prel−1,肯定满足区间包含单调性和四边形不等式,那么可以使用决策单调性优化。
而最大值时,可以证明此时不满足决策单调性,但是此时一定会从最左极端和最右极端两个状态转移过来。因为最大时我们要尽量让大的状态尽可能的多被加。
总时间复杂度 O(n2)。
// Problem: P1880 [NOI1995] 石子合并
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1880
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-23 19:59:54
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
int a[10001],pre[10001];
int dpma[201][201],dpmi[201][201];
int g[201][201],n;
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i],a[i+n]=a[i];
n*=2;
for(int i=1;i<=n;i++)pre[i]=a[i]+pre[i-1];
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dpmi[i][j]=1e9;
dpma[i][j]=-1e9;
}
}
for(int i=1;i<=n;i++){
g[i][i]=i;
dpmi[i][i]=0;
dpma[i][i]=0;
}
for(int len=2;len<=n/2;len++){
for(int l=1;l<=n-len+1;l++){
int r=l+len-1;
dpma[l][r]=max(dpma[l][r-1],dpma[l+1][r])+pre[r]-pre[l-1];
for(int k=g[l][r-1];k<=g[l+1][r];k++){
if(dpmi[l][r]>dpmi[l][k]+dpmi[k+1][r]){
dpmi[l][r]=dpmi[l][k]+dpmi[k+1][r];
g[l][r]=k;
}
}
dpmi[l][r]+=pre[r]-pre[l-1];
}
}
int minn=1e9,maxx=-1e9;
for(int i=1;i<=n/2;i++){
minn=min(minn,dpmi[i][i+n/2-1]);
maxx=max(maxx,dpma[i][i+n/2-1]);
}
cout<<minn<<"\n"<<maxx;
return 0;
}
为什么复杂度是 O(n2):你可以理解为对于每一个 len,决策点 k 都只是从 1 遍历到了 n×2,所以是 O(n2) 的。
HDU3480 Division
首先对集合排序。
定义 fi,j 为前 i 个数分成 j 个集合的最小代价,有:
其中 w(l,r)=(ar−al)2。拆开式子其实可以发现可以斜率优化,但是决策单调性优化也是可以的。
显然 w(l,r) 满足四边形不等式与区间包含单调性。
而对于 fi,j=mink≤j(fi−1,k+w(k+1,j)) 这种转移式,它其实是一种分层的 1D/1D DP。
此时同样满足上面的引理和定理。而这道题的 w(l,r) 显然满足所有条件,所以有 gi−1,j≤gi,j≤gi,j+1,需要倒着枚举状态。可以优化到 O(nm)。
转移时尽量用下面的式子,转移更加方便。
// Problem: Division
// Contest: HDOJ
// URL: https://acm.hdu.edu.cn/showproblem.php?pid=3480
// Memory Limit: 999 MB
// Time Limit: 10000 ms
// Start coding at 2024-01-23 21:24:52
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
//#define int long long
int dp[10005][5005],g[10005][5005];
int a[10001];
int n,m;
int T;
int geta(int l,int r){
return (a[r]-a[l])*(a[r]-a[l]);
}
signed main(){
ios::sync_with_stdio(0);
cin>>T;
int ci=0;
while(T--){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
sort(a+1,a+n+1);
for(int i=1;i<=n;i++){
dp[i][1]=geta(1,i);
g[i][1]=1;
}
for(int j=2;j<=m;j++){
dp[n+1][j]=0;
g[n+1][j]=n;
for(int i=n;i>=j;i--){
dp[i][j]=1e18;
for(int p=g[i][j-1];p<=g[i+1][j];p++){
if(dp[i][j]>dp[p][j-1]+geta(p+1,i)){
dp[i][j]=dp[p][j-1]+geta(p+1,i);
g[i][j]=p;
}
}
}
}
cout<<"Case "<<++ci<<": "<<dp[n][m]<<"\n";
}
return 0;
}
P4767 [IOI2000] 邮局
定义 dpi,j 为 前 j 个村庄中设 i 个邮局的最小代价,列出 DP 方程式:
其中 w(l,r) 表示在 [l,r] 区间内设立一个邮局所需要的最小代价,显然取中位数最优。
发现和上面可以决策单调性优化的式子一模一样。尝试证明 w 函数满足四边形不等式。
首先尝试解决 O(1) 计算 w 函数的问题。画个图来理解一下:
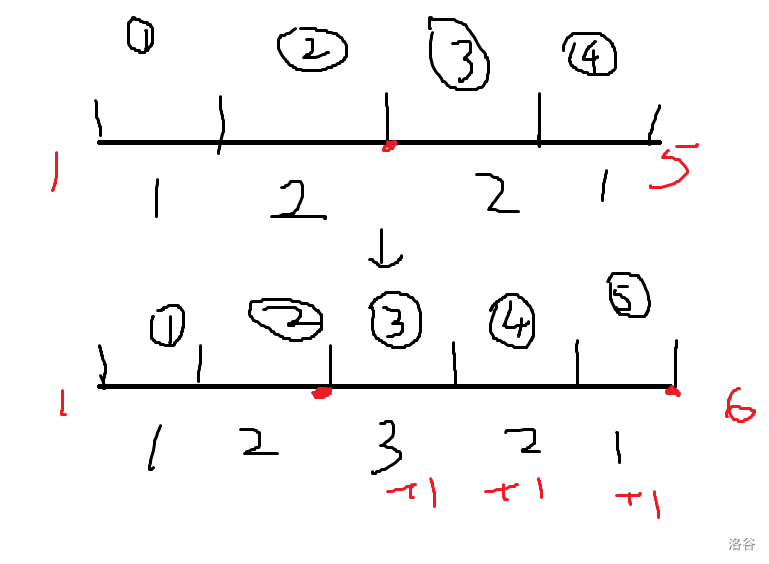
手玩发现从 w(l,r) 到 w(l,r+1) 只是把 [⌊l+r2⌋,r+1] 区间内点都经过了一遍,所以有式子:
接下来证明 w(l,r) 满足四边形不等式。
使用归纳证明:证明 w(l,r+1)+w(l−1,r)≤w(l−1,r+1)+w(l,r)。
拆开式子抵消可有:a⌊l+r2⌋≤a⌊l+r+12⌋,显然可证。那么有决策单调性:gi−1,j≤gi,j≤gi,j+1,倒序 DP 即可。
时间复杂度 O(PV+V2)。
// Problem: P4767 [IOI2000] 邮局
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4767
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-24 17:07:01
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
int w[3001][3001],V,P,a[3001];
int dp[305][3005],g[305][3005];
int main(){
ios::sync_with_stdio(0);
cin>>V>>P;
for(int i=1;i<=V;i++)cin>>a[i];
for(int l=1;l<=V;l++)
for(int r=l;r<=V;r++)
w[l][r]=w[l][r-1]+a[r]-a[(l+r)/2];
for(int i=1;i<=V;i++)dp[0][i]=1e9;
for(int i=1;i<=P;i++){
g[i][V+1]=V;
// for(int j=0;j<=V;j++)dp[i][j]=1e9;
for(int j=V;j>=i;j--){
dp[i][j]=1e9;
for(int k=g[i-1][j];k<=g[i][j+1];k++){
if(dp[i][j]>dp[i-1][k]+w[k+1][j]){
dp[i][j]=dp[i-1][k]+w[k+1][j];
g[i][j]=k;
}
}
}
}
cout<<dp[P][V];
return 0;
}
1D/1D DP 的优化
作者终于回来学 DP 了。
形如:
的 DP 方程式,同样与决策单调性有关。
有定理:如果 w(l,r) 满足四边形不等式,记 gi 为 f 函数在 i 处的最小最优决策点,那么有
在解决该问题之前,我们首先来解决其的弱化版:
形如:
的式子。同样满足上面的定理。
发现该转移根据 最优 一说,每次要枚举 gi−1∼i−1 这个区间,时间复杂度仍是 O(n2) 的。
所以我们想办法求出上界。
因为这个 g 数组一定是一个不降的数组,所以我们考虑对 g 数组分治求。考虑首先算出 gmid,然后对于左右区间就有一个上界或下界了。
例题 1:LOJ 6039「雅礼集训 2017 Day5」珠宝 /「NAIPC2016」Jewel Thief
这是一个分层 DP,所以列出来的 DP 式子让人以为这个 DP 是上面的非弱化版,而实际上,这个 DP 是刷表,于是如果这个 DP 满足决策单调性,那么就可以直接分治。
首先把 DP 式子列出来。
首先注意到此题 c≤100,而 n 远大于 c,于是我们设 dpi,j 是选过前 i 种价值,背包已有容量为 j 时的最大价值。有:
其中 w(i,k) 指在容量为 i 时选 k 个的最大价值,也就是从大往小选。
此时考虑将 j−ki 和 j 放到一个同余系下转移,即 modi 同余系下,有:
其中 w′i(k,j)=w(i,k−ji)。显然满足四边形不等式。
把 i 滚掉,我们就把方程式化成了:
而这是一个刷表,所以在计算时,我们是知道了上一维的 dp 数组的,也就是说,这里的每一个 dp 数组都是可以直接算出来而不需要之前当前维的 dp 方程组,所以可以直接分治。时间复杂度 O(cklogk)。而对于 max 类问题,我们可以直接将所有数取反就能得到关于 min 的式子,两者其实是一样的。
注意这个式子满足决策单调性的前提是在同余系下,所以对于不同同余系我们分开分治。具体就是将一个同余系里的所有元素提出来分治,最后再赋值回去。
例题 2:P3515 [POI2011] Lightning Conductor
纯纯拆式子题。
对式子进行变形,得到:
由于 p 尽量小,于是我们知道:
将绝对值拆开,并提出中间的 j 无关项,得到:
我们可以倒置整个数列并使用相同的方法来维护 j>i 的情况,于是下面我们只讨论 j<i 的情况。
注意到之前我们列出的弱化版式子
满足决策单调性优化条件并且可以直接分治,于是我们考虑将上面计算 p 的式子向这个式子靠拢。
首先是 max 转 min:
然后就是证明 w(j,i)=−aj−√i−j 满足四边形不等式了,这个是容易的,根据
得到 f(n)=√n 的增长速度渐缓。
根据归纳证明,我们可以得到:
结合 增长速度渐缓,显然 w 满足四边形不等式。
那么可以直接分治两次,注意取整方向。
神秘的是,这道题必须开 long double 才能行。
练习完弱化版以后,我们回到原问题上。
考虑对于一个式子 fi=minj<i(fj+w(j,i)),我们不一定到了 i 才去比较哪个最优,换一种思路。我们假定有一种方法使我们到了 i 就已经知道这里的最优决策点了,那么我们就要考虑每次加入一个点去更新后面部分的最优决策点。广义李超线段树是可以的,这里暂不提及。
我们发现对于两个决策点 i,j 来讲,如果描述这两个策略的函数只有一个交点的话,我们能二分出一个点,使得对于只有 i,j 两个决策点时,其左侧与右侧选的策略不一样。于是我们可以利用这个性质来处理上面式子的转移。
维护一个单调队列,元素为 l,r,p,即第 p 个位置的决策区间是 [l,r],其内元素从队首开始都能被后面的一个元素在 ki 处被取代,且 ki 升序。加入一个点就分两种操作:
- 踢出已经过时的决策:当队首的决策区间右端点小于目前正在枚举的下标,弹出队首。
- 加入新的策略:当目前最新的一个策略能在一定时候超越队尾,就加入。如果目前最新的策略超越队尾的时间比队尾超越上一个策略更靠前,那么就弹出队尾。
每次取队首就是最优决策点。
上述方法简称二分队列,时间复杂度为 O(nlogn)。
例题
P1912 [NOI2009] 诗人小G
首先列出 DP 方程式,设 fi 是前 i 个的最小不协调度。有
其中 s 数组代表所有句子末尾带空格后的前缀和。令 w(j,i)=|si−sj−1−L|P,接下来我们证明 w 满足四边形不等式。
同样,我们归纳证明。有
根据题意,s 数组严格升序,不难发现左右两式都是在不同的位置取间隔长为 sl−sl−1 的两条竖线与函数 f(x)=xP 的交点右减左的纵坐标差,显然右式更加远离负无穷处。
根据 f(x)=xP 的导数,在 P≥2 时导数严格上升,在对称轴左侧函数值为负,故跨越对称轴的区间从左到右的右减左函数差严格递增,且根据趋势,上式满足。
在 P=0,1 时左右两式相等,同样满足。
故 w 函数满足四边形不等式。
那么满足直接二分队列。
另类优化
同样是 1D/1D,但是这个并不能算是决策单调性优化,因为这个满足不了决策单调性的定义。
使用这个方法的前提是,有两个决策 i,j 满足 i<j 且原本 j 的函数值较优,后面经过分界点 k 后变为 i 比 j 优。且两个决策的函数图像只有一个交点。
不难发现越往后的决策最后会被前面的决策超越,所以我们想到用单调栈维护,维护的信息和上面的二分队列一样。
我们同样分几种情况讨论:
- 直接扔掉:如果当前策略已经比在栈中的策略劣,直接跳过。这个适用于二分完之后发现栈顶的策略就在正在枚举的这里超过的目前的策略。
- 弹出:如果栈顶的决策区间 r 小于目前所遍历到的下标,弹出栈顶。
- 加入:二分超越时间,如果栈顶被栈次顶超越的时间比栈顶超越新决策的时间早(或相等),那么弹出栈顶,一直操作直到符合条件。
同样的,我们称这种方法为二分栈。时间复杂度同样为 O(nlogn)。
例题:P5504 [JSOI2011] 柠檬
首先框定贡献来源,如果选的区间 [i,j] 中 si≠sj,如果选 sj,那么一定去掉 i 更优;如果选 si,那么一定去掉 j 更优,如果既不选 si,又不选 sj,那么都去掉最优。所以最优选取区间有性质:si=sj。那么令 prei 是前 i 个贝壳中有多少个大小为 si,可以列出方程式:
后半部分并不满足决策单调性,而且对于转移我们要分颜色转移,所以不能使用二分队列。由于对于每种颜色,prei−prej 的 j 越靠左其值越大,结合其图像不难发现越靠左侧的策略最终会超越靠右侧的策略。那么适用于二分栈。
但是特殊的是,由于我们只能同颜色转移,所以我们要开颜色个数个栈来进行转移。
注意最后推入栈时的决策区间左右端点与推入队列时有一点小小的区别。
二分队列,二分栈是只要决策满足特殊性质且满足函数间只有一个交点且函数易求其值就可以用的。之后可能拿之前用分治做过的题来练习二分队列和二分栈。
对于分治的优化
上面的 1D/1D DP 我们提到了一种分治的方法来优化 DP,但是如果在分治过程中贡献较为难算该怎么办?回忆我们当初写整体二分的思路,我们用类似于莫队的双指针法来维护其区间不同颜色个数,由于每次二分左右区间相同,所以指针移动幅度和区间大小一致,复杂度不变,仍然为 O(nlogn)。
例题
斜率优化会专门开一个版块,先练习练习上面的 DP 优化方式。
CF833B The Bakery
列出方程式,即设 fi,j 为前 i 个正好分 k 块的最大价值。
对于每一层 ki,同层之间没有转移,且 w(l,r) 为 [l,r] 区间内的颜色个数,让人想到决策单调性 DP。2D/1D 的那种方法不能做因为那种方法是条件苛刻,并且这道题贡献难算,而不难发现 w 恰好反向满足四边形不等式。
于是想到 max 转 min,方程式变为 fi,j=mink<j(fi−1,k−1−w(k,j)),−w 函数满足四边形不等式,于是该方程式具有决策单调性,从而具有分层分治的条件。−w 函数的求解使用双指针优化,时间复杂度 O(nklogn)。
P5574 [CmdOI2019] 任务分配问题
我居然不会区间逆序对的 O(n√mlogn) 的莫队+树状数组做法了,直接震惊我了,DS 也急需补了/kk
考虑题意让我们把一个序列分成 k 段,使得 k 段中的顺序对和最小。一样的思路,使用优化分治法,用树状数组来做双指针顺序对,现在就只剩排列的区间顺序对的个数满足四边形不等式的证明了。
归纳证明,考虑最极端的时候,w(l−1,r) 正好是 w(l,r)+r−l+1,w(l,r+1) 正好是 w(l,r)+r−l+1,这时 w(l−1,r+1) 就是 w(l+r)+r−l+1+r−l+2,仍然大于。剩余的情况就几乎一样了。
至于如何用双指针+树状数组来求区间顺序对。开值域树状数组,左侧删就是减去大于该数的个数,就是区间长减去小于等于这个数的个数,并将这一点在值域树状数组上删掉(该位置 1→0),左侧加就是加上大于该数的个数,在树状数组上加上该数(该位置 0→1),右侧基本一致。
时间复杂度 O(nklog2n),有点卡。
事实证明,lowbit 不写函数会显著提升效率。
CF868F Yet Another Minimization Problem
一样的套路,再来一遍。
这次换成了相同元素对个数,这下四边形不等式证明显然了,就是 w(l−1,r+1) 一定包含 l−1 对 [l,r] 的贡献和 r+1 对 [l,r] 的贡献,而甚至 l−1 还可能对 r+1 有贡献,所以铁打的满足四边形不等式。
莫队求相同元素对甚至有模板题,开一个桶就结束了,时间复杂度 O(nklogn)。
就是以后别忘了分层决策单调性和之前提到的弱化版式子有分治做法优化复杂度,别忘了贡献难算时直接上类莫队的双指针就行了。
P4072 [SDOI2016] 征途
拆方差的式子,设总路长为 t,可得:
所以我们知道 w(l,r)=m×(prer−prel)2,有方程式:
其中 fi,j 表示前 j 个里分 i 段,实际代码中我们是设的 fi,j 是前 i 个里分 j 段,这里有点差别。
拆式子即可证得 w(l,r) 满足四边形不等式,那么可以使用决策单调性分治或者特殊分层 DP 决策单调性优化(gi−1,j≤gi,j≤gi,j+1)来求解。
决策单调性分治:AC 记录,时间复杂度为 O(nmlogn)。
分层决策单调性优化:AC 记录,时间复杂度为 O(nm+n2)。
为什么后者跑不过前者呢?小编也不知道,而且后者由于要开两个二维数组,差点爆空间/ch,所以要谨慎选用方法(其实可以用滚动数组)。
CF321E Ciel and Gondolas
同样的方程式,不过 w(l,r) 变成了矩阵中 (l,l) 和 (r,r) 组成的子矩阵的元素和的一半。这个东西用二维前缀和可以做到 O(1) 求。稍微框定一下矩阵你就知道这个东西满足四边形不等式了。
同样的有两种方法求解。
决策单调性分治:AC 记录,时间复杂度为 O(nklogn),较为卡,但是加上快读据 gyy 说就直接快 1.3s 起飞!
分层决策单调性优化:AC 记录,时间复杂度为 O(nk+n2),但是为什么只快了 100ms 捏?也许这个方法的常数有点大吧。
P4360 [CEOI2004] 锯木厂选址
原来听 zhicheng 说这题是斜率优化所以没做,今天发现决策单调性秒了。
首先对于第一个和最后一个锯木厂直接暴力转移,中间的锯木厂进行 DP。
设第一个锯木厂建在 i 处对于前 i 个的花费是 gi,有:
一眼就是决策单调性的形式。
w 函数是把 [l,r] 之间的木材全部运到 r 处的花费,发现不太好算,于是想到优化型分治做法。证明 w 函数满足四边形不等式也是容易的,随便画一下图就能发现 w(l−1,r+1) 对于 w(l,r) 的额外贡献大于 w(l−1,r) 和 w(l,r+1) 对于 w(l,r) 的额外贡献之和。
那么直接分治即可,时间复杂度 O(nlogn)。
到这里,决策单调性的题就暂告一段落了。
下面我们来讲一讲一个使用范围更广的优化方法:斜率优化。
斜率优化
斜率优化主要针对于转移可以写成一次函数的 DP,其通常形式为:
其中 pi,pj 分别是只关于 i,j 的一些项,C,t 是常数。
我们可以把后面这一部分写成 minj<i(tji+pj+fj)+pi+C 的形式,令 k=tj,b=pj+fj,那么我们就把这个转移写成了一个一次函数加上一些只关于 i 有关的项。如果我们能保证对于关于 j 往后的每一个转移 j→i,t 和 pj 是完全一致的,我们就可以使用斜率优化。
这样我们就可以使用一些性质来维护这堆一次函数。显然我们其实每次转移就变成了在横坐标轴上砍一刀,取当前函数值最大或最小的一个一次函数作为转移。那么其实就是维护一个上/下凸壳。
一般我们有两种该视角下的常见斜率优化方式。
首先是条件最苛刻的,即优化我们的二分队列/二分栈,要求是满足二分队列/二分栈的特殊性质,并且可以写成一次函数形式。具体和二分队列/二分栈一致,不过我们不需要二分了,可以直接求交点。时间复杂度直接降到 O(n)。翻译成斜率优化的术语就是如果顺序转移,并且斜率原来就有序,那么就可以使用单调队列/单调栈做。
第二种就是什么也不满足,直接上李超线段树,时间复杂度 O(nlog2n) 或 O(nlogn)。
但是我们讲斜率优化更常用的是另一个视角。考虑直接讨论一个策略比另外一个策略优秀的前置条件,如果它能够写成一个类似于 pi−pjci−cj<T 的形式,其中 T 仅与 i 有关,那么我们就可以把左式当做一个斜率来维护,那么我们就要维护一个凸壳。
第一种就是决策点单调并且每次插入的斜率单调,那么直接上单调队列就能 O(n) 解决。
第二种就是插入斜率单调,但是决策点不单调,这样的话我们只能每次通过上面那个式子在单调队列上二分找出最优决策点,时间复杂度 O(nlogn)。
第三种是插入斜率不单调,决策点单调,这个时候说是可以什么平衡树,但是如果复杂度没有太高要求可以直接用第一个视角的方法李超线段树性价比最高。
第四种是插入斜率与决策点均不单调,可以用平衡树/CDQ 分治做,但是作者目前没有太看懂,等遇到该类型的题时再作讨论。
首先先不急着做题,首先来学习一下斜率优化万能做法:李超线段树。
李超线段树
李超线段树是一种用于维护平面直角坐标系内线段关系的数据结构。
大概就是每次插入一条直线/线段,问与直线 x=k 相交的线段中交点纵坐标最大/小的线段的编号或纵坐标最大值。
我们主要维护区间内的一个最优线段,定义最优线段为区间中点纵坐标最大的一条线段。插入时,如果当前区间内目前没有最优线段,那么直接把这个线段作为最优线段。如果有,首先来判断目前谁是最优线段,如果原最优线段已经不是最优线段了,那么我们直接交换两者。并且将非最优线段的那个线段递归下传。
根据两个非重合的线段至多有一个交点,那么这个最优线段在某一部分可能是不优于另一个线段的,如果该线段左端点纵坐标比最优线段大,那么用该线段递归左区间,如果右端点大,那么递归右区间,如果都小,那么直接返回。
查询时对于一个点在递归途中的所有线段取 max,而不是直接取某一点的最大线段。因为李超线段树使用的是类似于标记永久化的方法,所以存的信息是层数越低越有时效性。
感性理解其就是正确的。
由于线段我们要把定义域拆分为 O(logV) 个区间,于是复杂度是 O(log2V),直线就直接是一个区间,时间复杂度 O(logV)。大多时候使用动态开点线段树。
模板题:P4097 [HEOI2013] Segment
如果遇到插入一个竖线,把其转化为插入一个定义域在 [x,x] 上的一次函数 y=0x+max(y0,y1) 即可。
板子代码:
// Problem: P4097 【模板】李超线段树 / [HEOI2013] Segment
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4097
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Start coding at 2024-02-20 15:58:36
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
int n;
int op,X1,Y1,X2,Y2,kk;
struct line{
long double k,b;
int xl,xr;
long double operator()(const int x){
if(xl<=x&&x<=xr)return k*x+b;
return -1e18;
}
void init(){
xl=X1,xr=X2;
if(xl==xr){
k=0;
b=max(Y1,Y2);
return;
}
k=1.0*(Y1-Y2)/(X1-X2);
b=0.0+Y1-k*X1;
return;
}
}f[100001];
int cnt;
struct LCT{
#define mid ((l+r)>>1)
int xds[400001],ls[400001],rs[400001],tot,rt;
void upd(int &now,int l,int r,int id){
// cout<<l<<" "<<r<<" "<<id<<" "<<xds[now]<<"\n";
if(!now)return now=++tot,xds[now]=id,void();
if(!xds[now])return xds[now]=id,void();
// cout<<"2 phase\n";
if(f[xds[now]](mid)<f[id](mid))swap(id,xds[now]);
if(f[id](l)>f[xds[now]](l))upd(ls[now],l,mid,id);
else if(f[id](r)>f[xds[now]](r))upd(rs[now],mid+1,r,id);
return;
}
void ins(int &now,int l,int r,int sl,int sr,int id){
// cout<<l<<" "<<r<<" "<<sl<<" "<<sr<<" "<<id<<"\n";
if(!now)now=++tot;
if(l==sl&&r==sr)return upd(now,l,r,id),void();
if(sl<=mid)ins(ls[now],l,mid,sl,min(sr,mid),id);
if(sr>mid)ins(rs[now],mid+1,r,max(sl,mid+1),sr,id);
return;
}
int qu(int now,int l,int r,int x){
// cout<<l<<" "<<r<<" "<<x<<" "<<xds[now]<<"\n";
if(!now)return 0;
if(l==r)return xds[now];
int rid;
if(x<=mid)rid=qu(ls[now],l,mid,x);
else rid=qu(rs[now],mid+1,r,x);
if(fabs(f[xds[now]](x)-f[rid](x))<1e-7)rid=min(rid,xds[now]);
else if(f[xds[now]](x)>f[rid](x))rid=xds[now];
// cout<<l<<" "<<r<<" "<<x<<" "<<rid<<" backing\n";
return rid;
}
#undef mid
}t;
int lst;
int main(){
ios::sync_with_stdio(0);
cin>>n;
f[0].xl=1;
while(n--){
cin>>op;
if(op){
cin>>X1>>Y1>>X2>>Y2;
X1=(X1+lst-1)%39989+1;
X2=(X2+lst-1)%39989+1;
Y1=(Y1+lst-1)%1000000000+1;
Y2=(Y2+lst-1)%1000000000+1;
if(X1>X2)swap(X1,X2),swap(Y1,Y2);
f[++cnt].init();
// cout<<f[cnt].k<<" "<<f[cnt].b<<"\n";
t.ins(t.rt,0,39989,X1,X2,cnt);
}else{
cin>>kk;
kk=(kk+lst-1)%39989+1;
lst=t.qu(t.rt,0,39989,kk);
cout<<lst<<"\n";
}
}
return 0;
}
实现的较为复杂。
练习题:P4254(直线)。
李超线段树有时值域过大需要离散化,这个时候实际上是整一个序列包含所有的坐标然后依靠序列的值建李超线段树。如果保证两线没有交点那么可以做到 O(logn) 线段插入,即没有下传标记。并且李超线段树其实支持求某一个横坐标下第一个函数值小于某一个值的线段的编号。
上面说的东西糅合在一起就是 P3081。
方法都讲完了,下面直接开始练习。
例题
练习题:P3195,P5785,P3628,CF311B,P4655,P5017,P2900。
P3195 [HNOI2008] 玩具装箱
这个题非常典。首先要设 Pi=prei+i,此处的 L 比原题的 L 大 1。
列出 DP 方程式:
拆开后面的式子:
只关于 i 和 L 的项直接拿出来,剩下的项就有:
这坨东西可以拆成:
这个东西显然可以直接用一条只与 j 有关的直线表示,其中 k=−2Pj,b=fj+P2j+2PjL,x=Pi。显然发现 k 单调递减,x 单调递增且求最小,那么可以使用单调队列维护。时间复杂度 O(n)。
P5785 [SDOI2012] 任务安排
这个题有 O(n2) 的弱化版,详见 Problem_unruled_record。
拆方程式:
后面那坨是一个 kx+b 的形式,可以使用斜率优化。因为 preti 不单调,所以使用李超线段树。
时间复杂度 O(nlogV),离散化后为 O(nlogn)。注意不离散化时候的李超线段树会出现询问横坐标为负的最小值,所以李超线段树的值域为 [−V,V],V 为可能询问到的最大的数,大约是 109 级别。
其实有这两道题的讲述就够了,剩余题看上面 AC 链接的代码就行了。
说白了就是要大胆拆式子。
CF311B Cats Transport
自认为极好的一道题,反映出我一堆问题。
于是这道题我会单独拿出来写。
P5017 [NOIP2018 普及组] 摆渡车
什么 DP 方程式之类的容易,不过注意摆渡车不一定在正好有人等车时间为 0 的时候出发,之前那几道题都是因为这样做一定优,而这道题不是。
然后就直接暴力对时间维斜率优化,时间复杂度 O(t),如果对有用状态做斜率优化能做到 O(nm+nlogn)(包含离散化)。
P2900 [USACO08MAR] Land Acquisition G
写这道题主要是写它的转化。
注意到如果存在 i,j 满足 wi≥wj,hi≥hj,那么如果在买 i 土地时顺带把 j 土地买了就不会增加代价。所以我们把含有被包含关系的土地删掉,具体就是对于首先按照 h 排序(w 为第二关键字),然后维护 w 的后缀最大值,如果存在一个点 i,使得 sufmaxi+1≥wi,那么第 i 个土地一定被包含。
然后就是会发现做完上面的操作之后,剩下的序列满足 h 递增,w 递减。发现如果买第 l,r(l≤r) 个物品时所花的代价为 wlhr,并且这个长方形包含了 [l,r] 的所有土地,可以一并购买。所以原问题就转化为了在该序列上进行分段问题,求所有段代价和最小,那么显然有 DP 方程式:
显然的斜率优化形式,其中 k=wj,b=dpj−1,x=hi,显然满足 k 递减,x 递增,那么直接上斜率优化即可。
时间复杂度 O(nlogn+n),瓶颈在排序。
分治
这个东西主要是 CDQ 分治,千变万化。然而我已经忘完了。
类型一:删去一个点后的贡献(互相独立)
直接 CDQ 分治,需要满足 DP 顺序可以被任意打乱并且 DP 数组较小。每次暴力加入 [l,mid] 的物品并递归 (mid,r],然后暴力加入 (mid,r] 并递归 [l,mid]。递归到 l=r 时就不加入直接处理删去该点的询问。
推荐记录每一层的 DP 数组,这样可以在赋初值或撤销时可以直接从上一层转移下来,减小常数。
例题:P4095 [HEOI2013] Eden 的新背包问题
多重背包。显然物品可以打乱加入。这里需要单调队列优化多重背包,时间复杂度 O(nVlogn)。
类型二:跨越 mid 的转移(非偏序题)
具体就是在一个非偏序题中,先递归左侧,然后将 [l,mid] 转移到 (mid,r],再递归右侧。
通常,这样的转移复杂度是假的,但是在某些题中可以先遍历 [l,mid],然后记录一些信息做到可以通过这些信息直接转移到 (mid,r],并且复杂度在 O(1) 或 O(logn) 级别。感觉只有在二维问题中会用到这样的优化,因为理论上这个优化完完全全可以被其他更优秀的优化方式平替。
例题:P3120 [USACO15FEB] Cow Hopscotch G
考虑对 W 一维分治,每次把转移做成在 W 轴上的 [l,mid] 转移到 (mid,r],那么从下到上枚举 H 一维,维护前面枚举到的东西的和,并且维护每个颜色对应的和,然后再遍历 (mid,r],通过全部减去相同颜色的方案数来转移。
这里需要用到一个技巧,即维护当前每个颜色对应和的版本(其实不用,但是其他时候可能用到),每次转移时版本加一,然后如果记录的版本小于现在的版本,更新其版本并置 0。后面就正常统计即可。
类型三:偏序类问题
比较典的一类问题。和上面的东西基本一样。但是有很多潜在性质,比如时间顺序等。
例题:P4093 [HEOI2016/TJOI2016] 序列
假设我们对于一个点上的所有变化取一个最大和最小值,那么这个 DP 满足:
直接 CDQ 分治 + 树状数组解决,时间复杂度 O(nlog2n)。
类型四:数点
这个东西单点带修也能做。
具体就是类似于归并的操作,把询问与原来的值放进一个数组里,然后按某一维排序。首先向左向右递归,然后双指针扫一遍。因为此时左边的值对于某一维有序,右边的值对于某一维有序,并且此时左边的所有点都在先前排序的那一维满足条件,那么扫到左边的值时,答案加一;扫到右边的询问时,将当前答案赋到其对应的数组中。最后别忘了归并时需要一个辅助数组,注意保证其在每一层的大小均为 r−l+1。
最板子的题:P2163 [SHOI2007] 园丁的烦恼
可以离线树状数组,记录见 Problem_unruled_record。
当然也可以 CDQ。把原来的值和询问全部放到一个数组里,然后按 x 排序,再对 y 归并时统计答案。时间复杂度 O(nlogn)。
带修:P4390 [BalkanOI2007] Mokia 摩基亚
强行加一维时间维,需要满足 x′≤x∧y′≤y∧t′≤t 才满足条件。同样对 x 排序,对 y 归并(其实此处直接 sort 复杂度不变),树状数组统计小于 t 的所有贡献,时间复杂度 O(nlog2n)。
作者去颓了,明天下午继续。
WQS 二分
等考到再学。(人话:下个赛季再说)
矩阵加速
朴素
经典的矩阵加速题在上面已经提及,下面有几个特殊的例子:
例题:P2579 [ZJOI2005] 沼泽鳄鱼
首先建出图的邻接矩阵,对于每种可能的食人鱼的情况(最多 12 种)每次将食人鱼所在的一列全部删完。
然后以 12 为周期进行矩阵快速幂。
例题:P3216 [HNOI2011] 数学作业
设答案向量为 [ans,nxt,1],nxt 为下一个要加的数,1 为加的数的增量。那么转移矩阵显然是:
按每个数的位数分段进行矩阵快速幂即可。代码中开了 __int128。
__int128 不能用数学库里的函数。
广义矩阵乘法
这个时候的快速幂就没有什么单位矩阵了,需要认真展开写,而不是整一个什么单位矩阵左乘。
假设有:
如果满足:
- ⊕ 满足交换律。
- ⊗ 满足交换律和结合律。
- (a⊕b)⊗c=(a⊗c)⊕(b⊗c)。
那么该运算满足广义矩阵乘法结合律,可以使用矩阵快速幂。称该乘法是 (⊕,⊗)。
常用:(max,±),(min,±),(or,and)。
例题:P2886 [USACO07NOV] Cow Relays G
考虑类 floyd。显然是 (min,+) 乘法,可以使用快速幂。需要离散化,初始矩阵为邻接矩阵。
例题:P3502 [POI2010] CHO-Hamsters
考虑 n≤200,所以我们可以暴力哈希 O(n|Σ|) 预处理出最长的公共前后缀。
然后考虑一个类似 floyd 的东西,就是答案矩阵显然左乘上转移矩阵就是 m→m+1 的转移,同样显然是 (min,+) 矩阵乘法,转移矩阵的 i,j 是当前末尾为第 i 个串,下一个要到第 j 个串还需要添加的字符数,根据互不包含的性质发现正确。快速幂即可。
这东西还有双倍经验,那题解就不得不写了(偷笑)。
详细题解:
考虑暴力 DP,设 dpp,i,j 为目前已经出现过 p 次,最开始的字符串为第 i 个串,末尾的字符串为第 j 个串,所要使用的最短字符个数。
那么设 gi,j 为末尾为第 i 个串,后面想再出现一次第 j 个串最少需要添加多少字符。这个东西有点像一个 KMP,但是可以直接哈希暴力从大到小枚举 gi,j,时间复杂度为 O(n|Σ|),可以接受。
预处理 g 之后,我们注意到题中给出的是 n 个互不包含的串,所以有:
显然是广义矩阵快速幂优化的形式,把 p 一维滚掉,考虑 (min,+) 是否满足广义矩阵乘法的结合律。
众所周知,广义矩阵乘法 Ai,j=⨁nk=1(Bi,k⊗Ck,j) 满足结合律时满足以下条件:
- ⊕ 满足交换律。min(a,b)=min(b,a)。
- ⊗ 满足结合律与交换律。a+b+c=a+(b+c)=a+(c+b)。
- ⊗ 对 ⊕ 有分配律。min(a,b)+c=min(a+c,b+c)。
发现 (min,+) 以上三条限制均满足,那么可以使用矩阵快速幂优化,时间复杂度 O(n|Σ|+n3logm)。
代码写的很丑,不喜勿喷。
baka's trick
这是优化双指针的一种方式,感觉本质是双栈模拟队列。
有些时候双指针只能满足加元素与合并两个区间的答案,而无法删除元素时,就需要使用这个 trick。
考虑我们有两个栈 s1,s2,并设一个中间值 mid,s1 就存的是 [l,mid] 的所有答案,s2 存的是 (mid,r] 的所有答案。考虑初始设置 r=1,l=r+1,mid=r,对于当前任意一个 r=k,我们先将 l 左边的元素加入 s1,直到无法满足题中条件,计算 [l,r] 答案时则需合并 s1,s2 的答案。这个时候不难发现这是 r=k 时的最小 l,此时再把下一个 r 加入 s2 中。这时显然 l 只能撤销,撤销到 [l,r] 满足条件即可。如果出现 l>mid,即 s1 为空,那么显然需要重构双栈,即 mid=r,l=r+1。
在实现时没有必要显式的把两个栈建立出来,用两个数组代替也行。
例题:CF1548B Integers Have Friends
差分。这样能抵消掉余数的影响,原问题转化为求最长的区间 gcd 大于 1 的子段长。
按上面的方法回滚双指针即可。时间复杂度 O(nlogV)。记得开 long long。
例题:FLOJ2439 [2019 五校联考镇海 B] 小 ω 的仙人掌
小 ω 有 s 个物品,每个物品有一定的大小与权值。
她可以从任意第 L 个物品走到第 R 个物品,这个区间内的物品可以选或者不选。
她取出的物品大小和必须为 w ,权值和必须 ≤k。
她想知道这个区间最短是多少。
01 背包。众所周知,背包是非可删除的,所以需要用回滚双指针。之前的双指针都是求最长,这里是求最短,其实差不多。考虑左指针向左移的条件变为 当前情况不能满足,左指针右移的条件是 当前情况能满足,下一个情况也能满足 即可。
时间复杂度 O(sw)。
这边作者没时间写了,明日再战。DP 总算快要结束了。
一堆细节。注意清空与 l,r 指针的边界。
拓展
前面提到了 双栈模拟队列,可能大家觉得这个与 DP 的关系不是很大,但是恰恰相反,很多 DP 是用了栈的性质才能做到合理撤销的,所以学习栈模拟其他数据结构极其重要。
首先是双栈模拟队列,考虑开 2 个栈 s1 和 s2,加入元素通过 s1,删除元素通过 s2。
对于加入元素,直接加入 s1 即可。对于删除元素,如果 s2 为空,那么对 s1 进行弹出,然后加入到 s2 的操作,直到 s1 为空,然后弹出 s2 栈顶即可。
显然每个元素最多被弹出 2 次,最多被加入 2 次,均摊下来每次操作的时间复杂度为 O(1)。
画个图理解一下:
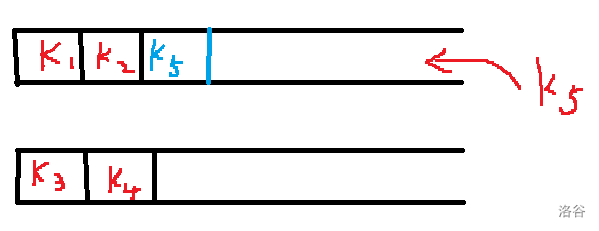

差不多就是这样,后面的双端队列也是这个思想,就不放图了。
接下来就是最难的地方:双栈模拟双端队列。
这个东西很有均摊的味道,大家都说的是 暴力重构,但是我习惯说是三栈模拟双端队列。
首先开 3 个栈:s1,s2,s3。s1 负责队首,s2 负责队尾,s3 是临时栈。
考虑加入的时候还是直接加入 s1,s2 中,在弹出的时候如果遇到该栈为空,那么就先把另外一个栈内的一半元素加入到 s3 中,再把另一半元素加入到正在弹出的栈中。此时这两部分元素均为逆序。再把 s3 内所有元素加入回另一个栈中,这部分就回归顺序。
考虑时间复杂度,每次我们把元素均匀分在了两侧,那么对于弹出操作,第一次弹出最多 O(n) 个元素,第二次弹出 O(n2) 个元素,有 O(n)+O(n2)+O(n4)+⋯=O(n),所以弹出的总复杂度是 O(n) 的,均摊下来单次复杂度就是 O(1) 的,不过常数可能有点大。
这就非常厉害了,如果要在双端队列上维护一些不可删除并且能较快合并的信息,比如 gcd,背包等,我们就可以合理撤销,做到 O(n(w+h)),其中 w 是插入一个元素的复杂度,h 是合并两个栈答案的复杂度。
这下大家应该能理解前面的 baka's trick 就是双栈模拟队列的一种形式了吧。
例题:LOJ6515 「雅礼集训 2018 Day10」贪玩蓝月
双栈模拟双端队列,然后就是 DP。设 dpi,j 为前 i 个物品特征值模 p 值为 j 时的最大战斗力。显然有最简单的转移:
对于 s1,s2,加入元素时 DP,弹出元素时撤销。然后我们只需要讨论如何合并两个栈的贡献。
显然这是一个类 (max,+) 卷积,暴力做是 O(p2) 的。但是我们没有必要显式的计算卷积后的每一个值,我们只需要计算区间 [l,r] 的最大值就行了。所以我们考虑对于 s1 的每一个 fi,满足条件的 gi 就只有 gl−i∼gr−i,所以可以复制 g 数组一次(类似断环为链),然后用单调队列扫一遍就能出答案,时间复杂度 O(p),总时间复杂度 O(mp)。
手写一个栈非常有意思。
稍微说下一个离线做法吧,作为之后学线段树分治的引子。
考虑建出线段树,在线段树上记录下每个物体的存活区间,打上永久化标记,然后 dfs 一遍这个线段树就行了,需要支持加入一个元素,撤销上一次加入。一共有 O(mlogm) 个标记,时间复杂度就是 O(mplogm),空间复杂度相对较优,为 O(plogm)。
这个做法就劣在无法使用上 双端队列 这个性质。
动态 DP
最史的一集。
首先,动态 DP(DDP)就是带修的 DP,通常需要使用数据结构优化算出答案的过程。简而言之,就是抽象成,有一堆元素,每次修改一个(区间内的)元素,询问经过某些操作后的结果。而 某些操作 就是 DP 的转移式子。
通常来讲使用矩阵维护。一半用来解决树上带有点权(边权)修改操作的 DP 问题。
动态 DP 题很稀少,并且需要用到广义矩阵乘法,因此并不常用。(而且很难调)
这一节会有一堆广义矩阵乘法的东西,需要一个一个分讨,较为复杂。(人话:不想写)
作者会尽量描述准确。
这东西只能用例题来描述。
动态最大权独立集
首先定义最大权独立集。对于 G=(V,E),有 V′⊆V 使得 ∀a,b∈V′,(a,b)∉E,并且 V′ 是满足条件的集合的点权和最大的一个,则 V′ 为该图上的最大权独立集。
考虑这个东西是 NP-Hard 的,所以这个问题一般规约到树上或者二分图上。这里只讨论树上带修的情况。
即:支持单点修改,查询全局最大权独立集的权值和。
首先我们设计最简单的 DP:设 fi,0/1 为点 i 的子树中 i 点选/不选的独立集的点权和最大值。显然有:
设一个点的矩阵为 [fi,0,fi,1],考虑我们开始设计转移矩阵。发现里面有 max 运算和 + 运算,所以我们考虑设计一个 (max,+) 的转移矩阵。但是直接设计你发现根本不行,无法满足 + 这个运算,而且转移还带枚举所有儿子,所以考虑重新设计状态。
结合树链剖分,考虑设 gi,0 为点 i 子树内,第 i 个点的所有轻边连向的儿子都不选的最大权值,gi,1 为点 i 子树内,第 i 个点的所有轻边连向的儿子可选可不选的最大权值。fi,0/1 则是点 i 的子树内第 i 个点选/不选的最大权值,那么有:
不难发现第一个式子可以拆成 max(a+c,b+c) 的形式,显然的 (max,+) 转移形式。设矩阵为 [fi,0,fi,1],令 v=hsoni,将转移列出来:
显然 B=[fv,0,fv,1],那么可以轻松列出转移矩阵:
可以使用线段树 + 树链剖分维护一下这个矩阵。对于修改,每次计算该重链上的最大权值,然后更新转移矩阵,递归修改树链顶的父亲。询问的时候直接在根的重链上询问即可,时间复杂度为 O(k3qlog2n),其中 k=2。
(max,+) 矩阵显然存在单位矩阵 I=[0−∞−∞0]。
有一些注意的点标注在了代码上,我常数大又写的长,唉。注意这个转移时深度从下到上转移,所以线段树二区间合并时也需要反向合并,询问时也需要先询问右侧,再询问左侧。初始矩阵为 [0,0]。要记录链底。
有一些东西是讲不清楚的,具体看代码吧。
动态防洪
题意:小 A 走到一个山脚下,准备给自己造一个小屋。这时候,小 A 的朋友(op,又叫管理员)打开了创造模式,然后飞到山顶放了格水。于是小 A 面前出现了一个瀑布。作为平民的小 A 只好老实巴交地爬山堵水。那么问题来了:我们把这个瀑布看成是一个 n 个节点的树,每个节点有权值(爬上去的代价)。小 A 要选择一些节点,以其权值和作为代价将这些点删除(堵上),使得根节点与所有叶子结点不连通。问最小代价。不过到这还没结束。小 A 的朋友觉得这样子太便宜小 A 了,于是他还会不断地修改地形,使得某个节点的权值发生变化。不过到这还没结束。小 A 觉得朋友做得太绝了,于是放弃了分离所有叶子节点的方案。取而代之的是,每次他只要在某个子树中(和子树之外的点完全无关)。于是他找到你。
题面是史。
考虑最朴素的 DP:设 fi 为点 i 子树内的所有叶子节点全部不可达的最小权值和,那么有:
同样结合重剖,设 gi 为第 i 个点的轻儿子对应的所有子树的叶子节点都不可达的最小权值和,有:
然后考虑到树,DP,带修。这坨东西组合起来就是 DDP。所以考虑建出转移矩阵。
观察式子,显然是 (min,+) 转移矩阵,但是孤独一个 vi 很难处理,所以我们转移的时候把 vi 放进答案矩阵里。设每个点的矩阵为 [fi,vfai],那么同样列出转移式子:
而 B=[fhsoni,vi],那么可以轻松列出转移矩阵:
然后就是 DDP 板子题了。询问子树就询问子树的根所在的重链的链底转移到子树的根的结果就行了。但是初始矩阵好像不是简简单单 [0,0],应该是 [+∞,vp],其中 p 是叶子节点。
时间复杂度 O(k3qlog2n),其中 k=2。一堆细节,而且注意读题!
容斥优化 DP
见容斥的学习笔记,这里仅做补充。
例题:CF348D Turtles
之前在容斥后面看的卡特兰数白看了。
首先特判左上角的右与下,右下角的左与上是否有障碍,有障碍一定无解。
然后我们发现有最简单的 DP 去计算 (x1,y1)→(x2,y2) 的方案数,这里不赘述。
然后顺着上面的思路,我们只需要 DP (2,1)→(n,m−1) 和 (1,2)→(n−1,m),分别代表两只乌龟的行动路径,并把结果乘起来,但是仍然有可能路径重复。
但是路径有交点,我们可以在最后一个交点处交换两者后面的路径,发现重复的路径与 (2,1)→(n−1,m) 和 (1,2)→(n,m−1) 的乘积是等价的。
这道题就结束了,可以画图理解一下上面的一一对应关系。
SOS DP
子集 DP。
假设我们有 ai(i∈[0,2n−1]),需要求:
首先我们显然有 O(4n) 的纯暴力和 O(3n) 的枚举子集。
考虑我们使用 DP 优化这个过程,我们发现对于一个子集的求和,我们可以定住前面几个值,让它每次只变一个位置的值,就能讨论这个位置是否选择,从而求解。那么设 fi,j 为 j 的后 i 位为非固定,前 n−i 位固定时的子集和。
显然有:
下面那个式子就是讨论是否选择这一位。可以滚动 i 一维,空间复杂度为 O(2n),时间复杂度 O(n2n)。
注意初始化时按定义应该是 f0,i=ai,最后的答案就是 fn,i。
这个东西一大亮点就是不需要关注 j 的枚举顺序,考虑将 j 分为两类,一类带 2i,一类不带。这两个东西可以一一对应,所以不需要关注顺序。
注意到如果是要求:
发现超集形式其实就是每个数按位取反之后的子集结果,反映到代码上就是在判断条件上多加一个 !(),下面一样用 ^。如果之前用的是 - 就要变成 +。感觉这个硬记好一点。
例题:CF449D Jzzhu and Numbers
上来就来了一个超集形式把我整懵了。
对于理解超集形式,你可以理解为把 0 所在位当做实际位,按位取反后的子集显然就是其超集。
这道题就是这样,虽然是我为数不多的自己想出来的容斥题。
考虑定义属性 Pi 为某位上不全是 1 的方案,那么显然答案就是 |⋂20i=1Si|。转化成补集形式,变为求 |U|−|⋃20i=1¯Si|。前面那个东西就是 2n−1,后面那个东西需要容斥。如果我们知道某个值的超集的大小,这个东西对答案的贡献就是 (−1)popcount(i)(2cnt−1)。然后就用超集形式的 SOS DP 来统计某个值的超集的所有数个数。(对桶做 DP)
时间复杂度 O(nlogn)。
例题:P6442 [COCI2011-2012#6] KOŠARE
和前面那道题神似。设属性为第 i 位不全是 0 的方案,求这个东西的交就是求全集减去这个东西补集的并,即属性为第 i 位全是 0 的方案的并。和上面那道题不同,全是 0 的显然是要求子集的个数和。那么直接上 SOS DP 即可。(还是对桶 DP)
时间复杂度为 O(m2m)。
注意全 1 的贡献不能计数,因为这个东西不满足任何一个属性。还要注意计数全 0 的贡献,因为有可能出现箱子为空的情况。
例题:CF772D Varying Kibibits
非常有意思的一道题。
考虑到 min 限制非常严格,并不能从值域上入手,所以我们把 f(S)=x 的条件改一下,改成 f(S) 的每一位都不小于 x,然后就可以从值域上入手做高维前缀和了。
先不说这个前缀和的细节,不难想到换成这个条件那么我们求的 H(x) 就是:
很像一个容斥对吧。设属性为某一位不小于某一个值,那么对于 f(x),我们不难发现它的全集就是 H(x),某几位 +1 后的 H 函数值则是要容斥的贡献。但是 O(2log10nn) 的复杂度太高了(虽然能过),有没有更优秀的做法呢?
这个东西不是非常像一个高维前缀和的形式吗?那就高维差分。
考虑到从高位向低位差分,设 ti,j 为从最高位开始的前 i 位固定时,此时 j 在限制之外的超集贡献和,显然对于每一位做 ti,j←ti−1,j−ti−1,j+106−i,就能固定第 i 位。由于是减去已经固定了前 i−1 位的值,所以对已经固定的位的贡献没有影响,可以滚动,需要从小到大枚举 j。
前面你会发现光 SOS DP 并不能做,有一堆细节。
考虑我们要加入所有该位大于等于当前位的数的贡献,即:
这个东西暴力做是 O(10nlog10n) 的,比较不优,考虑优化。可以滚动,从大到小枚举 j,然后每次从 j+10i−1 转移过来。这个操作有点像一个前缀和优化 DP,你会发现每次相当于转移一个后缀,因此正确。
但是你考虑到贡献不是这么简简单单直接相加的,考虑怎么合并两个互不相交的集合的贡献。设一个集合的贡献为 c(S),再设一个集合内数的和为 sum(S),有:
然后我们分开来计算每一项到底有什么贡献。首先是 sum(x)2,这个相当于对于每一个 S 的子集元素的和的平方和(正好是 c(S))乘上 T 的子集个数,所以:
sum(y)2 同理,那一坨等于 2|S|c(T)。
最后一项 2sum(x)sum(y),就等于说是对于每一个 S 的子集,它的贡献就是它的所有子集元素和的和乘上 T 的所有子集元素和的和,所以我们再定义一个 s(x) 代表一个集合内的所有子集元素的和的和,那么这个式子就等于 2s(S)s(T)。
多了一个函数,我们就要再把这个函数对于两个集合合并的情况给讨论清楚。这里就直接给式子了,原理和上面基本一致。
所以这个 SOS DP 需要记录集合内元素个数,s 和 c 函数的值,较为复杂。
最后,我们再来讨论初始化。对于一个值 p,其对应集合 x 内有 cnt 个数 p,c(x) 和 s(x) 的值各是多少呢?对于 s(x),我们可以理解为,挑出一个数,剩下的数有 2cnt−1 种排列方案,那么这个数就贡献了 2cnt−1 次,所以 s(x)=cnt2cnt−1p,而 c(x) 就只能代数推导了。显然 c(x)=kp2,k=∑ii2(cnti)。
使用两次吸收公式:
那么预处理 2 的幂,c(x) 与 s(x) 均能 O(1) 算出。(暴力按式子求值复杂度是对的,这里推导主要是因为作者已经不想写组合数了)
那么有了上面那么多的铺垫,这道题就在 O(nlog10n) 的复杂度内做完了。
作者已经不想写代码了。/kk
例题:CF165E Compatible Numbers
SOS DP 板子题。
设状态 fj 为 j 的子集中存在的最大的一个数(其实没必要有最大的限制)。正常 DP 一遍,然后对于每一个数按位取反然后调用 f 数组即可。如果结果为 0,那么就没有数满足 aiandaj=0,如果有值,直接输出即可。时间复杂度为 O(k2k),其中 k=22。
例题:CF1679E Typical Party in Dorm
这题翻译有问题,是求对于每种填入的情况的回文子串个数的和。
这个题有点意思,等于说是对一个 struct(或者说是 int[17])进行一个高维前缀和。
首先对于原序列,n≤1000 的大小允许我们暴力 O(n2) 统计每一个子串(枚举回文中心和串长度)。我们首先来观察对于一个串回文的方案数是多少。
-
首先对于
?匹配到?的情况,需要我们从字符集里选出两个相同的值才能匹配,有 |Σ| 种情况。 -
然后是对于
?匹配到一个字符的情况,需要我们的字符集包含所匹配到的字符,有 [v∈Σ] 种情况。 -
如果是两个字符匹配,如果是两个相同字符,那么有一种情况符合,如果不相同,那么没有情况符合。
-
最后对于 [l,r] 之前统计的贡献还要再乘上 |Σ| 的 [1,l−1]∪[r+1,n] 的问号个数次方。
我们发现对于一个子串,它对答案的贡献能够写成 |Σ|k×[S⊆|Σ|] 的形式。但是字符集可能会变,所以我们对于每个串统计所有可能的字符集大小对应的答案以及每个子串能被统计所需要的条件,然后对 [S⊆|Σ|] 做高维前缀和。
在 DP 的过程中,我们对于每一种字符集大小都进行转移,所以我们设 dpk,i,j 为后 k 位放开,集合为 i,实际字符集大小为 j 时的贡献和。最后我们对于一个询问,输出 dp17,Σ,|Σ| 的值即可。
时间复杂度 O(|Σ|22|Σ|+|Σ|n2+|Σ|q)。
缩点 DP
最后一种 DP 了,有点开心。
对于有向图上 DP,我们可以缩点在 DAG 上 DP。对于无向图,我们可以建圆方树或者求边双连通分量把图变成一个树,然后 DP。
例题:P2656 采蘑菇
对于每个点计算其在经过 +∞ 步后一共能摘到多少蘑菇,这一个过程可以在 O(mlogV) 的时间复杂度内计算。
然后缩点后从 S 开始跑一遍最长路就行了。可以先 DFS 一遍看哪些点可以由 S 到,然后把这些点提出来跑一遍拓扑排序。
图论知识忘完了。/ll
例题:P2515 [HAOI2010] 软件安装
发现对于环,只有全部选才能满足,那么把所有环缩成点,重量和价值累加。
然后剩下的元素组成一个森林,对于每一个弱连通块,如果要选一个点,那么一定要选这个点到根的所有元素。那么对于一个点的儿子的 DP 数组全部暴力 (max,+) 卷起来,然后把整个数组向后平移 wi 个元素,然后把 [wi,m] 的所有元素加上 vi。
最后把所有弱连通块的贡献 (max,+) 卷起来即可。时间复杂度 O(m2n)。
终于结束了。
后记
这个东西作者整了 2 个月,非常累。
来路还很长,考虑到就 DP 而言,我们还有 wqs 二分,图上 DP(比如什么耳分解之类的),轮廓线 DP,(基环)树 DP,仙人掌 DP,计数 DP,期望 DP,DP 套 DP,等等。
我的 OI 生涯还有几个 2 个月呢?
本文作者:xingyu_xuan
本文链接:https://www.cnblogs.com/xingyuxuan/p/18357229
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步