DP(一)
前言
习题博客:link。
因为各种原因,这个博客是赶出来的,所以大概率会有没讲清楚或者讲错了的情况,请大家及时指出。
因为个人不是非常擅长于 DP,可能很难判别一道题的好坏,所以可能存在几道史题在题单中,请大家谅解。
这篇博客理论上仅限于讲解例题,大部分习题的题解请移步至配套博客查看。关于习题:就是我认为大家做完上一道题之后能自己做出来的题。
那么就让我们开始吧。
UPD:该课件计划加入 DP 杂题部分,这样的话这个课件就理论上会一直更新下去。
DP 是什么
DP(Dynamic Programming),动态规划,通常用于处理最优性问题,也可以用来计数等。其核心思想就是设置状态,使得这些状态能够进行转移,最后得出结果。
另一种理解方式就是,DP 能够通过设置状态转移的方式来缩小问题规模,就比如我们推出了一个从前 个物品转移到前 个物品的转移式,我们就成功把问题规模从 变成了 ,因为这里存在一个从 到 的递推关系。
DP 优于暴力就是因为,暴力的时候,我们其实会重复处理很多信息,而 DP 通过设置状态并储存状态信息来进行一个类似于记忆化的过程,从而省去了很多很多重复的计算。
举一个非常简单的例子:
最长公共子序列问题:
给定两个串 ,可以删除 中的一些元素,将 中剩下元素按原顺序拼在一起组成串 ;对 进行一样的操作得到 ,求最长的 的长度 使得 。
我们可以设置状态 代表这个最长的子序列放到 的原位置中最后位置的下标 ,放到 的原位置中最后位置的下标 时的最长子序列长度。我们发现有转移:
这样我们可以在 的时间复杂度内解决这个问题。这比暴力的 好多了。
DP 的前置条件
能用 DP 解决的问题通常需要满足三个条件,即最优子结构,无后效性,子问题重叠。
- 最优子结构
这个指子问题的最优解能够转移到原问题的最优解。满足这个条件的问题有些时候也可以用贪心做。
- 无后效性
前面子问题的解不会受后面决策的影响。
- 子问题重叠
如果没有重叠的子问题,那么 DP 其实和暴力是等复杂度的。
对于大多数题,如果计算的贡献完整且没有重复,然后无后效性,这个 DP 大概率就是正确的。
朴素 DP
就是什么特殊类 DP 都不是的纯暴力 DP,放到开头给大家练练手。
例题:CF1096D Easy Problem
*1800,想必大家都能独立切掉。
给你一个长为 的字符串 以及 ,删去第 个字符的代价为 ,你需要删去一些字符(如果一开始就符合条件当然可以不删)使得剩下的串中不含子序列 "hard",求最小代价。
子序列不需要连续。
。
题解
我们设状态 表示前 个字符中,hard 仅前 个字符已经匹配完成的最小代价。
转移是简单的。如果当前位是 h,那么有:
第一个式子代表不删这个 h 时的转移,第二个式子则代表删掉这个 h 之后的转移。
当前位为其他值类似,最后的答案就是 。时间复杂度为 。空间可以滚动。
代码
#include<bits/stdc++.h>
using namespace std;
int n;
char s[100005];
long long f[100005][4];
int a[100005];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
memset(f,0x3f,sizeof f);
f[0][0]=0;
cin>>n;
for(int i=1;i<=n;i++)cin>>s[i];
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++){
for(int j=0;j<=3;j++)f[i][j]=f[i-1][j];
if(s[i]=='h')f[i][1]=min(f[i][1],f[i-1][0]),f[i][0]=f[i-1][0]+a[i];
else if(s[i]=='a')f[i][2]=min(f[i][2],f[i-1][1]),f[i][1]=f[i-1][1]+a[i];
else if(s[i]=='r')f[i][3]=min(f[i][3],f[i-1][2]),f[i][2]=f[i-1][2]+a[i];
else if(s[i]=='d')f[i][3]=f[i-1][3]+a[i];
}
cout<<min({f[n][0],f[n][1],f[n][2],f[n][3]});
return 0;
}
例题:P1410 子序列
要想学好 DP,首先要练习如何吃史。
给定一个长度为 ( 为偶数)的序列,问能否将其划分为两个长度为 的严格递增子序列。
。
题解
这题的状态设计非常神秘。
设 为前 个元素可以拆成两个递增子序列,第一个的长度为 ,并且最后一位对应的下标是 ,第二个的最大值的最小值。
因为存的是最小值,我们就能较为方便的转移。
假设下一个元素 的值 ,那么这里可以直接扩展第二个子序列,有 。
如果 ,这里也可以直接扩展第一个子序列,有 。
其他情况均不能扩展任何子序列。
最后判定 是不是 就行了。
最初做这道题的时候,作者认为这道题非常史。
代码
#include<bits/stdc++.h>
using namespace std;
int f[2005][2005];
int a[2005];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int n;
while(cin>>n){
for(int i=1;i<=n;i++)cin>>a[i];
memset(f,0x3f,sizeof f);
f[1][1]=0;
for(int i=1;i<n;i++){
for(int j=1;j<=i;j++){
if(a[i+1]>f[i][j])f[i+1][i-j+1]=min(f[i+1][i-j+1],a[i]);
if(a[i+1]>a[i])f[i+1][j+1]=min(f[i+1][j+1],f[i][j]);
}
}
if(f[n][n/2]<=1000000000)cout<<"Yes!\n";
else cout<<"No!\n";
}
return 0;
}
顺带一提,这题有双倍经验 P4728。
选做题:P4740 [CERC2017] Embedding Enumeration
作者认为,分讨是 DP 的一大重点。
输入一棵有标号树,求把这棵树放入 的网格图中的方案数,对 取模。
两种方案相同当且仅当网格图内标号分布完全相同。
要求: 必须放在 ,有边连接的节点必须相邻,两个节点不能放在同一个格子。
。
Hint
大家可以尝试直接对某个节点在左上角时的方案数进行分类讨论。
题解
作者的分类讨论和代码都非常复杂,仅供参考!!!
另外,因为这个题调不出来会很难受,所以作者提供数据,内网,外网。
设 为树上的点 在左上角时放 的子树的方案数。
有 种大情况:
第一种:
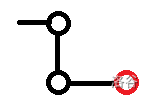
注意到这里的左上角黑点不一定就是 ,也有可能是 的子孙。注意这个子孙到 中间经过的所有点度数为 ,否则会和下面的情况重复一些。
这个时候的贡献就是红色的点的 DP 值,我们需要记录树上的这种链(链顶到链底的父亲都只有一个儿子)的 DP 值和。
第二种:
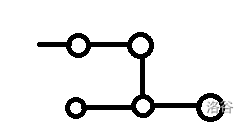
需要判断左下链的合法性,贡献为右下的点的 DP 值。
第三种:
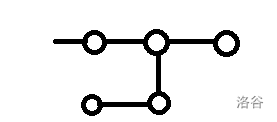
下面的子树可以往左摆或者往右摆。
向左摆是简单的,但是向右摆的话就要满足这两棵子树中至少有一个是链,贡献就是某个子树第一次超过另外一个链的点的 DP 值,没有超过也有 的贡献。
这里可能需要记录 DFS 序来实现 转移。
注意如果下面的子树大小就只有 ,注意向左摆和向右摆只能算一个,不然会算重。
第四种:
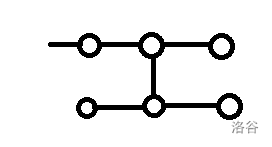
这里有三个子树,我们把左下子树称为 子树,右下子树称为 子树,右上子树称为 子树。
显然 子树一定是链,我们只用保证 子树其中有至少一个是链就行了,贡献和第三种是一致的。
注意如果 的子树就是链,还要特判一条直链,一条直链最后拐下来一格,还有拐下来后只往左摆。
可能还要特判 有两个儿子的情况。
作者的实现非常史,代码中分了 种情况,其中 Situation 1 对应这里的第一种情况;Situation 2 对应这里的第二种情况;Situation 3-5 对应这里的第三种情况;Situation 6 对应这里的第四种情况;Situation 7 说的是一条链拐下来之后向左摆(摆的长度 )的情况。
代码
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
#define int long long
vector<int> son[300005];
int f[300005],fa[300005],sum[300005],len[300005],edid[300005];
int tst[300005],dfn[300005],rk[300005],dfncnt;
vector<int> to[300005];
void init(int now,int f){
fa[now]=f;
dfn[now]=++dfncnt;
rk[dfncnt]=now;
for(auto v:to[now]){
if(v^f){
son[now].push_back(v);
init(v,now);
}
}
if(son[now].size()==1){
len[now]=len[son[now][0]]+1;
edid[now]=edid[son[now][0]];
if(!edid[now])edid[now]=son[now][0];
tst[now]=tst[son[now][0]];
}else if(son[now].size()==2)tst[now]=1,edid[now]=now;
else if(son[now].size()>2){
cout<<0;
exit(0);
}
return;
}
int n,x,y;
void dfs(int now){
for(auto v:son[now])dfs(v);
int &p=f[now];
//Situation 1
if(len[now]>=2)p=(p+sum[son[son[now][0]][0]]);
//Situation 7
if(!tst[now]&&len[now]>=3)p=(p+len[now]-2-(len[now]/2)+1)%mod;
//SP-Straight segment
if(!tst[now])p=(p+1)%mod;
//SP-len>=1
// ------
// |
if(!tst[now]&&len[now]>=1)p=(p+1)%mod;
//Situation 2-6
if(tst[now]){
//get next deg-3 point
int nxt3=edid[now];
//SP-now is deg-3 point
if(nxt3==now){
//sub1:2 segments
if(!tst[son[now][0]]&&!tst[son[now][1]]){
int mx=len[son[now][0]]>len[son[now][1]]?son[now][0]:son[now][1];
int mi=mx==son[now][0]?son[now][1]:son[now][0];
p=(p+f[rk[dfn[mx]+len[mi]]])%mod;
if(len[mx]>len[mi]+1)p=(p+f[rk[dfn[mx]+len[mi]+2]]%mod)%mod;
else p=(p+1)%mod;
}//sub2:1 tree,1 segment
else if(tst[son[now][0]]+tst[son[now][1]]==1){
int _1=tst[son[now][0]]==1?son[now][0]:son[now][1];
int _0=tst[son[now][0]]==0?son[now][0]:son[now][1];
if(len[_1]>=len[_0])p=(p+f[rk[dfn[_1]+len[_0]]])%mod;
if(len[_1]>=len[_0]+2)p=(p+f[rk[dfn[_1]+len[_0]+2]])%mod;
}
}else{
//Situation 2
if(dfn[nxt3]-dfn[now]>=2){
int nxtlen=dfn[nxt3]-dfn[now]-1;
if(!tst[son[nxt3][0]]&&len[son[nxt3][0]]<nxtlen)p=(p+f[son[nxt3][1]])%mod;
if(!tst[son[nxt3][1]]&&len[son[nxt3][1]]<nxtlen)p=(p+f[son[nxt3][0]])%mod;
}
//Situation 3
if(!tst[son[nxt3][0]]&&!tst[son[nxt3][1]]){
//Copy upper code-deal RR situation
int mx=len[son[nxt3][0]]>len[son[nxt3][1]]?son[nxt3][0]:son[nxt3][1];
int mi=mx==son[nxt3][0]?son[nxt3][1]:son[nxt3][0];
p=(p+f[rk[dfn[mx]+len[mi]]])%mod;
if(len[mx]>len[mi]+1)p=(p+f[rk[dfn[mx]+len[mi]+2]])%mod;
else p=(p+1)%mod;
//deal LR situation
if(len[now]>=len[mi]&&len[mi]!=0)p=(p+f[mx])%mod;
if(len[now]>=len[mx]&&len[mx]!=0)p=(p+f[mi])%mod;
}
//Situation 4-5
if(tst[son[nxt3][0]]+tst[son[nxt3][1]]==1){
int mx=tst[son[nxt3][0]]?son[nxt3][0]:son[nxt3][1];
int mi=mx==son[nxt3][0]?son[nxt3][1]:son[nxt3][0];
//Situation 4
if(len[mi]<=len[now]&&len[mi]!=0)p=(p+f[mx])%mod;
if(len[mx]>=len[mi])p=(p+f[rk[dfn[mx]+len[mi]]]%mod)%mod;
//Situation 5
if(len[mx]>=len[mi]+2)p=(p+f[rk[dfn[mx]+len[mi]+2]]%mod)%mod;
}
//Situation 6
// -------
// |
// -------
//shape
//this is a large situation!!!
if(max(son[son[nxt3][0]].size(),son[son[nxt3][1]].size())==2&&son[son[nxt3][0]].size()+son[son[nxt3][1]].size()<=3){
int mx=son[son[nxt3][0]].size()==2?son[nxt3][0]:son[nxt3][1];
int mi=mx==son[nxt3][0]?son[nxt3][1]:son[nxt3][0];
int _1=mi,_2=son[mx][0],_3=son[mx][1];
//sub1: 3 segments
if(tst[_1]+tst[_2]+tst[_3]==0){
if(len[now]>len[_2]){
int __1=len[_1]>len[_3]?_1:_3;
int __2=len[_1]<len[_3]?_1:_3;
if(len[__1]==len[__2])p=(p+1)%mod;
else p=(p+f[rk[dfn[__1]+len[__2]+1]])%mod;
}
if(len[now]>len[_3]){
int __1=len[_1]>len[_2]?_1:_2;
int __2=len[_1]<len[_2]?_1:_2;
if(len[__1]==len[__2])p=(p+1)%mod;
else p=(p+f[rk[dfn[__1]+len[__2]+1]])%mod;
}
}
//sub2: 2 segments 1 tree
if(tst[_1]+tst[_2]+tst[_3]==1){
if(tst[_1]==1){
if(len[_2]<len[now]&&len[_3]<len[_1])p=(p+f[rk[dfn[_1]+len[_3]+1]])%mod;
if(len[_3]<len[now]&&len[_2]<len[_1])p=(p+f[rk[dfn[_1]+len[_2]+1]])%mod;
}else{
if(tst[_2]!=1)swap(_2,_3);
if(len[_3]<len[now]&&len[_1]<len[_2])p=(p+f[rk[dfn[_2]+len[_1]+1]])%mod;
}
}
}
}
}
sum[now]=f[now];
if(son[now].size()==1)sum[now]=(sum[now]+sum[son[now][0]])%mod;
return;
}
signed main(){
f[0]=1;
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<n;i++)cin>>x>>y,to[x].push_back(y),to[y].push_back(x);
init(1,0);
dfs(1);
cout<<f[1];
return 0;
}
这里有一道据说类似的题,如果感兴趣可以做做。
区间 DP
区间 DP,就是指状态中含有一个区间的 DP,使用时通常需要满足可以快速加入元素或可以快速合并,大多数题都是从小区间转移到大区间。
因为合并区间时会枚举决策点,这个时候可以使用一些有关决策的 DP 优化,但是这目前不在我们的讨论范围之内。
如果用区间 DP 计数的时候,注意去重。
由于作者认为这个 DP 比较重要,所以塞了比较多题。
接下来就是例题时间了。
P7914 [CSP-S 2021] 括号序列
具体而言,小 w 定义“超级括号序列”是由字符
(、)、*组成的字符串,并且对于某个给定的常数 ,给出了“符合规范的超级括号序列”的定义如下:
()、(S)均是符合规范的超级括号序列,其中S表示任意一个仅由不超过 个字符*组成的非空字符串(以下两条规则中的S均为此含义);- 如果字符串
A和B均为符合规范的超级括号序列,那么字符串AB、ASB均为符合规范的超级括号序列,其中AB表示把字符串A和字符串B拼接在一起形成的字符串;- 如果字符串
A为符合规范的超级括号序列,那么字符串(A)、(SA)、(AS)均为符合规范的超级括号序列。- 所有符合规范的超级括号序列均可通过上述 3 条规则得到。
例如,若 ,则字符串
((**()*(*))*)(***)是符合规范的超级括号序列,但字符串*()、(*()*)、((**))*)、(****(*))均不是。特别地,空字符串也不被视为符合规范的超级括号序列。现在给出一个长度为 的超级括号序列,其中有一些位置的字符已经确定,另外一些位置的字符尚未确定(用
?表示)。小 w 希望能计算出:有多少种将所有尚未确定的字符一一确定的方法,使得得到的字符串是一个符合规范的超级括号序列?。
Hint
如果不好去重,就多定义几个状态出来辅助 DP 来去掉去重这一步。
题解
这里讲一种不需要去重的 DP 方式。
首先我们可以预处理出那些区间是可以变成 S 的。
设 为该区间字符串是超级括号序列的方案数, 代表该区间字符串为 SA(A 是超级括号序列)的方案数, 代表该区间字符串为 AS 的方案数, 代表该区间字符串是 () 或 (S) 或 (AS) 或 (SA) 或 (A) 的方案数。
首先看 怎么转移。我们肯定是枚举 S 的长度,然后再后边尝试接上一个 A,不难发现其实是不会有算重的情况的, 也是类似。
然后考虑怎么转移 。首先可以特判 () 和 (S) 的情况,然后 (AS) 和 (SA) 其实都可以直接通过 和 转移过来。
最后就是最难的 了。最简单的转移是 ,然后我们考虑 ASB,发现其实可以直接 ,这样是不会重复的,因为 S 的起点在每次转移的时候都不同。最后我们考虑 AB,我们发现如果直接 是不可行的,因为显然此时假如说这个区间存在一种由 个 (...) 用 AB 方式组合起来的方案,那么这样计算这种方案就被计算了 次。考虑每种方案只有一个最左边的 (...),所以 就是正确的了(这里代码中写的是 )。
代码
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
#define int long long
int n,k;
int S[502][502];
char s[505];
int f[505][505],g[505][505],h[505][505],whol[505][505];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>s[i];
for(int i=1;i<=n;i++){
for(int j=i;j<=min(n,i+k-1);j++){
//[i,j]
if(s[j]=='*'||s[j]=='?')S[i][j]=1;
else break;
}
}
for(int i=1;i<n;i++){
if((s[i]=='?'||s[i]=='(')&&(s[i+1]=='?'||s[i+1]==')'))whol[i][i+1]=1;
for(int j=i+2;j<=min(n,i+k+1);j++){
if((s[i]=='?'||s[i]=='(')&&(s[j]=='?'||s[j]==')')&&S[i+1][j-1])whol[i][j]=1;
}
}
for(int i=2;i<=n;i++){
for(int j=1;j<=n-i+1;j++){
for(int p=j;p<j+i-1;p++){
f[j][j+i-1]=(f[j][j+i-1]+whol[j][p]*(f[p+1][j+i-1]+g[p+1][j+i-1])%mod)%mod;
g[j][j+i-1]=(g[j][j+i-1]+S[j][p]*f[p+1][j+i-1])%mod;
h[j][j+i-1]=(h[j][j+i-1]+S[p+1][j+i-1]*f[j][p])%mod;
}
if((s[j]=='?'||s[j]=='(')&&(s[j+i-1]=='?'||s[j+i-1]==')'))whol[j][j+i-1]=(whol[j][j+i-1]+f[j+1][j+i-2]+g[j+1][j+i-2]+h[j+1][j+i-2])%mod;
f[j][j+i-1]=(f[j][j+i-1]+whol[j][j+i-1])%mod;
}
}
cout<<f[1][n];
return 0;
}
UVA1630 串折叠 Folding
折叠由大写字母组成的长度为 ()的一个字符串,使得其成为一个尽量短的字符串,例如
AAAAAA变成6(A)。
这个折叠是可以嵌套的,例如NEEEEERYESYESYESNEEEEERYESYESYES会变成2(N5(E)R3(YES))。
多解时可以输出任意解。。
输出方案的题是逃避不了的/xk。
如果大家写挂了,可以先到这道题来检验 DP 的正确性。
题解
这题我直接写从最短的循环节转移就过了,然后我和 zfy 讨论能不能从最短的循环节转移过来,最后 zfy 说自己证出来可以,但是我不太知道原理。
这题其实比较简单。
设 为区间 的答案,可以从枚举循环节转移,也可以两区间合并。
暴力枚举循环节复杂度是 ,所以总复杂度是 。
方案的话,记录这个是从循环节还是区间转移过来的,记录决策点,最后 DFS 还原即可。
代码
#include<bits/stdc++.h>
using namespace std;
int dp[101][101],g[101][101];
char s[101],*ss=s+1;
const int SIG=1e5;
int _10[101];
string getans(int l,int r){
// cerr<<l<<" "<<r<<"\n";
if(!g[l][r]){
string tmp;
tmp.clear();
for(int i=l;i<=r;i++)tmp+=s[i];
return tmp;
}
if(g[l][r]>SIG){
string tmp;
tmp.clear();
tmp+=to_string((r-l+1)/(g[l][r]-SIG-l+1));
tmp+='(';
tmp+=getans(l,g[l][r]-SIG);
tmp+=')';
return tmp;
}
return getans(l,g[l][r])+getans(g[l][r]+1,r);
}
#define ull unsigned long long
ull hsh[105],_b[105];
const ull base=179;
ull gethsh(int l,int r){
return hsh[r]-hsh[l-1]*_b[r-l+1];
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
for(int i=1;i<=9;i++)_10[i]=1;
for(int i=10;i<=100;i++)_10[i]=_10[i/10]+1;
_b[0]=1;
for(int i=1;i<=100;i++)_b[i]=_b[i-1]*base;
while(cin>>ss){
memset(g,0,sizeof g);
int n=strlen(ss);
for(int i=1;i<=n;i++)hsh[i]=hsh[i-1]*base+s[i]-'A'+1;
for(int i=1;i<=n;i++)for(int j=i;j<=n;j++)dp[i][j]=j-i+1;
for(int i=2;i<=n;i++){
for(int j=1;j<=n-i+1;j++){
for(int k=j;k<j+i-1;k++){
if(dp[j][j+i-1]>dp[j][k]+dp[k+1][j+i-1]){
g[j][j+i-1]=k;
dp[j][j+i-1]=dp[j][k]+dp[k+1][j+i-1];
}
if(i%(k-j+1))continue;
//[j,k]
bool flag=1;
for(int o=j;o<=j+i-1&&flag;o+=k-j+1){
flag&=gethsh(j,k)==gethsh(o,o+k-j);
}
if(flag){
if(dp[j][j+i-1]>_10[i/(k-j+1)]+2+dp[j][k]){
g[j][j+i-1]=SIG+k;
dp[j][j+i-1]=_10[i/(k-j+1)]+2+dp[j][k];
}
}
}
}
}
// cout<<dp[1][n]<<"\n";
cout<<getans(1,n)<<"\n";
}
return 0;
}
有兴趣的可以再来做一道字符串压缩的题,这道题感觉比较有意思:[AGC020E] Encoding Subsets。
P4766 [CERC2014] Outer space invaders
来自外太空的外星人(最终)入侵了地球。保卫自己,或者解体,被他们同化,或者成为食物。迄今为止,我们无法确定。
外星人遵循已知的攻击模式。有 个外星人进攻,第 个进攻的外星人会在时间 出现,距离你的距离为 ,它必须在时间 前被消灭,否则被消灭的会是你。
你的武器是一个区域冲击波器,可以设置任何给定的功率。如果被设置了功率 ,它会瞬间摧毁与你的距离在 以内的所有外星人(可以等于),同时它也会消耗 单位的燃料电池。
求摧毁所有外星人的最低成本(消耗多少燃料电池),同时保证自己的生命安全。
。
Hint
如果发现不好想转移的话,可以想想什么是这个区间一定会执行的操作。
题解
首先不难发现这个时间是可以离散化的,这样我们就可以设 是消灭生存区间的两个端点都在 内的最低成本。
直接想转移可能比较困难。考虑什么东西是这个区间的答案一定含有的。
不难发现想要消灭这个区间内的所有外星人,最优情况下我们一定有一次选择了 的功率进行消灭。我们可以在 的时间内找到这个外星人。
因为我们一定会在这个外星人的生存区间中的一个点发动 的攻击,所以我们可以枚举在这个生存区间的哪个位置发动这个攻击。因为这是整个区间的最大功率,所以它一定也会消灭所有生存区间跨过这个位置的外星人,这个时候就只剩下左右两个区间内的外星人了。我们可以列出方程式(设 是距离最远的那个外星人的编号):
时间复杂度 。
代码
#include<bits/stdc++.h>
using namespace std;
int T,n,dis[505],l[505],r[505],maxid[605][605],dp[605][605];
int num[605],kcnt;
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>T;
while(T--){
cin>>n;
kcnt=0;
memset(maxid,0,sizeof maxid);
for(int i=1;i<=n;i++){
cin>>l[i]>>r[i]>>dis[i];
num[++kcnt]=l[i];
num[++kcnt]=r[i];
}
sort(num+1,num+kcnt+1);
kcnt=unique(num+1,num+kcnt+1)-num-1;
for(int i=1;i<=n;i++){
l[i]=lower_bound(num+1,num+kcnt+1,l[i])-num;
r[i]=lower_bound(num+1,num+kcnt+1,r[i])-num;
}
for(int i=1;i<=kcnt;i++){
for(int j=i+1;j<=kcnt;j++){
for(int p=1;p<=n;p++){
if(l[p]>=i&&r[p]<=j)if(dis[p]>dis[maxid[i][j]])maxid[i][j]=p;
}
}
}
for(int i=1;i<=kcnt;i++)for(int j=i+1;j<=kcnt;j++)dp[i][j]=1e9;
for(int i=2;i<=kcnt;i++){
for(int j=1;j<=kcnt-i+1;j++){
//[j,j+i-1]
int id=maxid[j][j+i-1];
if(!id){dp[j][j+i-1]=0;continue;}
for(int k=l[id];k<=r[id];k++){
dp[j][j+i-1]=min(dp[j][j+i-1],dp[j][k-1]+dp[k+1][j+i-1]+dis[id]);
}
}
}
cout<<dp[1][kcnt]<<"\n";
}
return 0;
}
选做习题:P3592 [POI2015] MYJ
P2339 [USACO04OPEN] Turning in Homework G
贝茜有 ( ) 门科目的作业要上交,之后她要去坐巴士和奶牛同学回家。
每门科目的老师所在的教室排列在一条长为 ( ) 的走廊上,他们只在课后接收作业,交作业不需要时间。贝茜现在在位置 0,她会告诉你每个教室所在的位置,以及走廊出口的位置。她每走 1 个单位的路程,就要用 1 秒。她希望你计算最快多久以后她能交完作业并到达出口。
Hint
这道题不难发现先交一个区间的作业不能作为状态,因为有可能在等区间内的老师下课的时候可以跑到区间外交作业。那有没有可能先不交一个区间的作业作为状态呢?
题解
设 为区间 的作业还没交,当前在 位置还是 位置的最小时间。
非常反直觉的状态设计对吧?如何证明其包含最优解呢?考虑把最优解倒过来看,这样我们可以把下课变成上课,即需要在上课之前交作业。这个时候的 DP 就是枚举交了哪个区间的作业,现在在该区间的左端点还是右端点,求最小时间。把这个 DP 再倒过来就变成上面的状态了,两个都是最小时间没有问题,因为这两个最小时间加起来就等于最优解时间。
另一种理解方式就是,如果 位置的作业之前没交,你移动到 之后要走回来交;如果 位置的作业之前可以交,那么完全可以先移动到 之后再移动。所以转移是完整的。
剩下的转移也非常简单了,从大区间转移到小区间,枚举上次移动是从左边还是右边移动过来即可。注意没有下课的时候需要等待,在倒过来的 DP 中这一步就代表这个地方已经上课了,需要增加最优解时间来使得其延后上课。
时间复杂度 。
如果实在理解不了,你也可以在外面套个二分,因为答案具有单调性。然后倒着 DP 检验即可,时间复杂度 。
代码
#include<bits/stdc++.h>
using namespace std;
int n,h,b;
int x[1005],t[1005];
int id[1005];
int dp[1005][1005][2];
int main(){
ios::sync_with_stdio(0);
cin>>n>>h>>b;
h++;
b++;
int acth=0;
for(int i=1;i<=n;i++){
cin>>x[i]>>t[i];
x[i]++;
acth=max(x[i],acth);
if(t[id[x[i]]]<t[i])id[x[i]]=i;
}
h=acth;
memset(dp,0x3f,sizeof dp);
dp[1][h][0]=0;
dp[1][h][1]=h-1;
for(int i=h-1;i>=1;i--){
for(int j=1;j<=h-i+1;j++){
//[j,j+i-1]
dp[j][j+i-1][1]=min(max(dp[j][j+i][1],t[id[j+i]])+1,max(dp[j-1][j+i-1][0],t[id[j-1]])+i);
dp[j][j+i-1][0]=min(max(dp[j-1][j+i-1][0],t[id[j-1]])+1,max(dp[j][j+i][1],t[id[j+i]])+i);
}
}
int ans=1e9;
for(int i=1;i<=h;i++){
ans=min(ans,max(dp[i][i][0],t[id[i]])+abs(b-i));
}
cout<<ans;
return 0;
}
P9746 「KDOI-06-S」合并序列
注意:该题为选做题。
给定一个长度为 的序列 。
你可以对这个序列进行若干(可能为 )次操作。在每次操作中,你将会:
选择三个正整数 ,满足 且 的值不超过此时序列的长度。记 。
然后,删除 ,并在原来这 个数所在的位置插入 。注意,此时序列 的长度将会减少 。
请你判断是否能够使得序列 仅剩一个数,也就是说,在所有操作结束后 的长度为 。若可以,你还需要给出一种操作方案。
,。
Hint
大家可以尝试多建几个数组来在 DP 的时候分步合并转移。
题解
以下令 。
转换一下题意,设 为区间 是否可以被消成一个数,如果需要让 ,那么我们需要满足存在 ,使得 且 。
首先肯定可以先 预处理出所有区间的异或和,然后直接暴力枚举 ,时间复杂度 。
我们的目标是 ,所以我们要把这 个维度的枚举变成 个维度的枚举,想到分步转移。假设最后枚举 ,我们可以设 代表满足 的最小的 。这个时候还需要枚举 个维度,于是继续压。因为求的已经是最小的 了,为了方便就只能枚举 。于是我们再设 表示满足 的最小的 ,这样我们就可以 转移了。
输出方案的时候,转移 的时候记录 ,转移 的时候记录 ,转移 的时候记录 即可。时间复杂度 。
因为这题是可以通过 的信息转移到 上,所以转移顺序应该是倒序枚举 再枚举 ,根据第二个转移,我们需要顺序枚举 ,因为 的右端点一定不会贡献 的值。
交一发之后发现 T 在了 hack 数据,我们需要减小常数。
我们发现第一个转移 的部分可以变成最后在转移完 的时候进行 。这样能减少 左右的常数,可以通过。
代码
#include<bits/stdc++.h>
using namespace std;
int T,n;
int a[505];
int xors[505][505];
int h[505][515],g[505][515];
bool f[505][505];
int posh[505][515],posg[505][515],posf[505][505];
const int M=512;
struct op{
int i,j,k;
};
vector<op> ans;
void getans(int l,int r){
// cerr<<l<<" "<<r<<" "<<f[l][r]<<"\n";
if(l==r)return;
int d=posf[l][r];
int a=posg[l][xors[d][r]];
int b=posh[a][xors[d][r]^xors[l][a]];
int c=g[l][xors[d][r]];
getans(d,r);
getans(b,c);
getans(l,a);
ans.push_back((op){l,b-(a-l),d-(a-l)-(c-b)});
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>T;
int n;
while(T--){
memset(h,0x3f,sizeof h);
memset(g,0x3f,sizeof g);
memset(f,0,sizeof f);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++){
int tmp=0;
for(int j=i;j<=n;j++){
tmp^=a[j];
xors[i][j]=tmp;
}
}
for(int i=1;i<=n;i++)f[i][i]=1;
for(int i=n;i>=1;i--){
int l=i;
for(int j=i;j<=n;j++){
int r=j;
int tmp=0;
for(int k=r;k>l;k--){
tmp^=a[k];
if(g[l][tmp]<k&&f[k][r]){
f[l][r]=1;
posf[l][r]=k;
break;
}
}
if(f[l][r]){
if(h[l-1][xors[l][r]]>r)h[l-1][xors[l][r]]=r,posh[l-1][xors[l][r]]=l;
for(int i=0;i<M;i++){
if(g[l][i]>h[r][i^xors[l][r]])g[l][i]=h[r][i^xors[l][r]],posg[l][i]=r;
}
}
}
for(int i=0;i<M;i++)if(h[l-1][i]>h[l][i])h[l-1][i]=h[l][i],posh[l-1][i]=posh[l][i];
}
if(!f[1][n])cout<<"Shuiniao\n";
else{
// cerr<<f[2][4]<<"\n";
cout<<"Huoyu\n";
getans(1,n);
cout<<ans.size()<<"\n";
for(auto p:ans)cout<<p.i<<" "<<p.j<<" "<<p.k<<"\n";
ans.clear();
}
}
return 0;
}
P3607 [USACO17JAN] Subsequence Reversal P
给你一个长度为 的序列 ,求翻转一个子序列之后最长的不下降子序列长度。
。
Hint
尝试转化(或拆)一下翻转子序列这个操作呢?
题解
把翻转子序列这个操作拆成交换几个元素对,这些元素对满足两两均有包含关系。根据这个 包含关系,我们知道这道题是显然可以区间 DP 的。
所以我们设 为区间 中的所有元素值在 的最长子序列长度。枚举翻转和扩展的所有情况,转移较为容易,这里就不展开叙述。注意几个点就行了:
- 枚举翻转的时候不止可以转移两边都能扩展的子序列。
- 注意在 内,所以这里要取一个类似于二维前缀 的东西。
代码
#include<bits/stdc++.h>
using namespace std;
int f[55][55][55][55];
int n;
const int m=50;
int a[55];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++){
for(int l=1;l<=m;l++){
for(int r=1;r<=m;r++){
if(l<=a[i]&&r>=a[i])f[i][i][l][r]=1;
}
}
}
for(int i=2;i<=n;i++){
for(int j=1;j<=n-i+1;j++){
//[j,j+i-1]
if(a[j]>a[j+i-1]){
//swap j j+i-1
f[j][j+i-1][a[j+i-1]][a[j]]=2+f[j+1][j+i-2][a[j+i-1]][a[j]];
}
for(int p=max(a[j],a[j+i-1])+1;p<=m;p++)f[j][j+i-1][a[j+i-1]][p]=1+f[j+1][j+i-2][a[j+i-1]][p];
for(int p=min(a[j],a[j+i-1])-1;p>=1;p--)f[j][j+i-1][p][a[j]]=1+f[j+1][j+i-2][p][a[j]];
for(int p=1;p<=m;p++){
for(int l=1;l<=m-p+1;l++){
int r=l+p-1;
//[j,j+i-1],[l,r]
f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j+1][j+i-1][l][r]);
if(l<=a[j]&&a[j]<=r)f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j+1][j+i-1][a[j]][r]+1);
// if(j==1&&j+i-1==2)cerr<<j<<" "<<j+i-1<<" "<<l<<" "<<r<<" "<<f[j][j+i-1][l][r]<<" "<<a[j]<<"\n";
f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j][j+i-2][l][r]);
if(r>=a[j+i-1]&&l<=a[j+i-1])f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j][j+i-2][l][a[j+i-1]]+1);
f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j][j+i-1][l][r-1]);
f[j][j+i-1][l][r]=max(f[j][j+i-1][l][r],f[j][j+i-1][l+1][r]);
}
}
}
}
cout<<f[1][n][1][m];
return 0;
}
P10041 [CCPC 2023 北京市赛] 史莱姆工厂
有 个史莱姆排成一行,其中第 个的颜色为 ,质量为 。
你可以执行任意次把一个史莱姆的质量增加 的操作,需要花费 的价钱。
但是一旦史莱姆的质量达到 或以上,就会变得不稳定而必须在下一次操作之前被卖掉。你只能卖出质量大于等于 的史莱姆。根据市场价,卖掉一个质量为 的史莱姆可以得到 的收入。保证 。但不保证 单调不降。
卖掉一个史莱姆之后,它两边的史莱姆会被挤压继而靠在一起。如果这两个史莱姆颜色相同,那么就会互相融合成一个史莱姆,其质量是二者的质量之和。这个新的史莱姆也有可能需要被卖掉从而接着进行这个过程。
你想知道卖掉所有史莱姆最多可以净赚多少。
,。
区间 DP 魔王。(仅凭洛谷评级来看)
Hint
对于一个区间,想想最后一个操作会发生在哪里,然后尝试把这个操作钦定发生在一个区间内的特殊的位置。
题解
参考了部分 Hanghang 的题解,但是 Hanghang 的题解中有些错误,怎么回事捏。
考虑对于一个区间,它的消除一定是通过几个不同的区间一起消除,或者是最后左右端点合并进行消除。所以我们一定能重排操作序列,使得这个区间的最后一次操作在左右端点处,这样方便于我们设计状态。因为这道题左右端点其实是差不多等价的,所以我们就定义 为消完区间 之后的最大利润, 表示区间 中消完最后剩下一个颜色为 ,重量为 的史莱姆的最大利润,需要保证中间的过程中,最左侧的史莱姆没有被消掉。
最后一次的消除有两种情况,第一种是花钱加重量后消除,第二种是两个同颜色的撞在一起之后可以直接消除。我们先来看第一种。
我们有一个比较显然的转移:
的转移也较容易。首先有 。然后因为最左侧史莱姆没有消掉,所以有 。(为什么没有 :上面那个式子显然已经包含了这个东西)注意上述两个转移不能有边界上的合并颜色,下面的转移同样需要注意,后面就不赘述这一部分了。
接下来我们来转移第二种情况。采用分步转移的思想(因为再定义一个 ,然后枚举两个颜色相等点转移的复杂度至少有一个 ,无法通过),设 为合并完 之后,剩下的物品颜色为 ,重量为 。
所以我们显然有:。接下来转移 就大功告成了。而 其实和 差不多:
总时间复杂度 。
代码
#include<bits/stdc++.h>
using namespace std;
int n,k;
#define ll long long
ll p[21],w;
ll f[155][155],fl[155][155][11],fr[155][155][11],g[155][155][11];
void renew(ll &x,ll y){
if(x<y)x=y;
return;
}
int c[155],m[155];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k>>w;
for(int i=1;i<=n;i++)cin>>c[i];
for(int j=1;j<=n;j++)cin>>m[j];
for(int i=k;i<=2*k-2;i++)cin>>p[i];
for(int i=1;i<=n;i++){
for(int j=i;j<=n;j++){
f[i][j]=-1e18;
for(int o=1;o<=k;o++)fl[i][j][o]=fr[i][j][o]=g[i][j][o]=-1e18;
}
}
for(int i=1;i<=n;i++)f[i][i]=p[k]-w*(k-m[i]),fl[i][i][m[i]]=fr[i][i][m[i]]=0;
for(int i=2;i<=n;i++){
for(int l=1;l<=n-i+1;l++){
int r=l+i-1;
fl[l][r][m[l]]=f[l+1][r];
fr[l][r][m[r]]=f[l][r-1];
for(int t=l+1;t<=r;t++)if(c[t]==c[l])for(int o=m[l]+1;o<k;o++)renew(fl[l][r][o],f[l+1][t-1]+fl[t][r][o-m[l]]);
// for(int t=l;t<=r;t++)if(c[t]==c[r])for(int o=m[r]+1;o<k;o++)renew(fr[l][r][o],fr[l][t][o-m[r]]+f[t+1][r-1]);
for(int t=l;t<=r;t++)if(c[l-1]!=c[t]&&c[t]!=c[r+1])for(int o=1;o<k;o++)renew(f[l][r],f[l][t-1]+fl[t][r][o]+p[k]-w*(k-o));
for(int t=l;t<=r;t++)if(c[t]==c[r+1])for(int o=1;o<k;o++)renew(g[l][r][o],fl[t][r][o]+f[l][t-1]);
for(int t=l+1;t<=r;t++)if(c[t]!=c[l-1]&&c[t]!=c[r+1])
for(int o1=1;o1<k;o1++)for(int o2=1;o2<k;o2++)if(o1+o2>=k)renew(f[l][r],g[l][t-1][o1]+fl[t][r][o2]+p[o1+o2]);
}
}
cout<<f[1][n];
return 0;
}
背包 DP
背包 DP,顾名思义,即使用 DP 的思想解决把物品放到背包里的物品。想必大家对 01 背包,完全背包,多重背包,分组背包都掌握了。所以我们板题就不放了。
依赖性背包大多是树形背包,DAG 上的依赖背包作者不会,如果读者会的话可以私信作者。
有一些板题,我看大家好像没怎么做,这里还是浅浅说说吧。
一些板题
板题:P1064 [NOIP2006 提高组] 金明的预算方案
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 元钱就行”。今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
主件 附件 电脑 打印机,扫描仪 书柜 图书 书桌 台灯,文具 工作椅 无 如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有 个、 个或 个附件。每个附件对应一个主件,附件不再有从属于自己的附件。金明想买的东西很多,肯定会超过妈妈限定的 元。于是,他把每件物品规定了一个重要度,分为 等:用整数 表示,第 等最重要。他还从因特网上查到了每件物品的价格(都是 元的整数倍)。他希望在不超过 元的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 件物品的价格为 ,重要度为 ,共选中了 件物品,编号依次为 ,则所求的总和为:
。
总物品个数为 ,请你帮助金明设计一个满足要求的购物单。
对于全部的测试点,保证 ,,,,,答案不超过 。
题解
这题看样子像一个依赖性背包问题,但是因为只可能有两个附件,而且附件没有其他附件,所以其实可以对每个主件讨论选不选附件,选多少附件,情况数较少。
把一个主件的所有情况分为一组,对全局做一个分组背包即可。
时间复杂度为 。
对于大家来说过于简单,就不贴代码了。
习题,板题:P1941 [NOIP2014 提高组] 飞扬的小鸟
较为板子的题:P1417 烹调方案
一共有 件食材,每件食材有三个属性,, 和 ,如果在 时刻完成第 样食材则得到 的美味指数,用第 件食材做饭要花去 的时间。
众所周知,gw 的厨艺不怎么样,所以他需要你设计烹调方案使得在总花费时间小于等于 时美味指数最大。
,其他数字均小于 。
据说是泛化物品的一道题。随机大法好。
题解
这个题如果没有那个 的美味指数限制,那就是一个显然的 01 背包问题。但是因为结束时间改变会导致权值改变,所以显然不能把所有物品看做等价。
因为从时间上枚举会导致物品算重,所以还是只能使用类似于背包的方法加入物品。我们尝试对于两个物品在最优解中的顺序进行贪心。
使用 exchange arguments 思想,考虑我们把最优顺序的两个物品交换顺序,我们发现只会有这两个物品受到影响,设这两个物品为 号和 号, 号原来在前面,下面我们列出不等式:
我们发现,这个东西可以变成一个每个元素可以算出来的值的比较,所以我们可以直接对这个值进行排序以得到最优的顺序,其他的就交给 01 背包就行了。
代码
#include<bits/stdc++.h>
using namespace std;
int T,n,a[51],b[51],c[51];
long long dp[100005];
int id[51];
bool cmp(const int &x,const int &y){
return 1ll*c[x]*b[y]<1ll*b[x]*c[y];
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>T>>n;
for(int i=1;i<=n;i++)cin>>a[i],id[i]=i;
for(int i=1;i<=n;i++)cin>>b[i];
for(int i=1;i<=n;i++)cin>>c[i];
sort(id+1,id+n+1,cmp);
for(int i=1;i<=n;i++){
for(int j=T;j>=c[id[i]];j--){
dp[j]=max(dp[j],dp[j-c[id[i]]]+a[id[i]]-1ll*j*b[id[i]]);
}
}
long long ans=0;
for(int i=1;i<=T;i++)ans=max(ans,dp[i]);
cout<<ans;
return 0;
}
接下来就是不那么板的题了。
P2851 [USACO06DEC] The Fewest Coins G
农夫 John 想到镇上买些补给。为了高效地完成任务,他想使硬币的转手次数最少。即使他交付的硬 币数与找零得到的的硬币数最少。
John 想要买价值为 的东西。有 ()种货币参与流通,面值分别为 ()。John 有 个面值为 的硬币()。
我们假设店主有无限多的硬币, 并总按最优方案找零。注意无解输出
-1。。
题解
注意到其实这个题如果确定了背包容量的上界那就是一个多重背包和完全背包糅在一起的板子题,即先算一个每个物品个数为 的多重背包 ,再算一个完全背包 ,最后合并一下答案:。
问题就在确定 的最大值。考虑卖家的还的硬币的序列是 ,买家给的硬币的序列是 ,我们现在尽量找到 和 中可以抵消的部分。对于一个 ,如果 中的元素个数大于 ,我们把 定一个序不难发现前缀和序列中一定存在至少两个元素同余 。这样的话我们可以把 拆成两部分 和 ,其中 中元素和是 的倍数。我们可以把 中的元素换成 个 ,然后就可以和 中原来的 进行抵消。
但是抵消不一定是优的,所以我们还要继续探讨抵消的具体情况。
设卖家还的金币最少的形式为 ( 是集合,其内没有 这个元素),根据上面抵消的步骤,不难发现如果集合 中存在 个元素一定能把其中的某些元素化成 以达到更优,所以在最少的形式中 。
考虑假如说此时 中有一个元素个数 ,我们也可以将它变成 来减小 的大小,所以在最少的情况下,如果 , 中才可能有 这个元素,而 的话 。
再进一步,我们把 分成 和 两个集合,其中 的和刚过 ,为保证不会产生可以换成 的机会,我们必须保证 的大小小于 ,这样稍微经过一下放缩就可以得到 。
那么这道题就结束了,二进制分组或单调队列优化均能够通过。
可能证明不太严谨,如果读者有疑问可以提出。
代码
#include<bits/stdc++.h>
using namespace std;
int dp[24405],T,n;
int V[105],C[105];
int v[10005],w[10005],ocnt;
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>T;
for(int i=1;i<=n;i++)cin>>V[i];
for(int i=1;i<=n;i++){
cin>>C[i];
int now=0,num=C[i];
while(num>=(1<<now)){
v[++ocnt]=(1<<now)*V[i];
w[ocnt]=(1<<now);
num-=(1<<now);
now++;
}
if(num){
v[++ocnt]=num*V[i];
w[ocnt]=num;
}
}
memset(dp,0x3f,sizeof dp);
dp[0]=0;
for(int i=1;i<=ocnt;i++){
for(int j=T+14400;j>=v[i];j--){
dp[j]=min(dp[j],dp[j-v[i]]+w[i]);
}
}
for(int i=1;i<=n;i++){
for(int j=T+14400-V[i];j>=0;j--){
dp[j]=min(dp[j],dp[j+V[i]]+1);
}
}
if(dp[T]>=1e9)dp[T]=-1;
cout<<dp[T];
return 0;
}
P7606 [THUPC2021] 混乱邪恶
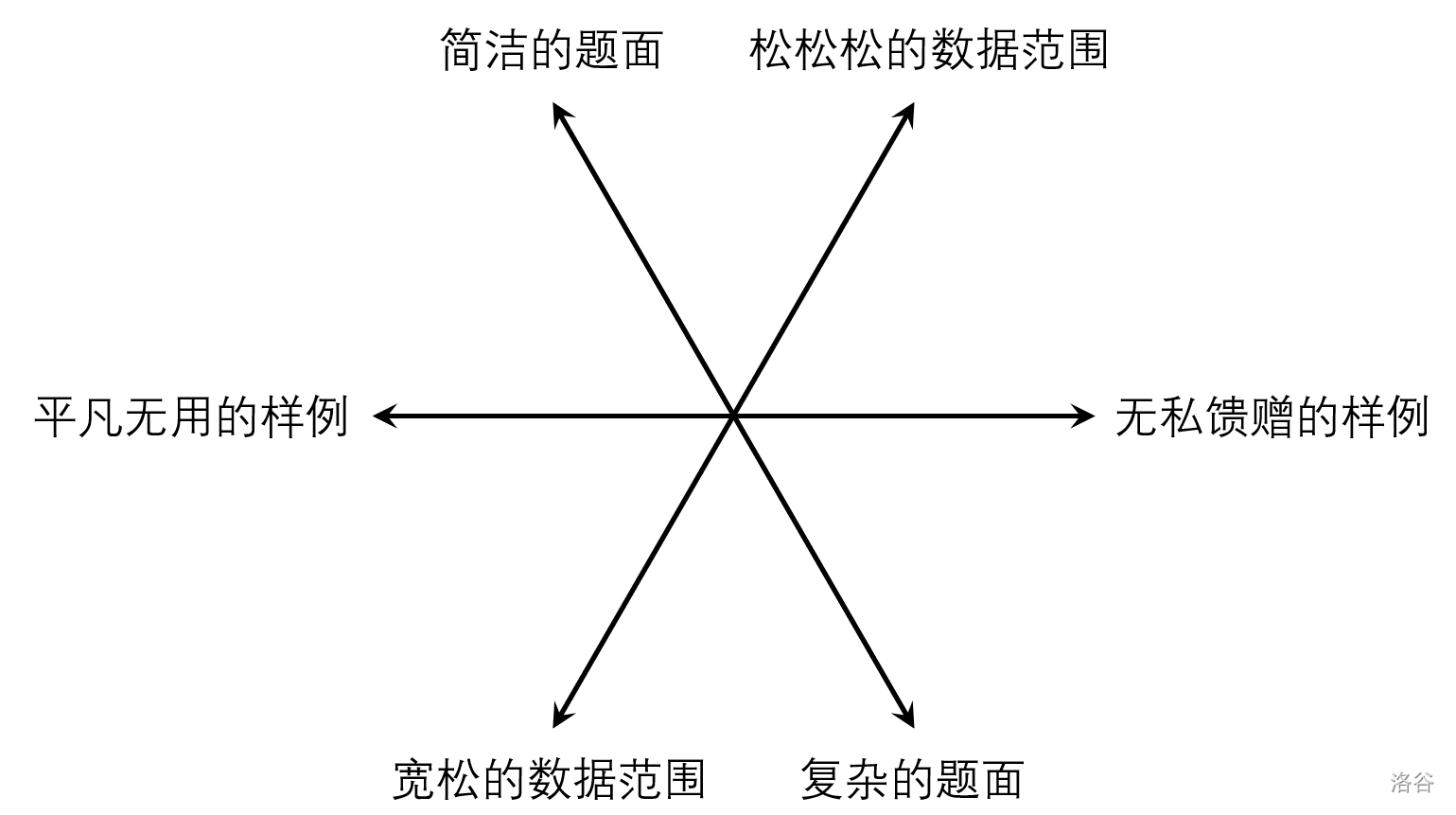
每个出题人都有一个守序指数 和善良指数 。对于一个 idea,从题面、样例或数据范围的角度,可以从 个方向中选择恰好一个作为这个 idea 对应的题目的特有风格,同时会在境界中沿着所选的箭头方向移动一步:
你现在一共有 个 idea,你知道你给每个 idea 设定某一个风格时你的 指数和 指数的变化。具体地,对于第 个idea有 个参数 :
如果选择“简洁的题面”,那么 变成 , 变成 ;
如果选择“平凡无用的样例”,那么 变成 , 变成 ;
如果选择“宽松的数据范围”,那么 变成 , 变成 ;
如果选择“复杂的题面”,那么 变成 , 变成 ;
如果选择“无私馈赠的样例”,那么 变成 , 变成 ;
如果选择“松松松的数据范围”,那么 变成 , 变成 。
这里所有的加法都在模 意义下进行。
进入混乱邪恶阵营的要求很苛刻,需要 恰好等于 且 恰好等于 。
你的 指数和 指数开始时都为 。请问是否存在一种设定风格的方式使得设定完全部 个 idea 的风格后你仍在境界中原来的位置,但是能够进入混乱邪恶阵营。
。所有其他输入数字均保证属于 。
Hint
注意到暴力做是 的,可以尝试通过某些手段降到 。
题解
首先把这个六个出边的东西变成一个坐标系类的东西方便转移。不难发现可以直接把斜率是 的直线直接掰成 轴,不难发现图会变成这样:

这样我们枚举坐标,枚举目前的 和 ,扫一遍所有物品,时间复杂度 。因为只需要记录可行性,所以可以用 bitset 优化,时间复杂度 。
有一个经典结论,随机游走 步之后距离原点的距离是 的,这里有一个一维的证明:stO uob。
而我们把物品随机打乱之后是等效的,相当于把答案序列在物品中的顺序打乱了,所以满足随机游走性质,我们只需要枚举 这个区间内的坐标值即可。这样时间复杂度为 。
如果是用 bitset 状压 一维,因为有一个取模,所以需要用循环位移,可能比较困难。可以状压 轴,这样用 int 就行了,而且转移也较为简单,复杂度为 ,以上两种做法均能通过。
如果枚举边界就是 的话可能过不了,可能需要多次提交。
代码
#include<bits/stdc++.h>
using namespace std;
int num[105][11][3];
unsigned int f[2][105][105][25];
int n,p,F,G;
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>p;
for(int i=1;i<=n;i++){
for(int j=1;j<=6;j++){
cin>>num[i][j][0]>>num[i][j][1];
num[i][j][0]%=p;
num[i][j][1]%=p;
}
}
shuffle(num+1,num+n+1,rnd);
cin>>F>>G;
F%=p;
G%=p;
int now=1,ed=0;
int sq=sqrt(n)+1;
f[0][0][0][sq+1]=1<<(sq+1);
//[1,sq+1,sq*2+1]
for(int i=1;i<=n;i++){
memset(f[now],0,sizeof f[now]);
for(int x=0;x<p;x++){
for(int y=0;y<p;y++){
for(int po=1;po<=sq*2+1;po++){
int gx=(x+num[i][1][0])%p,gy=(y+num[i][1][1])%p;
f[now][gx][gy][po]|=f[ed][x][y][po]<<1;
gx=(x+num[i][2][0])%p,gy=(y+num[i][2][1])%p;
f[now][gx][gy][po]|=f[ed][x][y][po+1];
gx=(x+num[i][3][0])%p,gy=(y+num[i][3][1])%p;
f[now][gx][gy][po]|=f[ed][x][y][po+1]>>1;
gx=(x+num[i][4][0])%p,gy=(y+num[i][4][1])%p;
f[now][gx][gy][po]|=f[ed][x][y][po]>>1;
gx=(x+num[i][5][0])%p,gy=(y+num[i][5][1])%p;
f[now][gx][gy][po]|=f[ed][x][y][po-1];
gx=(x+num[i][6][0])%p,gy=(y+num[i][6][1])%p;
f[now][gx][gy][po]|=f[ed][x][y][po-1]<<1;
}
}
}
swap(now,ed);
}
if(f[ed][F][G][sq+1]&(1<<(sq+1)))cout<<"Chaotic Evil\n";
else cout<<"Not a true problem setter\n";
return 0;
}
P9140 [THUPC 2023 初赛] 背包
本题中,你需要解决完全背包问题。
有 种物品,第 种物品单个体积为 、价值为 。
次询问,每次给出背包的容积 ,你需要选择若干个物品,每种物品可以选择任意多个(也可以不选),在选出物品的体积的和恰好为 的前提下最大化选出物品的价值的和。你需要给出这个最大的价值和,或报告不存在体积和恰好为 的方案。
为了体现你解决 NP-Hard 问题的能力, 会远大于 ,详见数据范围部分。
。
Hint
你应该发现了这个题是同余最长路了吧!SPFA 可能无法通过,考虑回归背包本质。
题解
首先我们把性价比最高的物品拉出来能选就选。我们最后可能剩下一些容量没选。我们考虑利用类似于同余最短路的处理办法来处理这个问题。
考虑我们连边 ,如果这里取模无效,那么边权一定是 ,但是溢出了一部分怎么办呢?考虑我们不是已经钦定了能选就选,所以我们溢出多少次就一定会扔掉多少个我们之前选的性价比最高的物品。整合一下,边权就是 。最后跑一遍最长路即可。此时每个节点代表的是当余数为当前数的时候为了填满容积 得到的额外最大价值。因为 ,而我们一定能在 的体积内凑出这个额外最大价值,所以这种做法是没有问题的。
SPFA 是可以的,最坏时间复杂度为 ,被卡了。
于是我们引入解决同余最短路类问题的利器:转圈 DP!
考虑回归本质,这就是一个完全背包。同样引入取模来减小值域,这里的转移就变成在同余系内转移。
我们观察这个转移,它形成了 个环,因为保证了把性价比最高的物品作为同余系,所以一定没有正环,所以每一个点的转移都不会超过转一圈。如何将环上的每一个点都转移到呢?转一圈好像只能完整转移到一个元素。那就转两圈!你会发现这样转移就能把所有元素转移到了。
每次枚举每个环转两圈转移,时间复杂度为 。
非常好写。虽然有些时候 SPFA 比这个跑得快,但是这个能保证复杂度,学了这个之后谁还写 SPFA 啊。
代码
#include<bits/stdc++.h>
using namespace std;
int n,q;
long long v[51],c[51],id;
long long f[100005],V;
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>q;
v[0]=1;
for(int i=1;i<=n;i++){
cin>>v[i]>>c[i];
if(1ll*c[i]*v[id]>1ll*c[id]*v[i])id=i;
}
for(int i=1;i<=v[id];i++)f[i]=-1e18;
for(int i=1;i<=n;i++){
if(v[i]==v[id])continue;
for(int k=0,lim=__gcd(v[i],v[id]);k<lim;k++){
for(int j=k,_=0;_<2;_+=(j==k)){
int nxt=(j+v[i])%v[id];
f[nxt]=max(f[nxt],f[j]+c[i]-1ll*(j+v[i])/v[id]*c[id]);
j=nxt;
}
}
}
while(q--){
cin>>V;
if(f[V%v[id]]>=-1e12)cout<<1ll*(V/v[id])*c[id]+f[V%v[id]]<<"\n";
else cout<<-1<<"\n";
}
return 0;
}
[ABC221G] Jumping sequence
有一个无限大的平面直角坐标系,初始时你在 处。给你一个长度为 的序列 ,你可以移动 步,每一步可以选择:
向上移动 距离,从 到
向下移动 距离,从 到
向右移动 距离,从 到
向左移动 距离,从 到
你想在 步结束后位于 位置,问是否存在这样的方案,如果存在需输出任意一种方案。
,。
Hint
现在总执行次数使得两维互相限制,就是当前 选了某一维之后就不能选另外一维,可以尝试把 变一下使得两维之间互不限制。
题解
考虑我们有 种操作,两个维度,我们对于每一维某一步的参数只需要考虑正负,这里就有一个 的关系,所以考虑我们把每个操作变到两个维度上,然后这两个维度的物品的加入不互相限制。
考虑我们构造一个 的坐标 ,接下来我们模拟一下四个操作:
- 第一个操作将 增加 ,此时 增加 , 减少 。
- 第二个操作将 减少 ,此时 减少 , 减少 。
- 第三个操作将 增加 ,此时 增加 , 增加 。
- 第四个操作将 减少 ,此时 减少 , 减少 。
你会发现对 和 的操作是可以任意组合的,所以 和 是不互相限制的。稍微转化一下变成 01 背包之后就很简单了。
注意到这个是可行性背包,所以显然可以使用 bitset 优化,时间复杂度 。可以通过,但是我们接下来讲的 做法才是重点。
我们重新审视这个问题,不难发现我们就是想要在一个序列里面选几个数看能不能凑出来一个 。如果我们先选一些元素使得靠近于 ,然后进行调整的话,我们理论上有机会可以把值域控制到 。
考虑我们先在序列选出前 个数,使得这 。这样我们可以设状态 表示我们动 内的元素选择情况是否可以凑出 ,但是这样状态是 的,死活也不可能比上面那个 bitset 的做法优。但是我们发现如果 ,那么 。所以我们可以把状态换成 表示动右段点为 的一个区间凑出 的最大的 。这样状态数是 的。
我们来看看我们能不能控制这个值域,假如最优解要删除一个左端点元素,但是目前删除之后就会到这个值域之外,此时一定会加入一个新的右端点元素,先加入直到删除不会超出值域再删除就能够控制。所以我们现在来考虑转移。
首先扩充右端点有两种情况,即选上右端点的数还是不选上右端点的数,有:
接下来我们来讨论左端点的情况,显然我们此时只能枚举左端点来转移:
但是这样复杂度就回去了,考虑使用一些均摊性质。发现对于小于 的 ,可以先转移到 上然后再通过上面的第一个转移转移过来。所以我们只需要枚举 中间的 转移。
这样均摊下来的复杂度是 的。
注意到这个东西其实是可以解决任何可行性 01 背包问题的,但是这个东西最大的问题就是只能处理单次询问。苹果好像有一个逆天的处理多次询问的办法,但是个人感觉没什么用。
代码
#include<bits/stdc++.h>
using namespace std;
int n,a,b,x,y;
int d[2005];
const int D=1800;
int g[2005][2*D+5];
int ans[2005][2*D+5];
int ans0[2005],ans1[2005];
int tran(int C,int p){
return p-C+D;
}
void renew(int id1,int id2,int x,int val){
if(g[id1][id2]<x)g[id1][id2]=x,ans[id1][id2]=val;
return;
}
char p0[2][2]={{'L','D'},{'U','R'}};
bool solve(int C,int *res){
int nowsum=0,pos=n+1;
for(int i=1;i<=n;i++){
if(nowsum+d[i]>C){pos=i;break;}
nowsum+=d[i];
}
for(int i=1;i<pos;i++)res[i]=1;
if(nowsum==C)return 1;
memset(g,0,sizeof g);
memset(ans,0,sizeof ans);
g[pos-1][tran(C,nowsum)]=pos;
int CD=max(0,C-D);
for(int i=pos;i<=n;i++){
for(int j=C+D;j>=CD;j--){
renew(i,tran(C,j),g[i-1][tran(C,j)],-1);
if(j-d[i]>=C-D)renew(i,tran(C,j),g[i-1][tran(C,j-d[i])],-2);
for(int l=max(g[i-1][tran(C,j)],1);l<g[i][tran(C,j)];l++)if(j-d[l]>=C-D)renew(i,tran(C,j-d[l]),l,l);
}
}
if(!g[n][tran(C,C)])return 0;
int i=n,j=tran(C,C);
while(ans[i][j]!=0){
if(ans[i][j]==-1)i--;
else if(ans[i][j]==-2){res[i]=1,j-=d[i];i--;}
else{
res[ans[i][j]]=0;
j+=d[ans[i][j]];
}
}
return 1;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>a>>b;
int sum=0;
for(int i=1;i<=n;i++)cin>>d[i],sum+=d[i];
x=a+b,y=a-b;
if(x>sum||y>sum)return cout<<"No\n",0;
x+=sum,y+=sum;
if(x<0||y<0||x&1||y&1)return cout<<"No\n",0;
x/=2,y/=2;
if(!solve(x,ans0)||!solve(y,ans1))return cout<<"No\n",0;
cout<<"Yes\n";
for(int i=1;i<=n;i++){
cout<<p0[ans0[i]][ans1[i]];
}
return 0;
}
习题:[ABC240G] Teleporting Takahashi。
[ARC096F] Sweet Alchemy
有 个物品和 个特殊材料,制作第 个物品需要 个特殊材料。给出一个整数 ,对于每个 给定 ,设在材料充足的情况下制作第 个物品的个数为 ,需满足 。最大化制作的物品数。
。
背包魔王。
Hint
背包看样子非常不可做,可能需要部分贪心来缩小其值域。
题解第一部分
这个题非常巧妙。
首先不要看错题了,作者当时以为这是一棵基环树森林,虽然做法类似,但是还是提醒一下大家。显然这个题连出来的依赖边组成一棵树。
树的话我们就可以做一个对 限制的树上差分,这样我们可以把每个子树当成一个物品,重量为子树权值和,权值为子树大小。除了根物品可以无限选之外,其他的物品只能选 个。
这样我们把问题转化成一个混合背包问题,但是重量值域 ,很大,普通的混合背包是不可行的。但是我们关注到此题的 ,代表着这 个物品的价值都 ,是很小的。因为重量无法规约变小,背包状态数已经爆完了,所以我们考虑先缩状态,一个较为简单的想法就是考虑根据价值 这个性质把状态转为价值。
于是我们设 为前 个物品总价值为 的时候需要的最小重量。但是 ,物品可能会被选 次,状态依然很大,但是这样我们可以顺着思路继续向下,考虑怎么去缩小物品可能被选的次数。
树几乎不能给我们权值上的一些信息,所以我们只能考虑背包之外的东西,考虑贪心。首先我们有一个对于背包而言经典的贪心假做法,即按照性价比 排序,然后能选的都选。在这道题中, 很小,这启示我们可以通过性价比来规约物品选择的次数。
首先我们不难发现,如果我们按性价比从大到小排序后选了 个物品 ,而 ,我们一定可以把这一部分物品替换成 个物品 ,因为这样价值不变,而重量变少(根据排序有 )。
所以我们可以发现一个非常重要的结论,具体是什么可以看题解的下一部分,这里作者相信读者此时已经能够做出此题了。最后再给一个提示:根据上面的分析与结论,我们进行一次每个物品至多选 次的背包就能解决问题。
题解第二部分
根据上面的分析,我们可以发现,答案序列中,对于排序后的序列下标 的物品, 和 的情况一定不能共存,否则进行一次上面的转换一定会更优。
那么我们有结论:对于排序后数组下标有关系 的物品,一定有 或 。
适当放宽一下限制,上面这个式子不太适用于规约,因为有 ,所以我们可以把限制写为 或 。
这个时候做法其实已经很明显了,观察到这样我们把除了根物品和一个中间物品之外的物品的选择次数全部规约到了 的一个范围内,我们可以画出最优方案选择次数的一个示意图:
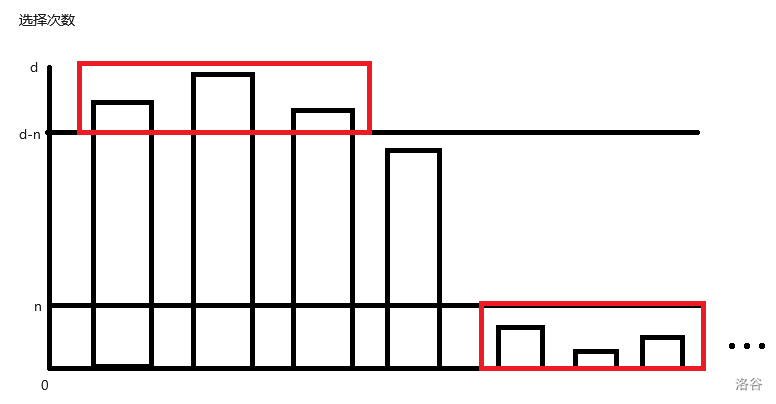
我们可以把红框部分背包处理掉,每种物品最多 个,所以值域大小只用开到 。多重背包或混合背包的总复杂度是 或 ,均能通过。
剩下的部分我们发现就是直接按贪心顺序来整的,直接枚举背包状态进行贪心计算答案即可。这一部分复杂度 。注意到反正要贪心,所以上面的背包中其实可以不用加入根物品,也就是可以只用多重背包做。
贪心时特判根物品无数量限制,其余物品数量限制为 ,总时间复杂度为 或 ,轻松跑过。
代码
#include<bits/stdc++.h>
using namespace std;
int n,x,d;
int m[51],y;
vector<int> E[51];
int siz[51];//v
#define ll long long
#define int long long
ll nw[51];//w
void dfs(int now,int f){
siz[now]=1;
nw[now]=m[now];
for(auto p:E[now]){
if(p^f){
dfs(p,now);
siz[now]+=siz[p];
nw[now]+=nw[p];
}
}
return;
}
ll f[125005];
int lim;//n*n*n
void ins(int v,int w){
for(int i=lim;i>=v;i--)f[i]=min(f[i-v]+w,f[i]);
return;
}
void _2(int v,int w,int c){
for(int i=0;(1<<i)<=c;i++){
ins((1<<i)*v,(1<<i)*w);
c-=(1<<i);
}
if(c)ins(c*v,c*w);
return;
}
struct info{
int v;
ll w;
int id;
inline bool operator <(const info &z)const{return 1ll*v*z.w>w*z.v;}
}P[51];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>x>>d;
lim=n*n*n;
for(int i=1;i<=lim;i++)f[i]=1e18;
cin>>m[1];
for(int i=2;i<=n;i++){
cin>>m[i]>>y;
E[i].push_back(y);
E[y].push_back(i);
}
dfs(1,0);
for(int i=2;i<=n;i++)_2(siz[i],nw[i],min(d,n));
for(int i=1;i<=n;i++)P[i]={siz[i],nw[i],i};
sort(P+1,P+n+1);
int ans=0;
for(int i=0;i<=lim;i++){
if(f[i]>x)continue;
int w=x-f[i],v=i,tp;
for(int j=1;j<=n;j++){
if(P[j].id==1){
v+=w/P[j].w*P[j].v;
w%=P[j].w;
}else{
tp=min(max(0ll,(ll)d-n),w/P[j].w);
v+=tp*P[j].v;
w-=tp*P[j].w;
}
}
ans=max(ans,v);
}
cout<<ans<<"\n";
return 0;
}
高兴吧!背包回归了一道题,但是不是新魔王。经过苹果的讲解感觉这道题非常简单。
gym101064L The Knapsack problem
ACM 领先学术界!
完全背包的题意。
。 是重量, 是容量。
大概没学过是想不出来的,直接上题解。
题解
因为是完全背包,所以我们可以直接 。
如果一个区间的 值满足任意转移一定会经过这个区间,那么从这个区间转移过来就一定正确。不难发现该区间长为 ,所以每次我们砍半转移,对于计算 ,可以计算 ,不难发现每次拓展出的区间长一定不超过 ,那么一共只有 个点需要被计算,总时间复杂度为 。
如果 ,不难发现每次只需要对于相同的 ,只选取最大的 ,所以我们一定能将物品种数降为 级别。所以为了方便实现,我们可以先预处理出 为值域上界的背包。
代码是简单的。注意到 cc_hash_table 比 gp_hash_table 快 50 倍。
代码
v#include<bits/stdc++.h>
using namespace std;
#include<ext/pb_ds/hash_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/exception.hpp>
using namespace __gnu_pbds;
#define ll long long
cc_hash_table<int,ll> mp;
ll dp[1005];
int w[1005],v[1005],n;
int mw;
ll dfs(int S){
if(S<=mw+1)return dp[S];
if(mp.find(S)!=mp.end())return mp[S];
ll res=0;
for(int i=S/2-mw/2;i<=S/2;i++)res=max(dfs(i)+dfs(S-i),res);
return mp[S]=res;
}
int S;
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>S;
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i];
mw=max(mw,w[i]);
}
for(int i=1;i<=n;i++)for(int j=w[i];j<=mw+1;j++)dp[j]=max(dp[j-w[i]]+v[i],dp[j]);
cout<<dfs(S);
return 0;
}
状压 DP
当某个状态的情况数很少,但是有多个这样的状态,我们可以用一个数把这些状态的信息压缩下来。我们称这类 DP 叫做状压 DP。
直接上例题。
P2704 [NOI2001] 炮兵阵地
司令部的将军们打算在 的网格地图上部署他们的炮兵部队。
一个 的地图由 行 列组成,地图的每一格可能是山地(用 表示),也可能是平原(用 表示),如下图。
在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。
图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
。
大家好像都是状压两行?但是把格子搞成影响 列的时候再状压 行好像就不太优秀了。这种情况下,在不使用轮廓线 DP 的前提下,我们仍然有低于 的状压做法。
题解
直接压三进制/qiang。
考虑设一个三进制数为状态,其中 代表可选, 代表下一行可选这个位置, 代表下下行才能选这个位置。
对于一个三进制数,把它的 揪出来组成一个二进制数,其他 都变成二进制数中的 ,转移相当于枚举这个二进制数的超集。考虑一下复杂度,列出式子:
显然单次转移复杂度至少是 的,这里可以通过一大堆预处理把单次转移复杂度维持在 而不乘 ,具体可以参考代码。总时间复杂度为 ,有点卡。
考虑扩展,当问题变为影响 行的格子不能被选的时候,我们变成状压四进制,其余不变,不难发现单次转移复杂度式子变为:
作者不太会证这个东西的复杂度,但是至少我们能轻易看出其低于 ,高于 ,算是比较优秀了。
代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int zt[105];
char c;
int f[2][60005];
int _3[13];//0->good 1-> 1left 2-> 2left
int r2;
int _3to2(int num){
r2=0;
for(int i=m-1;i>=0;i--){
if(num<_3[i])r2|=(1<<i);
else num%=_3[i];
}
return r2;
}
inline int nxt(int p,const int &num){
for(int i=m-1;i>=0;i--)if((1<<i)&num)p+=_3[i]<<1;
return p;
}
void print3(int num){
for(int i=m-1;i>=0;i--){
cerr<<num/_3[i];
num%=_3[i];
}
return;
}
int _2[2004],p2[2004];
vector<int> V[2004];
inline int max(int a,int b){return a<b?b:a;}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
_3[0]=1;
for(int i=1;i<=10;i++)_3[i]=_3[i-1]*3;
for(int i=1;i<=n;i++){
for(int j=0;j<m;j++){
cin>>c;
if(c=='P')zt[i]|=1;
zt[i]<<=1;
}
zt[i]>>=1;
}
for(int i=0;i<(1<<m);i++)p2[i]=nxt(0,i);
for(int i=0;i<(1<<m);i++)_2[i]=__builtin_popcount(i);
for(int i=0;i<(1<<m);i++){
int lst=-4,flg=0;
for(int k=i;k;k=(k-1)&i){
lst=-4;
flg=0;
for(int o=0;o<m;o++)if(k&(1<<o)){if(o-lst<3){flg=1;break;}else lst=o;}
if(flg)continue;
V[i].push_back(k);
}
}
int now=1,ed=0;
for(int i=1;i<=n;i++){
memset(f[now],0,sizeof f[now]);
int p,lst;
for(int j=0;j<_3[m];j++){
p=_3to2(j)&zt[i];
int tj=0,ttj=j;
for(int k=m-1;k>=0;k--){
if(ttj>=(_3[k]<<1))tj+=_3[k];
ttj%=_3[k];
}
for(auto k:V[p]){
lst=tj+p2[k];
f[now][lst]=max(f[now][lst],f[ed][j]+_2[k]);
}
f[now][tj]=max(f[now][tj],f[ed][j]);
}
swap(ed,now);
}
int ans=0;
for(int i=0;i<_3[m];i++)ans=max(f[ed][i],ans);
cout<<ans<<"\n";
return 0;
}
然后 NIT 说这题每行状态只有 ,我的评价是,勾矢题,下次请出一个横着不互相影响的题。
P2473 [SCOI2008] 奖励关
你正在玩你最喜欢的电子游戏,并且刚刚进入一个奖励关。在这个奖励关里,系统将依次随机抛出 次宝物,每次你都可以选择吃或者不吃(必须在抛出下一个宝物之前做出选择,且现在决定不吃的宝物以后也不能再吃)。
宝物一共有 种,系统每次抛出这 种宝物的概率都相同且相互独立。也就是说,即使前 次系统都抛出宝物 (这种情况是有可能出现的,尽管概率非常小),第 次抛出各个宝物的概率依然均为 。
获取第 种宝物将得到 分,但并不是每种宝物都是可以随意获取的。第 种宝物有一个前提宝物集合 。只有当 中所有宝物都至少吃过一次,才能吃第 种宝物(如果系统抛出了一个目前不能吃的宝物,相当于白白的损失了一次机会)。注意, 可以是负数,但如果它是很多高分宝物的前提,损失短期利益而吃掉这个负分宝物将获得更大的长期利益。
假设你采取最优策略,平均情况你一共能在奖励关得到多少分值?
,,。
前两个题都比较简单,放在这里给大家先练练手。
题解
由于是期望,还要最优策略,那就是铁定的倒着 DP 了。
我们把 之前是否选过物品 i 压成一个状态,转移就只需要比较选物品 所到达的状态还是不选到达的状态优就行了。通过预处理,复杂度可以做到 。
代码
#include<bits/stdc++.h>
using namespace std;
int k,n;
long double f[2][(1<<15)];
vector<int> v[1<<15];
int sc[16];
vector<int> zt;
vector<int> de[16];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>k>>n;
int tp;
for(int i=1;i<=n;i++){
cin>>sc[i];
cin>>tp;
for(int j=1;tp;j++){
de[i].push_back(tp);
cin>>tp;
}
}
bool flg=0;
for(int i=0;i<(1<<n);i++){
for(int j=0;j<n;j++){
flg=0;
for(auto p:de[j+1])if(!((1<<(p-1))&i)){flg=1;break;}
if(!flg)v[i].push_back(j+1);
}
}
for(int i=0;i<(1<<n);i++){
flg=0;
for(int j=0;j<n;j++){
if((1<<j)&i)for(auto p:de[j+1])if(!((1<<(p-1))&i)){flg=1;break;}
}
if(!flg)zt.push_back(i);
}
int now=1,ed=0;
for(int i=k;i>=1;i--){
memset(f[now],0,sizeof f[now]);
for(auto j:zt){
for(auto p:v[j])f[now][j]+=(1.0/n)*max(f[ed][j],f[ed][j|(1<<(p-1))]+sc[p]);
f[now][j]+=(1.0*(n-v[j].size())/n)*f[ed][j];
}
swap(now,ed);
}
cout<<fixed<<setprecision(6)<<f[ed][0]<<"\n";
return 0;
}
P3226 [HNOI2012] 集合选数
《集合论与图论》这门课程有一道作业题,要求同学们求出 的所有满足以下条件的子集:若 在该子集中,则 和 不能在该子集中。
同学们不喜欢这种具有枚举性质的题目,于是把它变成了以下问题:对于任意一个正整数 ,如何求出 的满足上述约束条件的子集的个数(只需输出对 取模的结果),现在这个问题就交给你了。
Hint
这个题是一个独立集问题。回想我们之前做的一些独立集问题,我们可以考虑把这道题的独立集问题规约到比较板的独立集问题来做。
题解
想想我们已经会了哪些独立集问题,我们可以通过树形 DP 来做树上的独立集问题,我们可以通过状压 DP 来做矩阵的独立集问题,而我们已知序列上的独立集计数问题就是斐波那契数列。这道题一个数 可能会被四个数规约,即 ,这让我们想到了矩阵一个元素相邻有四个元素,考虑我们把上面那个问题转换成矩阵。
我们可以构造一个矩阵,竖着每个数是上一行对应数的两倍,横着每个数是上一列对应数的三倍,我们发现原题问题变成了在这个矩阵上求独立集计数。
因为有不整除于 或 的数,我们对 以内的每个这样的数都建立出矩阵求解。状压横着一列就能做到一个比较优秀的复杂度,具体作者不会证明。
代码
#include<bits/stdc++.h>
using namespace std;
int n;
int mat[21];
vector<int> v[1<<12];
int f[2][1<<12];
int num[21][12];
const int mod=1e9+1;
int solve(int len,int L){
for(int i=0;i<(1<<len);i++)f[0][i]=0;
f[0][0]=1;
int now=1,ed=0;
for(int i=1;i<=L;i++){
for(int j=0;j<(1<<len);j++)f[now][j]=0;
for(int j=0;j<(1<<len);j++)for(auto p:v[(((1<<len)-1)^j)&mat[i]])(f[now][p]+=f[ed][j])%=mod;
swap(now,ed);
}
int ans=0;
for(int i=0;i<(1<<len);i++)ans=(ans+f[ed][i])%mod;
return ans;
}
bool vis[100005];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=0;i<(1<<12);i++){
for(int k=i;k;k=(k-1)&i)if(!(k&(k<<1)))v[i].push_back(k);
v[i].push_back(0);
}
long long ans=1;
for(int i=1;i<=n;i++){
if(!vis[i]){
int H=0,W=0;
for(int o=1,oo=i;oo<=n;oo*=2,o++){
for(int k=oo,j=1;k<=n;k*=3,j++){
num[o][j]=k;
vis[k]=1;
H=max(H,o),W=max(W,j);
}
}
for(int j=1;j<=H;j++){
mat[j]=0;
for(int k=1;k<=W;k++){
if(num[j][k]<=n&&num[j][k]>0)mat[j]|=(1<<(k-1));
}
}
ans=ans*solve(W,H)%mod;
for(int j=1;j<=H;j++){
for(int k=1;k<=W;k++){
num[j][k]=0;
}
}
}
}
cout<<ans;
return 0;
}
CF1149D Abandoning Roads
一张 个点 条边的无向图,只有 两种边权(),对于每个 ,求图中所有的最小生成树中,从 到 距离的最小值。
。
Hint
注意到只有两种边权,根据 Kruskal 或者最小生成树的性质,我们发现最小生成树是由小边权边组成的每个连通块内的一棵树和将小边权联通块缩点之后的一棵重边树。这样我们就方便设计状态了。
题解
以下设小边权边为轻边,大边权边为重边。
首先我们只连轻边,我们会得到一些连通块,根据最小生成树的性质,最小生成树中一定有一个部分是这些连通块的生成树。
然后我们将连通块缩点,只剩下重边,我们仍发现最小生成树一定有一个部分是剩下的图的生成树。
既然是生成树,正常跑最短路时可能会出现重边环,那是一定不行的。所以我们设计状态跑最短路来规避这个情况。设 表示当前 集合的连通块已经被走过时, 的最短路长度。容易发现可以类似最短路转移。时间复杂度 或 。
但是再仔细观察可以发现,有一些连通块是没有必要去规避这种情况的,其本来正常最短路就不会出现重边环。我们发现大小小于等于 的连通块就不会,因为在最坏情况下最远两点距离为 ,小于重边环最小长度 ,所以我们只需要记录大小 的连通块有没有走过,时间复杂度变为 或 。
前者是开两个队列 BFS 的复杂度,后面则是直接 Dijkstra 的复杂度,两者均可通过。
代码
#include<bits/stdc++.h>
using namespace std;
int n,m,a,b,x,y,z;
int dis[71][(1<<18)];
struct line{int to,w;};
vector<line> E[71],G[71];
bool vis[71];
int ltid[71],siz[71],lcnt;
int _4id[71],_4cnt;
int dfs(int now){
int res=1;
ltid[now]=lcnt;
vis[now]=1;
for(auto p:G[now])if(!vis[p.to])res+=dfs(p.to);
return res;
}
struct info{int S,u;};
queue<info> q1,q2;
info gres;
inline info getnxt(){
if(q1.empty()){gres=q2.front();q2.pop();}
else if(q2.empty()){gres=q1.front();q1.pop();}
else if(dis[q1.front().u][q1.front().S]>dis[q2.front().u][q2.front().S]){gres=q2.front();q2.pop();}
else {gres=q1.front();q1.pop();}
return gres;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m>>a>>b;
memset(dis,0x3f,sizeof dis);
for(int i=1;i<=m;i++){
cin>>x>>y>>z;
E[x].push_back((line){y,z});
E[y].push_back((line){x,z});
if(z==a){
G[x].push_back((line){y,z});
G[y].push_back((line){x,z});
}
}
for(int i=1;i<=n;i++)if(!vis[i]){lcnt++;siz[lcnt]=dfs(i);}
for(int i=1;i<=lcnt;i++)if(siz[i]>=4)_4id[i]=++_4cnt;
dis[1][0]=0;
q1.push((info){0,1});
int nxt;
while(!q1.empty()||!q2.empty()){
auto v=getnxt();
for(auto p:E[v.u]){
if(p.w==a){if(dis[p.to][v.S]>dis[v.u][v.S]+a)dis[p.to][v.S]=dis[v.u][v.S]+a,q1.push((info){v.S,p.to});}
else{
if(ltid[p.to]==ltid[v.u])continue;
if(_4id[ltid[p.to]]&&v.S&(1<<(_4id[ltid[p.to]]-1)))continue;
if(_4id[ltid[v.u]]){
nxt=v.S|(1<<(_4id[ltid[v.u]]-1));
if(dis[p.to][nxt]>dis[v.u][v.S]+b)dis[p.to][nxt]=dis[v.u][v.S]+b,q2.push((info){nxt,p.to});
}else if(dis[p.to][v.S]>dis[v.u][v.S]+b)dis[p.to][v.S]=dis[v.u][v.S]+b,q2.push((info){v.S,p.to});
}
}
}
for(int i=1;i<=n;i++)cout<<*min_element(dis[i],dis[i]+(1<<_4cnt))<<" ";
return 0;
}
[AGC012E] Camel and Oases
给定 个绿洲,第 个绿洲的坐标为 ,保证 。
现在有一个人在沙漠中进行旅行,他初始的背包的水容积为 升,同时他初始拥有 升水 ,每次到达一个绿洲时,他拥有的水的量将自动重置为容积上限(可以使用多次)。他现在可以选择两个操作来进行旅行:
走路,行走距离为 时,需要消耗 升水。清注意,任意时刻你拥有的水的数量不能为负数。
跳跃,令 为你当前拥有的水量,若 ,则你可以跳跃至任意一个绿洲,然后重置容积上界和所拥有的水量为 (向下取整)。
对于每一个 满足 ,你需要求解,当你在第 个绿洲作为起点时,你能否依次遍历其他所有绿洲。如果可以,输出
Possible,否则输出Impossible。。
这道题是评分上的状压魔王。
Hint
注意到我们跳一次会减半上限,我们可以把每次跳之后的情况预处理出来,然后剩下的问题就好做了。
题解
注意到如果我们有 升水的上限,那么我们一定可以把整个序列分割成几个区间,每个区间内的所有点都是互通的。我们可以预处理所有 层中每个点对应的区间的左端点和右端点,时间复杂度为 。
然后你发现这样我们就成功把问题转化成,每层选一个线段,每次钦定第一层选的是哪些线段,问你这些线段能不能覆盖所有整点。这样我们就能状压 DP 了,因为一共才 层。因为最后要钦定第一层选什么,所以我们目前可以不用加入第一层的线段,设 为选了 集合的层的线段,能覆盖 的最大的 。 是类似的,只不过是能覆盖 的最小的 。转移是简单的,设刚刚我们预处理左右端点数组为 ,有:
最后对于每一个第一层的线段都枚举集合判断 和 能否包含即可。注意到第一层线段个数如果大于 个还是无解,所以这一部分复杂度是 的。
总时间复杂度 。
记得把数组开够。
代码
#include<bits/stdc++.h>
using namespace std;
const int M=2e5+5,M2=(1<<19);
int n,V;
int x[M],ml[M2],mr[M2];
int L[20][M],R[20][M];
int ans[M],L1[M];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>V;
for(int i=1;i<=n;i++)cin>>x[i];
x[n+1]=1e9+V+1;
int li,cnt=0,lst;
for(int lim=(V<<1);lim;lim>>=1){
li=lim>>1;
cnt++;
lst=1;
for(int j=2;j<=n+1;j++){
if(x[j]-x[j-1]>li){
for(int k=lst;k<j;k++)L[cnt][k]=lst,R[cnt][k]=j-1;
assert(j-lst==1||li!=0);
lst=j;
}
}
R[cnt][n+1]=n;
L[cnt][0]=1;
}
fill(mr,mr+(1<<(cnt-1)),n+1);
for(int i=1;i<(1<<(cnt-1));i++){
for(int j=2;j<=cnt;j++){
if(i&(1<<(j-2))){
ml[i]=max(ml[i],R[j][ml[i^(1<<(j-2))]+1]);
mr[i]=min(mr[i],L[j][mr[i^(1<<(j-2))]-1]);
}
}
}
int cnt1=0;
lst=0;
for(int i=1;i<=n;i++)if(L[1][i]!=lst){cnt1++,lst=L[1][i];L1[cnt1]=lst;}
if(cnt1>cnt){
for(int i=1;i<=n;i++)cout<<"Impossible\n";
return 0;
}
for(int i=1;i<=cnt1;i++){
for(int j=0;j<(1<<(cnt-1));j++){
if(ml[j]+1>=L1[i]&&mr[((1<<(cnt-1))-1)^j]-1<=R[1][L1[i]]){ans[L1[i]]=1;break;}
}
}
for(int i=1;i<=n;i++)cout<<(ans[L[1][i]]?"Possible":"Impossible")<<'\n';
return 0;
}
数位 DP
数位 DP,顾名思义,就是以数位为状态的一种 DP 方式。在删改该部分题目前这一部分的题量达到了 题(
CF1073E Segment Sum
注:该题为选做题。
给定 ,求 之间的各数位上包含的不同数字不超过 个的所有数的和。答案对 取模。
保证 。
一上来就扔一道选做题是不是很吓人啊(
这道题比较板,认为自己已经掌握的读者可以跳过此题。
题解
状压已经选了什么,设 为后 位用了 集合的数,有没有超过原数的数的和和个数。注意前导 。
需要注意加入枚举到的位的贡献。
时间复杂度 。
代码
#include<bits/stdc++.h>
using namespace std;
#define popcount(x) __builtin_popcount(x)
#define int long long
int f[21][2][1<<10],g[21][2][1<<10],_10[21];
bool vis[21][2][1<<10];
int t[21],ans;
const int mod=998244353;
inline int add(int &s1,int &s2,pair<int,int> P){
s1=(s1+P.first)%mod;
s2=(s2+P.second)%mod;
return P.first;
}
pair<int,int> dfs(int pos,bool lim,int S,bool cp=0){
if(popcount(S)>pos)return make_pair(0,0);
if(!pos)return make_pair(1,0);
if(!popcount(S))return make_pair(0,0);
if(!cp&&vis[pos][lim][S])return make_pair(f[pos][lim][S],g[pos][lim][S]);
vis[pos][lim][S]=1;
int tp=lim?t[pos]:9,res=0,res2=0,tmp;
for(int i=cp;i<=tp;i++){
tmp=0;
if(!(S&(1<<i)))continue;
tmp=(tmp+add(res,res2,dfs(pos-1,lim&(i==tp),S^(1<<i))))%mod;
tmp=(tmp+add(res,res2,dfs(pos-1,lim&(i==tp),S)))%mod;
res2=(res2+1ll*tmp*i%mod*_10[pos-1]%mod)%mod;
}
return make_pair(f[pos][lim][S]=res,g[pos][lim][S]=res2);
}
int l,r,k;
int ask(int num){
memset(f,0,sizeof f),memset(g,0,sizeof g);
memset(vis,0,sizeof vis);
int cnt=0;
while(num){t[++cnt]=num%10;num/=10;}
int res=0;
for(int i=cnt;i>=1;i--)for(int j=0;j<(1<<10);j++)if(popcount(j)<=k)res=(res+dfs(i,(i==cnt),j,1).second)%mod;
return res;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
_10[0]=1;
for(int i=1;i<=18;i++)_10[i]=_10[i-1]*10%mod;
cin>>l>>r>>k;
cout<<(ask(r)-ask(l-1)+mod)%mod;
return 0;
}
P2481 [SDOI2010] 代码拍卖会
给定数字位数 和模数 ,求位数为 ,数字只有 ,并且数字升序排列的数模 等于 的个数。答案模 。
。
Hint
注意到数字升序排列,我们其实可以把每个这样的数拆成最多 个后缀全为 ,其余位为 的数字相加。
题解
把每个数字拆开,拆成最多 个后缀全为 ,其余位全为 的数字相加。因为位数固定为 ,所以我们一定会先选一个后缀 长度为 的数。
将剩下的最多 次选择拉出来 DP。设 为目前选的数模 余 ,选了 个数的方案数。这里我们把所有后缀 数扔进一个下标为 的桶 里计数。计数可以使用循环节性质。
然后我们枚举每一个桶,显然有:
其中这个组合数是从 中选出 个可以相同的元素的方案数,使用插板法易得。因为 ,所以在计算这个组合数的时候可以暴力计算。
DP 初始值就是先加入后缀 长度为 的数。时间复杂度 ,其中 。
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll n,p;
ll c[501];
ll vis[501];
ll _[11];
const int mod=999911659;
ll ksm(ll a,ll b){
if(!b)return 1;
return (b&1?a:1)*ksm(a*a%mod,b/2)%mod;
}
inline ll C(ll a,ll b){
if(!b)return 1;
if(a<b)return 0;
ll res=1;
for(int i=1;i<=b;i++)res=res*_[i]%mod;
for(ll i=a-b+1;i<=a;i++)res=res*(i%mod)%mod;
return res;
}
ll f[501][11][501];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
for(int i=1;i<=10;i++)_[i]=ksm(i,mod-2);
cin>>n>>p;
ll tmp=1%p,ccnt=0;
while(!vis[tmp]){
vis[tmp]=++ccnt;
tmp=(tmp*10+1)%p;
}
ll st=vis[tmp],len=ccnt-vis[tmp]+1;
for(ll i=1,j=1;i<min(st,n+1);i++,j=(j*10+1)%p)c[j]++;
if(n>=st){
ll cnt=(n-st+1)/len,lft=(n-st+1)%len;
ll k=tmp%p;
cnt%=mod;
do{
c[k]+=cnt;
k=(k*10+1)%p;
}while(k!=tmp);
ll i,j;
for(i=1,j=tmp;i<lft;i++,j=(j*10+1)%p)c[j]++;
if(lft){f[0][0][j]=1,c[j]++;}
else{
lft=max(1ll,len-1);
for(ll i=1,j=tmp;i<=lft;i++,j=(j*10+1)%p)if(i==lft)f[0][0][j]=1;
}
}else for(ll i=1,j=1;i<=n;i++,j=(j*10+1)%p)if(i==n)f[0][0][j]=1;
for(int i=1;i<=p;i++){
for(int s=0;s<=8;s++){
for(int j=0;j<p;j++){
for(int t=0;t<=8;t++){
if(s+t<=8){
(f[i][s+t][(j+(i-1)*t)%p]+=1ll*f[i-1][s][j]*C(c[i-1]+t-1,t)%mod)%=mod;
}
}
}
}
}
ll ans=0;
for(int i=0;i<=8;i++)ans=(ans+f[p][i][0])%mod;
return cout<<ans,0;
}
P3286 [SCOI2014] 方伯伯的商场之旅
方伯伯有一天去参加一个商场举办的游戏。商场派了一些工作人员排成一行。每个人面前有几堆石子。
说来也巧,位置在 的人面前的第 堆的石子的数量,刚好是 写成 进制后的第 位。现在方伯伯要玩一个游戏,商场会给方伯伯两个整数 。
方伯伯要把位置在 中的每个人的石子都合并成一堆石子。每次操作,他可以选择一个人面前的两堆石子,将其中的一堆中的某些石子移动到另一堆,代价是移动的石子数量 移动的距离。
商场承诺,方伯伯只要完成任务,就给他一些椰子,代价越小,给他的椰子越多。所以方伯伯很着急,想请你告诉他最少的代价是多少。例如: 进制下的位置在 的人,合并石子的最少代价为:即把所有的石子都合并在第三堆。
。
Hint
注意到移动的位置对应的答案是单峰的,所以我们可以计算最大值然后对每个位置注意计算减量,这样我们仍可以计算得到正确的代价。
题解
注意到移动终点对应的答案是单峰的,所以我们对于一个数,我们没有必要去用某些性质去找到最优点,我们可以把最右边的数当做移动终点,然后把这个终点一步步往前移直到答案变化不再为负。
放到全局,我们可以先做一个把最右边的数当成移动终点的数位 DP,然后再做一个一步步向前移,只计算负增量的数位 DP。只需记录一下目前的增量或者答案是多少即可,而这个东西理论不会很大。
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll l,r;
int k,t[71];
ll f[71][70110][2];
bool vis[71][7101][2];
void init(){memset(f,0,sizeof f),memset(vis,0,sizeof vis);}
ll dfs(int pos,int sum,bool lim,int to){
if(sum<0)return 0;
if(!pos)return sum;
if(vis[pos][sum][lim])return f[pos][sum][lim];
vis[pos][sum][lim]=1;
int tp=lim?t[pos]:k-1;ll res=0;
for(int i=0;i<=tp;i++){
if(to==1)res+=dfs(pos-1,sum+(pos-1)*i,lim&(i==tp),to);
else res+=dfs(pos-1,(pos>=to?i:-i)+sum,lim&(i==tp),to);
}
return f[pos][sum][lim]=res;
}
ll ask(ll num){
int cnt=0;
ll ans=0;
while(num){t[++cnt]=num%k;num/=k;}
init();
ans=dfs(cnt,0,1,1);
for(int i=2;i<=cnt;i++)init(),ans-=dfs(cnt,0,1,i);
return ans;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>l>>r>>k;
cout<<ask(r)-ask(l-1);
return 0;
}
下面两道题的实现均没有使用记忆化搜索。
CF908G New Year and Original Order
给 ,问 到 中每个数在各数位排序后得到的数的和。答案模 。
Hint
排序这个操作后的局面和刚刚的 P2481 很类似,但是对于一个这样的局面计数是困难的。考虑拆掉整个局面的贡献。
题解
考虑排序后,我们发现每个数一定在一个连续段上。我们可以把所有局面的贡献拆成所有局面中,每个数的贡献。这样我们可以枚举加入的数字 DP。
我们从小数位到大数位 DP(为了统计方便),钦定一个目前正在被计算贡献的数 。考虑加入数对其的影响。
假如说加入比 小的数,那么它一定被排到了前面;如果加入 ,那么它会被计算入贡献,并且之前的 的贡献会乘 ;如果加入比 大的数,那么它一定会排到 的后面,使 的贡献乘 。
所以我们设 为所有情况下,加入了后 位,是否顶到上界,数 的所有贡献。 位所有情况下,加入了后 位,是否顶到上界,在此情况下再加入一个数 ,新加入的 的所有贡献。这样我们就能 DP 了。
设选的数为 ,如果 ,有:
若 ,有:
最后,若 ,有:
对于每个数都要求的答案,总时间复杂度为 ,其中 。
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
char s[701];
int n,t[701],f[701][2],g[701][2];
const int mod=1e9+7;
int calc(int d){
memset(f,0,sizeof f),memset(g,0,sizeof g);
g[0][0]=d;
for(int i=1;i<=n;i++){
for(int k=0;k<=9;k++){
for(int j=0;j<2;j++){
// add i
// j is upper
bool op=(j&(k==t[i]))|(k>t[i]);
if(k>d){
(g[i][op]+=g[i-1][j]*10)%=mod;
(f[i][op]+=f[i-1][j]*10)%=mod;
}else if(k==d){
(g[i][op]+=g[i-1][j])%=mod;
(f[i][op]+=f[i-1][j]*10+g[i-1][j])%=mod;
}else{
//k<d
(g[i][op]+=g[i-1][j])%=mod;
(f[i][op]+=f[i-1][j])%=mod;
}
}
}
}
return f[n][0];
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>s;
n=strlen(s);
reverse(s,s+n);
for(int i=0;i<n;i++)t[i+1]=s[i]-'0';
int ans=0;
for(int i=1;i<=9;i++)ans=(ans+calc(i))%mod;
cout<<ans;
return 0;
}
P3311 [SDOI2014] 数数
我们称一个正整数 是幸运数,当且仅当它的十进制表示中不包含数字串集合 中任意一个元素作为其子串。例如当 时, 是幸运数,、、 不是幸运数。给定 和 ,计算不大于 的幸运数个数。
答案对 取模。
,,,,其中 表示字符串 的长度。 没有前导 ,但是 可能有前导 。
数位 DP 还开这么大的 ,有点吃多了。
Hint
字符串匹配能想到什么?大部分数位 DP 直接把需要的状态塞进去就是对的。
题解
建出 AC 自动机,下放一下 fail 树上的结尾标记,然后直接把 AC 自动机上的节点塞到 DP 状态里面。每次转移判一下目标状态有没有标记。
作者用的不是记忆化搜索,而这道题的前导 对计数有影响,所以我们应该统计转移时首位不为 并且不是枚举到最高位时顶到上界的贡献,然后就做完了。
代码
#include<bits/stdc++.h>
using namespace std;
char s[1505];
int nt[1205],ns[1505];
int t[1505][10],tcnt=1,v[1505];
int fail[1505];
vector<int> E[1505];
const int mod=1e9+7;
int n,m;
int read(int *S){
cin>>s;
int siz=strlen(s);
for(int i=0;i<siz;i++)S[i+1]=s[i]-'0';
return siz;
}
void insert(int *S,int siz){
int now=1;
for(int i=1;i<=siz;i++){
if(!t[now][S[i]])t[now][S[i]]=++tcnt;
now=t[now][S[i]];
}
v[now]|=1;
return;
}
queue<int> q;
void addfail(int u,int v){
fail[u]=v;
E[u].push_back(v),E[v].push_back(u);
return;
}
void getfail(){
for(int i=0;i<10;i++)t[0][i]=1;
q.push(1);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<10;i++){
if(t[u][i]){
int k=fail[u];
while(!t[k][i])k=fail[k];
addfail(t[u][i],t[k][i]);
q.push(t[u][i]);
}else t[u][i]=t[fail[u]][i];
}
}
return;
}
void dfs(int now,int f){
for(auto p:E[now]){
if(p^f){
v[p]|=v[now];
dfs(p,now);
}
}
return;
}
int f[1505][1205][2];
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
n=read(nt);
reverse(nt+1,nt+n+1);
cin>>m;
for(int i=1;i<=m;i++){
int siz=read(ns);
reverse(ns+1,ns+siz+1);
insert(ns,siz);
}
getfail();
dfs(1,0);
f[0][1][0]=1;
int to;
bool op;
int ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=tcnt;j++){
for(int k=0;k<10;k++){
if(v[t[j][k]])continue;
to=t[j][k];
for(int o=0;o<2;o++){
op=(o&(k==nt[i]))|(k>nt[i]);
(f[i][to][op]+=f[i-1][j][o])%=mod;
if(k&&!(i==n&&op))(ans+=f[i-1][j][o])%=mod;
}
}
}
}
cout<<ans;
return 0;
}
P3281 [SCOI2013] 数数
傻逼出题人蚂蚱了。进制和位数全部开 很帅吗。
Fish 是一条生活在海里的鱼,有一天他很无聊,就开始数数玩。他数数玩的具体规则是:
- 确定数数的进制 。
- 确定一个数数的区间 。
- 对于 间的每一个数,把该数视为一个字符串,列出该字符串的每一个(连续的)子串对应的 进制数的值。
- 对所有列出的数求和。现在 Fish 数了一遍数,但是不确定自己的结果是否正确了。由于 较大,他没有多余精力去验证是否正确,你能写一个程序来帮他验证吗?
。
Hint
之前我们的 DP 每次都是 转移的。再回想之前记忆化搜索的状态,这道题中我们能不能 转移而不是枚举这里填什么呢?
题解
我们使用记忆化搜索。
考虑维护当前状态下,所有数的贡献和,所有数的个数,所有数的前缀形成的数的和。转移是简单的,具体可以看代码。
注意到进制是 级别的,我们不能枚举进制来完成转移。但是我们发现状态中没有与该位填什么有关的地方,所以我们只用枚举顶没顶上界来贡献。
可能需要注意前导 带来的影响。
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
int B;
int n,nl[100005],m,T,nr[100005],_B[100005],__B[100005];
int f[100005][2],g[100005][2],h[100005][2];
bool vis[100005][2];
const int mod=20130427;
struct po{int sum,cnt,psum;};
po dfs(int pos,bool lim,const int *t){
if(!pos)return (po){0,1,0};
if(vis[pos][lim]&&pos!=T)return (po){f[pos][lim],g[pos][lim],h[pos][lim]};
vis[pos][lim]=1;
int res1=0,res2=0,li=(lim?t[pos]:B-1),res3=0,cp=(pos==T);
auto p1=dfs(pos-1,0,t),p2=dfs(pos-1,lim,t);
// for(int k=(pos==T);k<=li;k++){//original DP - O(B)
// res1=(res1+p.sum)%mod;
// res2=(res2+p.cnt)%mod;
// res3=(res3+k*p.cnt%mod*__B[pos-1]%mod+p.psum)%mod;
// }
res1=(res1+p1.sum*max((li-cp),0ll)%mod+p2.sum)%mod;//O(1) transfer
res2=(res2+p1.cnt*max((li-cp),0ll)%mod+p2.cnt)%mod;
res3=(res3+((li-1)*li/2%mod*p1.cnt%mod*__B[pos-1]%mod)%mod+p1.psum*max(li-cp,0ll)%mod)%mod;
res3=(res3+li*p2.cnt%mod*__B[pos-1]%mod+p2.psum)%mod;
res1=(res1+res3)%mod;
return (po){f[pos][lim]=res1,g[pos][lim]=res2,h[pos][lim]=res3};
}
int calc(int siz,int *t){
memset(f,0,sizeof f),memset(g,0,sizeof g);
memset(vis,0,sizeof vis);
int res=0;
for(int i=siz;i>=1;i--)res=(res+dfs(T=i,(i==siz),t).sum)%mod;
return res;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>B;
_B[0]=1;
__B[0]=1;
for(int i=1;i<=100000;i++)_B[i]=_B[i-1]*B%mod,__B[i]=__B[i-1]*B%mod+1;
cin>>n;
for(int i=1;i<=n;i++)cin>>nl[i];
reverse(nl+1,nl+n+1);
cin>>m;
for(int i=1;i<=m;i++)cin>>nr[i];
reverse(nr+1,nr+m+1);
//-1
if(n!=1||nl[1]){
for(int i=1;i<=n;i++){
if(!nl[i])nl[i]=B-1;
else{
nl[i]--;
if(nl[i]==0&&n==i)n--;
break;
}
}
}
cout<<(calc(m,nr)-calc(n,nl)+mod)%mod<<"\n";
return 0;
}
接下来就是数位 DP 比较困难的题了。
P3791 普通数学题
一天 zzq 没有题可以出了。于是他随便写了一个式子,求,其中 表示异或。
zzy 一看,这不是水题吗,就随便加了一个函数:,其中 表示异或, 表示 的约数个数。注意 。
现在 zzq 不会做了,只好写了一个暴力造了数据,然后把这道题丢给了你。答案对 取模。
。
Hint
假设我们现在有一个后缀是不定(就是 都可取),前缀定的一个数,它异或上一个数 ,这样的贡献是什么?显然异或并不会影响到后缀的不定性。这样就贡献了约数函数在 处求和得到的值。
解法
观察式子,我们发现在不预处理的情况下求单个 函数和求一段前缀的 函数和都是 的,前者直接枚举,而后者只需要一个整除分块就行。考虑我们把上面的异或规约到几个区间上来处理。
因为异或是不改变某位上可能的值域大小(即不会出现 和 异或某个值的结果是一样的),所以我们结合数位 DP 的思想,把数 拆成 个限制和原数,每个限制的描述是(接下来的位都是二进制位):前 位和原数一样,第 位原数是 ,但是限制其必须为 ,然后剩下的位全部随意填 。首先我们发现单个这个的限制异或上一个数 是简单的,因为异或 对不定的位的可能选的数没有影响,唯一有影响的是前 位,前 位要异或 ,后面仍然是随意填 。
然后考虑把限制扩展到两个数。我们发现假如说我们钦定后缀长度小的那个限制是某个数 ,我们发现任何 异或上另外一个限制的新限制是都是一样的,这一点很好看出来。然后就和上一段讨论的一样了,只不过最后的贡献需要乘上 的后缀长度小的限制的后缀长次幂。
读者或许有疑问,就算这样得到一个限制,怎样计算这样一个限制在 函数上的贡献呢?注意到一个后缀不定的数贡献范围是一个区间。那么整除分块即可。
然后这道题就基本结束了,复杂度 。
但是你发现过不了。但是我们发现一个长度的后缀的限制其实对应的区间只有 种,分别来源于 和 。这个易证,这里不赘述。所以有用的贡献区间是只有 个的。
然后记忆化一下计算过哪些 的前缀,复杂度即可做到 。
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,x;
int ans;
unordered_map<int,int> mp;
const int mod=998244353;
int pd(int num){
if(mp[num])return mp[num];
int res=0;
for(int l=1,r;l<=num;l=r+1){
r=num/(num/l);
res+=((num/l)%mod*((r-l+1)%mod))%mod;
}
assert(res>=0);
return mp[num]=res%mod;
}
int calc(int posx,int posy){
int tpx=n,tpy=m;
if(posx>-1)tpx&=((1ll<<40)-1)^(1ll<<posx);
if(posy>-1)tpy&=((1ll<<40)-1)^(1ll<<posy);
if(posx<posy)swap(posx,posy);
int tp=(tpx^tpy^x)&(((1ll<<40)-1)^((1ll<<(posx))-1));
int l=tp-1,r=tp+(1ll<<posx)-1;
if(posy==-1)return (pd(r)-pd(l)+mod)%mod;
return ((pd(r)-pd(l)+mod)%mod*((1ll<<posy)%mod))%mod;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m>>x;
for(int i=40;i>=-1;i--){
if(i>-1&&!((1ll<<i)&n))continue;
for(int j=40;j>=-1;j--){
if(j>-1&&!((1ll<<j)&m))continue;
if(i!=-1||j!=-1)(ans+=calc(i,j))%=mod;//guding qian i-1 wei i wei 0
}
}
cout<<(ans+pd(n^m^x)-pd((n^m^x)-1)+mod)%mod<<"\n";
return 0;
}
P3303 [SDOI2013] 淘金
小 Z 在玩一个叫做《淘金者》的游戏。游戏的世界是一个二维坐标。 轴、 轴坐标范围均为 。初始的时候,所有的整数坐标点上均有一块金子,共 块。
一阵风吹过,金子的位置发生了一些变化。细心的小 Z 发现,初始在 坐标处的金子会变到 坐标处。其中 表示 各位数字的乘积,例如 。
如果金子变化后的坐标不在 的范围内,我们认为这块金子已经被移出游戏。同时可以发现,对于变化之后的游戏局面,某些坐标上的金子数量可能不止一块,而另外一些坐标上可能已经没有金子。这次变化之后,游戏将不会再对金子的位置和数量进行改变,玩家可以开始进行采集工作。
小 Z 很懒,打算只进行 次采集。每次采集可以得到某一个坐标上的所有金子,采集之后,该坐标上的金子数变为 。
现在小 Z 希望知道,对于变化之后的游戏局面,在采集次数为 的前提下,最多可以采集到多少块金子? 答案可能很大,小 Z 希望得到对 取模之后的答案。
。
byd 感觉前面这两个数位 DP 黑题都有点唐的。大家来尝试自己切一切。
Hint
状态数很小。状态数很小。状态数很小。重要的事情说三遍。作者就栽在这里。
题解
首先注意到可能出现的数位中不包含 。感谢出题人的良心发现。
然后我们发现 函数值只可能被分解为 。用程序打一下表发现只有不到 个数,那么我们可以一次数位 DP 找出来该 值下有多少数。
坐标两维显然是不相关的,所以我们可以把所有 值按出现数个数排序,然后用一个堆就能找出前 大的 ,然后就做完了。
是不是很简单!
代码
#include<bits/stdc++.h>
using namespace std;
#include<ext/pb_ds/hash_policy.hpp>
#include<ext/pb_ds/exception.hpp>
#include<ext/pb_ds/assoc_container.hpp>
using namespace __gnu_pbds;
const int mod=1e9+7,M=2e4+4;
#define ll long long
ll f[M],fcnt;
ll zt[M];
gp_hash_table<ll,int> mp;
struct info{
int x,y;//x>=y
inline bool operator <(const info &a)const{return 1ll*f[x]*f[y]<1ll*f[a.x]*f[a.y];}
};
priority_queue<info> q;
ll cn[16][M][2],k;
bool vis[16][M][2];
int t[16],tcnt;
ll n;
ll dfs(int pos,int nzt,bool lim){
if(!pos)return (nzt==1);
if(vis[pos][nzt][lim])return cn[pos][nzt][lim];
vis[pos][nzt][lim]=1;
int li=(lim?t[pos]:9);
ll res=0;
for(int i=1;i<=li;i++){
if(zt[nzt]%i)continue;
res+=dfs(pos-1,mp[zt[nzt]/i],lim&(i==li));
}
return cn[pos][nzt][lim]=res;
}
void init(){
ll num=n;
while(num){t[++tcnt]=num%10;num/=10;}
for(int p=1;p<=tcnt;p++)for(int i=1;i<=fcnt;i++)f[i]+=dfs(p,i,(p==tcnt));
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k;
for(ll i2=1;i2<=n;i2<<=1){
for(ll i3=1;i3<=n&&i2<=n/i3;i3*=3){
for(ll i5=1;i5<=n&&i5<=n/(i2*i3);i5*=5){
for(ll i7=1;i7<=n&&i7<=n/(i2*i3*i5);i7*=7){
zt[++fcnt]=i2*i3*i5*i7;
}
}
}
}
sort(zt+1,zt+fcnt+1);
for(int i=1;i<=fcnt;i++)mp[zt[i]]=i;
init();
sort(f+1,f+fcnt+1,greater<int>());
q.push((info){1,1});
ll ans=0;
while(k--){
if(q.empty())break;
info u=q.top();q.pop();
ans=(ans+f[u.x]%mod*f[u.y]%mod)%mod;
if(u.x!=u.y){
if(k)ans=(ans+f[u.x]%mod*f[u.y]%mod)%mod,k--;
else continue;
}
if(u.x==fcnt)continue;
if(u.x==u.y)q.push((info){u.x+1,u.y+1});
q.push((info){u.x+1,u.y});
}
cout<<ans;
return 0;
}
CF582D Number of Binominal Coefficients
给定质数 和整数 ,求满足 且 的数对 的个数。
,,答案对 取模。
这是作者认为的数位 DP 魔王,同时也是 DP 第一部分的最后一道题。
题外话:苹果要来了,这个课件看样子没用了(
旧题重提。
Hint
之前 zfy 的课件中提到过一个叫库默尔定理的东西,这道题跟这个定理有很大关系。
题解
首先我们有库默尔定理: 中,质数 的幂次为 在 进制下的进位数。
你问这怎么证明?利用勒让德定理,有 ,直接把组合数拆开,有 ,带入即可直接得证。
你问勒让德定理怎么证明?作者摆烂了,可以去翻 zfy 课件。
那么这道题变成了求 ,且在 进制下进位次数大于等于 的 的有序对数。
注意到 最多是 左右就无解了,所以我们实际上可以直接数位 DP,设 表示前 位进位次数为 ,当前是否有进位,是否超过上界的方案数。转移不难发现是可以 的,不过较为复杂,具体可以参考代码及注释。
代码
#include<bits/stdc++.h>
using namespace std;
int A[1005],P[3505],tmp[1005],tcnt,pcnt;
int f[3505][3505][2][2];
void DIV(int *a,int siz,int num){
memset(tmp,0,sizeof tmp);tcnt=siz;
bool o=1;long long tp=0;
for(int i=siz;i>=1;i--){
tp=(10ll*tp+a[i]);
tmp[i]=tp/num;
if(o&&!tmp[i])tcnt--;
else o=0;
tp=tp%num;
}
return;
}
int MOD(int *a,int siz,int num){
int tp=0;
for(int i=siz;i>=1;i--)tp=(10ll*tp+a[i])%num;
return tp;
}
int p,al,n;
const int mod=1e9+7;
inline int S(int num){return num<0?0:1ll*(num)*(num+1)/2%mod;}
int T(int L,int R){
if(L>R)return 0;
if(R<p)return (S(R+1)-S(L)+mod)%mod;
return (S(2*p-1-L)-S(2*p-1-R-1)+mod)%mod;
}
int T0(int L,int R){
if(L>R)return 0;
if(R<p)return (S(R-1)-S(L-2)+mod)%mod;
return (S(2*p-1-L)-S(2*p-1-R-1)+mod)%mod;
}
int _T(int L,int R){
if(L>R)return 0;
if(R<p-1)return (S(R+1)-S(L)+mod)%mod;
return (S(2*p-1-L)-S(2*p-1-R-1)+mod)%mod;
}
int _T0(int L,int R){
if(L>R)return 0;
if(R<p-1)return (S(R-1)-S(L-2)+mod)%mod;
return (S(2*p-1-L)-S(2*p-1-R-1)+mod)%mod;
}
int ksm(int a,int b){
if(!b)return 1;
return 1ll*(b&1?a:1)*ksm(1ll*a*a%mod,b/2)%mod;
}
long long ans;
char c;
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>p>>al;
if(al>=3500)return cout<<0,0;
n=1;
while(cin>>c)A[n++]=c-'0';
n--;
reverse(A+1,A+n+1);
while(n){
P[++pcnt]=MOD(A,n,p);
DIV(A,n,p);
n=tcnt;
memcpy(A,tmp,sizeof A);
}
// cout<<pcnt<<"\n";
// for(int i=pcnt;i>=1;i--)cout<<P[i];
f[0][0][0][0]=1;
for(int i=1;i<=pcnt;i++){
for(int j=0;j<=pcnt;j++){
//i-1,j TO
//i-1 j 0 0 to i * 0 0 <=P[i]
(f[i][j][0][0]+=1ll*T(0,P[i])*f[i-1][j][0][0]%mod)%=mod;
//i-1 j 0 0 to i * 1 0 P - P+P[i]
(f[i][j+1][1][0]+=1ll*T(p,p+P[i])*f[i-1][j][0][0]%mod)%=mod;
//i-1 j 0 0 to i * 0 1 P[i]+1 P-1
(f[i][j][0][1]+=1ll*T(P[i]+1,p-1)*f[i-1][j][0][0]%mod)%=mod;
//i-1 j 0 0 to i * 1 1 P+P[i]+1 2P-2
(f[i][j+1][1][1]+=1ll*T(p+P[i]+1,2*p-2)*f[i-1][j][0][0]%mod)%=mod;
//i-1 j 0 1 to i * 0 0 -> <P[i]
(f[i][j][0][0]+=1ll*T(0,P[i]-1)*f[i-1][j][0][1]%mod)%=mod;
//i-1 j 0 1 to i * 0 1 -> P[i] P-1
(f[i][j][0][1]+=1ll*T(P[i],p-1)*f[i-1][j][0][1]%mod)%=mod;
//i-1 j 0 1 to i * 1 0 -> P - P+P[i]-1
(f[i][j+1][1][0]+=1ll*T(p,p+P[i]-1)*f[i-1][j][0][1]%mod)%=mod;
//i-1 j 0 1 to i * 1 1 -> P+P[i] - 2P-2
(f[i][j+1][1][1]+=1ll*T(p+P[i],2*p-2)*f[i-1][j][0][1]%mod)%=mod;
//i-1 j 1 0 to i * 0 0 -> 0 - P[i]-1
(f[i][j][0][0]+=1ll*_T(0,P[i]-1)*f[i-1][j][1][0]%mod)%=mod;
//i-1 j 1 0 to i * 0 1 -> P[i] P-2
(f[i][j][0][1]+=1ll*_T(P[i],p-2)*f[i-1][j][1][0]%mod)%=mod;
//i-1 j 1 0 to i * 1 0 -> P-1 P+P[i]-1
(f[i][j+1][1][0]+=1ll*_T(p-1,p+P[i]-1)*f[i-1][j][1][0]%mod)%=mod;
//i-1 j 1 0 to i * 1 1 -> P+P[i] 2P-2
(f[i][j+1][1][1]+=1ll*_T(p+P[i],2*p-2)*f[i-1][j][1][0]%mod)%=mod;
//i-1 j 1 1 to i * 0 0 -> 0 - P[i]-2
(f[i][j][0][0]+=1ll*_T(0,P[i]-2)*f[i-1][j][1][1]%mod)%=mod;
//i-1 j 1 1 to i * 0 1 -> P[i]-1 P-2
(f[i][j][0][1]+=1ll*_T(P[i]-1,p-2)*f[i-1][j][1][1]%mod)%=mod;
//i-1 j 1 1 to i * 1 0 -> P-1 P+P[i]-2
(f[i][j+1][1][0]+=1ll*_T(p-1,p+P[i]-2)*f[i-1][j][1][1]%mod)%=mod;
//i-1 j 1 1 to i * 1 1 -> P+P[i]-1 2P-2
(f[i][j+1][1][1]+=1ll*_T(p+P[i]-1,2*p-2)*f[i-1][j][1][1]%mod)%=mod;
}
}
for(int i=al;i<=pcnt;i++)ans=(ans+f[pcnt][i][0][0])%mod;
cout<<ans;
return 0;
}
本文作者:xingyu_xuan
本文链接:https://www.cnblogs.com/xingyuxuan/p/18199177
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步