THUSC 前的吃史记录
前言
史也分好坏。
本文的 Day 1 \(\Leftrightarrow\) 2024/04/13
Day 1
T1 Burnside 群论计数，再见。
T2 一个神秘转图问题，然后用 DP 构造一个有向基环森林。
看懂了。
就是你发现如果我们对于一个二元组 \((u,v)(u,v\in \Sigma)\)，如果 \(u\not= v\)，我们设这个二元组的权值为 \(c\) 加上 \(s_i=u\) 且 \(t_i\not = v\) 的个数。代表假如说我要进行 \(u\to v\) 的全字母操作然后把 \(u\) 全部还原的代价，所以我们发现 \((u,u)\) 的权值不用加 \(c\)。
我们注意到一定存在一种排列方式，使得全字母修改的操作先做完，再一个一个的改。因为如果在全字母修改的时候还进行了单字母修改，我们一定能在最后把这个字母改为正确的字母。
那么我们把这个问题转化成了在我们整出来的一个有向完全图中选出一个有向基环森林。不难想到直接按边权少的选。选出来的图在下文中简称原图。
但是原图中的某些情况是不能直接转移的，因为选到一个位置的时候，如果这里还未执行转移，那么刚刚转移过来的东西会被全部在转移到另一个地方，我们一个一个讨论：
- 根自环树
按深度从浅到深转移即可。
- 非纯环基环树
画张图：
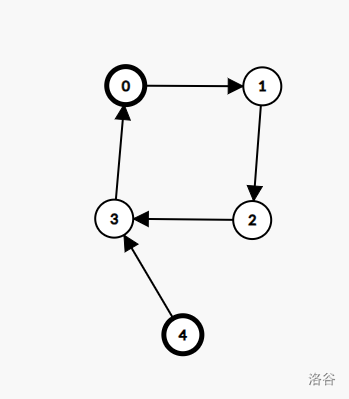
不难发现如果没有点 \(4\)，这个图是无法转移的。
但是存在点 \(4\) 之后就有一线生机了。
我们可以先进行 \(2\to 4\)，然后环上就能转移了。最后....../shui 不写了，因为出题耽搁了一点时间。
Day 4
T3,T4 爆炸。
T1 Hall 定理板子。Hall 定理描述的就是对于一个二分图，是否存在一个完美匹配的条件就是对于某部点的任何一个子集，其与另外一部点中有连边的点集合要大于等于这边子集的大小。
按字典序尝试填入原序列中，用 Hall 定理判定即可。
时间复杂度 \(O(|\Sigma|^{O(1)}2^{|\Sigma|}n)\)。
考拉有一个神秘做法，看了一会儿后没看懂，放弃。
好像就是从后往前预处理判定，然后再在前面填。
T2 简单网络流，注意没有朋友的单点这个 corner。
Day 6
T1 小丑了。我是倒着枚举，少枚举了一部分重复的过程。正解正着枚举，不确定的直接暴力填不知道，发现其实这一部分重复的过程在模 \(2\) 意义下根本不用考虑，所以情况数少了一半，复杂度为 \(O(2^{\frac{n}{2}}(m+n^2))\)。
T2 会 30p，但是由于之前讲课的时候掉线了，所以痛失 30p：
对于所有 \(n\) 阶排列 \(p\)，在其中任意选取一个排列，如果要保证 \(S\) 集合内的元素全部在某个元素 \(k(k\not\in S)\) 后面，那么概率是 \(\frac{1}{|S|+1}\)。
而考场上我是这样的：
根本不知道该怎么化简。
而且 30p 也写挂了，因为我把顺序搞反了。
首先显然这个能化成一个每个点出度最多为 \(2\) 的 DAG，然后把排列贡献转为点贡献，也就转成了上面那个问题和 DAG 上某点可以被其他点可达的计数问题，场上想到了 bitset 优化，时间复杂度 \(O(\frac{n^2}{\omega})\)，加上树的部分分就有 60p。
然后正解就是利用 DAG 性质倍增。
回到原来的图，我们可以从高向低 DP 求出每个线段能到达它的最左边的左端点（右边其实也可以要）。然后我们考虑设一个线段的左父亲为其左端点向上的碰到的第一个线段，右父亲为其右端点向上碰到的第一个线段，那么我们把这个图画出来：
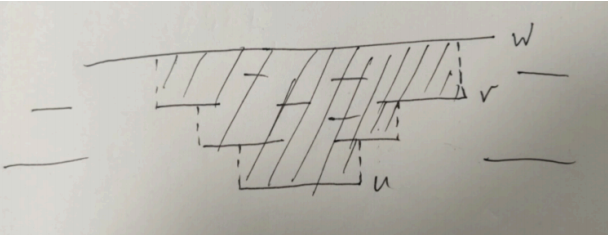
发现 \(w\) 其实就是第一个小于我们刚刚算的那个左端点的左祖先，这个可以倍增求的。
然后就是如何计算中间的阴影部分中有多少条线段。我们其实可以把它拆成一个线段到其左父亲的由其左端点向上的那个线段向左的扫到的那个区域的所有线段，右父亲同（不过这里要加上自己）的差。这个扫描线易求，就是扫右端点，端点是询问，询问在先。这里要求反向的左右父亲（正向的用来 DP）。算出来之后挂在倍增数组上，在倍增同时求和就行了。
时间复杂度为巨大常数 \(O(n\log n)\)。
T3 放置，明天我要研究 NTT 了。
话说这样真的好吗，就这样的话，强的人会补题补得快，可以进行自己的学习，像我这种垃圾的人就补题补得巨慢，然后可能没有时间进行自己的学习，然后导致想要超越就只能寄希望于 强的人变强比弱的人变强慢 这句话？感觉比较极端。
Day 8
乐子场。
T2 是之前我没补的一道虚树 + 根号重构。T3 是之前我没补的一道 lxl 讲课题。
T1 是乐子最小环。枚举断掉每条边，然后边用 BFS 最小环计数。最后答案注意要除以环长。
T4 是乐子 DS。sub1 用线段树，sub2 直接 \(mid\) 左右处理前后缀，sub3 猫树。
注意到这个题其实可以有一个非常好的扩展，这个我会写一个博客。
不过我得感谢这场比赛，让我学会了最小环的简单做法和猫树。
虚树直接因为这场比赛被 push_front() 了。/xk
Day 11
T2 T3 神秘题，看样子不可补（轮廓线和上次 Hanghang 那个重标号题（这个是个论文题））
T1 问了半天后面的做法，大家没有回应，我猜这东西也没什么用，也就不浪费大家时间了。这里就浅浅写一下那个求和的做法。
注意到这个操作可以把数字 \(n\) 变为 \((n-k)\times 2^k\)。（考场上没看出来这一点/xk）
为了去重，显然我们只需要统计 \(n-k\) 为奇数的情况，因为当 \(n-k\) 为偶数时，\(\left(\frac{n-k}{2}\right)\times 2^{k+1}\) 是等价的，而它对应的原数字为 \(\frac{n-k}{2}+k+1\leq n\)，所以只统计奇数又保证了去重，又保证了最小。
因为我们保证了两两不同，所以显然我们求出最小的 \(\sum a_{i}\) 对应的序列的重排后的结果一定可以看做一个相邻两项的差等于 \(0\) 或 \(1\) 的数列。因为只统计奇数，所以对于一个数 \(n\)，它能变成 \(\left\lceil\frac{n}{2}\right\rceil\) 个不同的数。
所以这个问题就变成了：每个数 \(i\) 能最多生成 \(\left\lceil\frac{i}{2}\right\rceil\) 个数，生成一个数的代价就等于原数字的值，问生成 \(n\) 个数所需要的最小代价。推推式子即可。
\(\left\lceil\frac{i}{2}\right\rceil\) 个数生成满的 \(i\) 的前缀的贡献和的式子：
最后需要分讨一些情况。
笑点解析：我不会算 \(\sum_{i=1}^{n-1}i(n-i)\)，然而拆出来就等于 \(n\sum_{i=1}^{n}i-\sum_{i=1}^{n}i^2\)。
Day 13
根本补不完专题。
时间总是够的，挤一挤就有了。
我希望这句话是对的，虽然我的希望顶个空气。唉。
T1 Min_25 筛，再见。
T3 神秘巨大 DP，再见。
T4 sb 遗传 + 玄学规律，再见。
T2 还好一点，感觉其实比较诈骗，和上次的 CF1621H 差不多。
考虑我们使用 Trie（我考场上一直在想拆位线段树/xk）来维护，因为我们可以把这个东西拆成两个数相异或的形式：\(pre_{r}\oplus pre_{l-1}\)，然后就可以 Trie 做了。
我们就只需要判断在一个地方能不能向左走或者向右走即可。我们可以考虑容斥。对于三元组 \((x,y,z)\)，\(x\) 代表膜第一个人的次数，\(y\) 代表膜第二个人的次数，\(z\) 代表膜第三个人的次数。我们设 \(a=x-y,b=y-z,c=x-z\)，那么我们对于区间 \([l,r]\)，它满足限制的条件是 \(a_{l-1}\not= a_{r},b_{l-1}\not=b_{r},c_{l-1}\not=c_{r}\)。因为 \(a+b=c\)，所以我们可以维护一个容斥的结果，即我们维护全集和 \(a_{l-1}=a_{r}\)，\(b_{l-1}=b_{r}\)，\(c_{l-1}=c_{r}\) 的并集。而因为这个并集是和 \(a,b,c\) 当前的值有关的，所以实际上要开最多 \(4n+1\) 个 Trie，然后在 \(O(1)\) 个 Trie 上验证哪边能走。
但是这里就是比较诈骗的地方了：我们其实可以对于每个节点维护这个节点有哪些三元组是不能进去的。我们考虑这个最大是多少。我们发现如果有完全不同的三元组 \((a,b,c)\) 一共四个（其内部所有元素均两两不同），那么就一定有解。而如果定了 \(a\)，那么就只用 \(3\) 个完全不同的 \((b,c)\) 就能确定有解，所以我们可以维护 \(3\) 个不同 \(a\) 值，每个 \(a\) 值里面最多维护 \(2\) 个不同的 \(b\) 值（注意维护的所有 \(b\) 值必须要保证互不相同），而 \(a+b=c\)，所以这个时候就维护完了。而一旦某一处超过了其阈值，我们就标记这一块都有解。一共 \(6\sim 9\) 个元素，卡空间后是能够通过的。但是细节较多，上面的讲述也可能并不全面。
这里给出一个不需要 \(a+b=c\) 性质的做法。考虑我们引入一个通配符的概念，就是某一位是通配符时，这一位填什么与其是否满足条件没有关系。那么我们可以直接维护 \(6\) 个三元组，虽然空间看起来不是能过的样子，但是有人过了。
具体过程就是：我们维护的三元组是任意一个三元组和询问三元组完全一致时才能判定这个位置能不能走。考虑首先是对于不变的情况，假如说我们现在有一个 \((a,b,c)\) 的三元组作为限制，那么加入 \((a,x,y)\) 这个三元组的某个值的时候你会发现 \((a,b,c)\) 的限制对 \((a,x,y)\) 依然有效，于是要保留 \((a,b,c)\) 这个限制。而如果插入 \((x,y,z)\)，对于 \((a,b,c)\) 没有关系时，那么这个限制显然没用了。
上面的情况显然不适用于通配符存在时，假如说我们存在一个 \((A,B,C)\) 的限制，插入 \((x,y,z)\)，如果 \(A\) 是通配符，这里多了一个 \(x\) 的限制，那么我们如果第一位填 \(x\) 之外的东西，然后剩下的东西满足 \(B,C\) 的限制，那么就有可能可以通过 \((x,y,z)\) 进入这里，所以需要修改这个限制。而我们发现，我们可以把这个限制分出一个 \((x,B,C)\) 的限制，因为显然如果第一位等于 \(x\)，它等价于原来的和新插入的限制。对于 \(B,C\) 同样做一遍这样的操作。当然，显然当 \(A=x\) 或 \(B=y\) 或 \(C=z\) 的时候，我们就可以直接保留这个限制了，不需要进行这里说的对通配符的操作。
对于没有保留的限制就直接扔掉，发现我们最多只有 \(6\) 个三元组的限制。
以上方法的时间复杂度均为 \(O(n\log n)\)。这里我们实现一下最后一个做法。
Day 16
不写题解了，休息一下。
Day 23(?)
T1 单 log 是暴力/yiw，我是超级钢琴 + 主席树维护可持久化 hash 数组 + 主席树上二分做的，两个 log。
T2,3,4 爆炸。
Day 24
T1 exchange arguments 贪心。
T2 PGF，再见。
T3 lxl 神秘题目，再见。
你就这样考吧，反正我不会，也没时间补完，只能一个板块一个板块的整，我还要做我的课件。如果硬说时间够的话，那我就肯定要挤晚上的时间了，然后早上的时候我就会变成第二个 Meatherm。
T1 是一个比较牛牛的题，需要将删除化为合并，然后这个合并很特殊，每次我们选一个联通块的根和其父亲所在联通块合并，代表父亲那个联通块执行完所有删除之后就立即来删这个联通块。这个时候这两个联通块就合并称为了一个联通块。然后就可以 exchange arguments 做了。这个东西其实就是一个套路，在最优解的基础上任意交换相邻两个元素，然后写出其优不优的条件，然后就可以解出一个关系式，通常这个关系式可以被排序。
考虑我们其实此时可以钦定 \(a,b\) 的父亲均已被删除，我们需要选出 \(a,b\) 中性价比更高的那个，假设 \(a\) 要放在 \(b\) 前面，那么有（设 \(a_0,a_1\) 为 \(a\) 联通块中 \(0,1\) 的个数，\(b\) 是一样的）：
其中前面是 \(a\) 对 \(b\) 的逆序对贡献，后面为 \(b\) 对 \(a\) 的逆序对贡献。这里我们也能解释为什么不能通过删点来贪心，因为我们对于删点，我们无法确定这个联通块到底是什么。然后倒着合并正好也能刻画删点时候，在两次删掉同一棵子树之间夹了一个删其它子树的情况。
然后我们用并查集合并一手两个联通块，然后我们删除原来的父亲和儿子，然后插入新的合并过后的联通块就行了。
Day 27
我想睡觉了。
Day 28
羡慕大家补题的速度。
T3 找规律。
T1 把排列拆成矩阵，\(a_{i,j}=[p_i<p_j]\)，维护概率，离散化后 \(O(n+m^2)\) 初始化，后面模拟即可。询问就求 \(l,r\) 的列和。
只需要维护 \(O(m)\) 条长条的信息，还有 \(O(m)\) 条列组的和信息。好像只能每个块都建一个数组，我开始的时候对于长条建的建了两个数组，后面发现不行，于是就没写了。
