5. 线性回归-pytorch实现
1. 本篇博客参照第四篇的步骤,使用pytorch实现的:
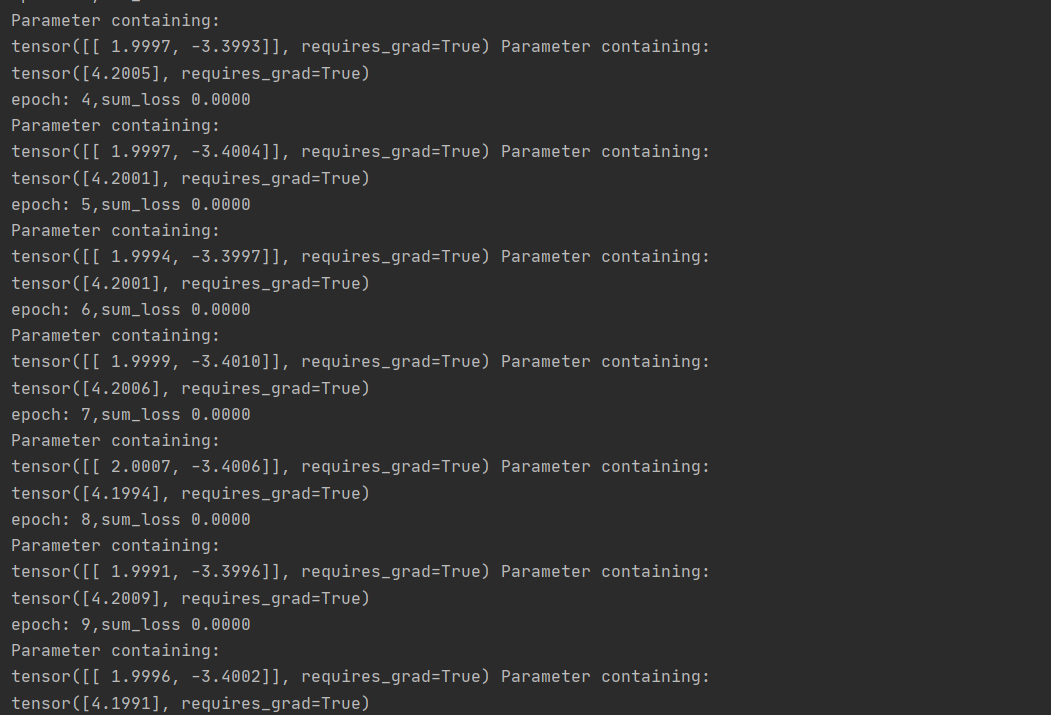
1 import numpy as np 2 import torch 3 import torch.utils.data as Data 4 from torch import nn 5 import torch.nn.init as init 6 # 数据集生成 7 8 num_inputs = 2 9 num_samples = 1000 10 true_weight = torch.tensor([[2],[-3.4]]) 11 true_bais = torch.tensor([[4.2]]) 12 13 features = torch.randn(num_samples,num_inputs,dtype=torch.float) 14 labels = torch.mm(features,true_weight)+true_bais 15 labels += torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float) 16 # 数据读取 17 batch_size = 100 18 train_data =Data.TensorDataset(features,labels) 19 dataiter = Data.DataLoader(train_data,batch_size,shuffle=True) 20 #for x,y in dataiter: 21 #print(y) 22 # 定义模型 23 class LineNet(nn.Module): 24 def __init__(self,n_features): 25 super(LineNet, self).__init__() 26 self.linear = nn.Linear(n_features,1) 27 28 def forward(self,x): 29 return self.linear(x) 30 31 net = nn.Sequential( 32 nn.Linear(num_inputs,1) 33 ) 34 print(net[0]) 35 #for params in net[0].parameters(): 36 #print(params) 37 # 初始化模型参数 38 w = init.normal_(net[0].weight,mean=0,std=0.01,) 39 b = init.constant_(net[0].bias,val=0) 40 #定义损失函数 41 loss = nn.MSELoss() 42 #定义算法优化 43 optimzer = torch.optim.SGD(net[0].parameters(),lr=0.3) 44 #训练模型 45 def train_module(data_iter,epoches): 46 for epoch in range(epoches): 47 sum_loss,n = 0.0,0 48 for x, y in data_iter: 49 y_hat = net(x) 50 l = loss(y_hat,y.view(-1,1)) 51 52 optimzer.zero_grad() 53 l.backward() 54 optimzer.step() 55 n += y.shape[0] 56 sum_loss += l.sum().item() 57 print('epoch: %d,sum_loss %.4f '%(epoch, sum_loss/n)) 58 print(net[0].weight,net[0].bias) 59 60 train_module(dataiter,10)
2. 相关知识补充:
-
从上一节从零开始的实现中,我们需要定义模型参数,并使用他们一步步描述模型是怎样计算的。当模型结果变得复杂时,这些步骤变得更加繁琐。其实pytorch提供了大量的预定义的层,这使我, 只需要关注使用哪些层来构造模型。下面介绍pytorch更加简洁的定义线性回归。
-
首先导入torch.nn 模块,实际上,nn是neural network的缩写。该模块定义了大量神经网络的层,之前使用过的autograd,而nn就是利用autograd来定义模型。
-
nn的核心数据结构是Module,它是一个抽象概念,既可以表示神经网络中的某个层,也可以表示包含很多层的神经网络。
-
在实际使用中,通过会继承torch.Module,撰写自己的网络/层。一个nn.Module实例应该包含一些曾以及返回输出的前向传播(forward)方法.
1 # 定义模型 2 class LineNet(nn.Module): 3 def __init__(self,n_features): 4 super(LineNet, self).__init__() 5 self.linear = nn.Linear(n_features,1) 6 7 def forward(self,x): 8 return self.linear(x)
######重点:
还可以用nn.Sequential来更加方便的搭建网络,Sequential是一个有序的容器,网络层将按照在传入的Sequential的顺序依次被添加到计算图中:
1 # 写法1 2 net= nn.Sequential(nn.Linear(num_inputs,1) 3 # 此处还可以传入其他的层 4 ) 5 # 写法2 6 net = nn.Sequential() 7 net.add_module('linear',nn.Linear(num_inputs,1)) 8 # net.add_module ..... 9 10 11 # 写法3 12 13 from collections import OrderedDict 14 15 net = nn.Sequential( 16 OrderedDict([ 17 ('linear',nn.Linear(num_inputs,1)) 18 # 其他的层 19 20 ]) 21 ) 22 23 print(net) 24 print(net[0]) 25 26 Sequential( 27 (linear): Linear(in_features=2, out_features=1, bias=True) 28 ) 29 Linear(in_features=2, out_features=1, bias=True) 30 for param in net.parameters(): 31 print(param) 32 Parameter containing: 33 tensor([[-0.4229, -0.0282]], requires_grad=True) 34 Parameter containing: 35 tensor([0.0852], requires_grad=True)
#####上述写法:我一开始想访问每次2迭代后访问参数,用的net = LinearNet(num_inputs),没有想出来怎么访问,才使用的后面的这种方式,至于为什么这种方式可以,我也不知到,希望在后续的学习中可以了解到


