递归

介绍递归

　　递归——函数自己调用自己。递归有时难以捉摸，有时却很方便实用。如果结束递归是使用递归的难点，如果递归代码中没有终止递归的条件测试部分，一个调用自己的函数会无线递归，这会造成很大的麻烦。

　　可以使用循环的地方通常都可以使用递归。有时候循环解决问题比较好，有时候递归更好。递归方案更简洁，但效率没有循环高。

　　

演示递归

#include<stdio.h> 
void up_add_down(int);

int main(){
    up_add_down(1);
    puts((char[]){"下午好"});
    
    
    return 0;
}

void up_add_down(int n){
    printf("Level %d: n location %p\n", n, &n);　　//#1
    if(n < 4)
        up_add_down(n + 1);
    printf("Level %d: n location %p\n", n, &n);   //#2

}

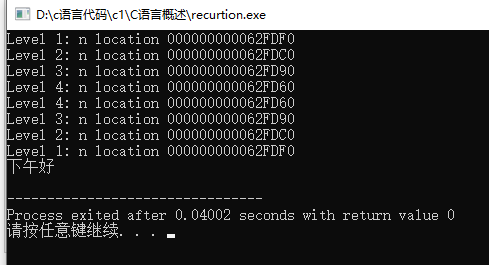
　　首先，main()调用了形参为1的up_add_down()，先执行注释为#1的句子，为1级调用，然后if判断，n不大于4，则调用函数本身并形参加一（n + 1），为2级调用。这样一直循环，直到不满足if条件，执行递归后执行注释为#2的句子，此时n = 4，4级调用结束，然后控制被传回它的主调函数（即第三级调用）。在第三级调用中，执行的最后一条语句是up_add_down(n + 1)（此时n = 3)，所以又执行了一次#2，之后以此类推，2级调用返回Level 3。。。。和Level 2。。。

　　如果觉得不好理解。可以假设有一个函数调用链——fun1()调用fun2()， fun2()调用了fun3()，fun3()调用了fun4()。当fun4()结束时，控制传回fun3()；当fun3()结束时，控制返回fun2()。。。直到回到1级调用fun1()

 

 

递归的基本原理

　　1、每级函数都有自己的变量。1级的n和2级的n不同，所以程序创建了4个单独的变量，每个变量名都是n，但是它们的值各不相同。当程序最终返回1级调用时，此时的n依然是它的初值1。

　　2、每次函数调用一次就会返回一次，当函数执行完毕后，控制权将被传回上一级递归，程序必须按顺序逐级返回递归，不能从4级跳到1级。

　　3、递归函数之前的语句，均按被调函数顺序执行。

 

　　4、递归函数之后的语句，均按被调函数相反的顺序执行。递 归调用的这种特性在解决涉及相反顺序的编程问题时很有用。

　　5、虽然每级递归都有自己的变量，但是没有拷贝函数的代码。程序按顺序执行函数中的胆码，而递归调用就相当于又从头开始执行函数的代码。类似于循环，所以有时它们之间可以互相替换。

　　6、递归函数中必须包含停止递归的语句（循环也一样）。通常，递归函数使用If或其他等价的测试条件在函数形参等于某个特定值时终止递归。为此每次递归调用的形参都要是不同的值。

 

 

尾递归

　　最简单的递归形式——把递归调用置于函数的末尾，即正好在return语句之前。这种形式的递归被称为尾递归，相当于循环，下面例子用循环和递归两种方式计算正整数的阶乘。

#include<stdio.h> 

int for_factorial(int n);
int recution_factorial(int n);

int main(){
    puts((char[]){"晚上好"});
    printf("%d\n", for_factorial(3));
    printf("%d\n", recution_factorial(3));
    
    return 0;
}

int for_factorial(int n){
    int i;
    long num = 1;
    for(i = 2; i <= n; i++){
        num *= i;
    }
    return num;
}

int recution_factorial(int n){
    long num;
    if(n > 0)
        num = n * recution_factorial(n - 1);
    else
        num = 1;
    return num;
}

　　注意，尾递归不一定是在最后一行，而是最后一条执行的语句，这个函数的关键是：n!  =  n * (n - 1)!。可以这样是因为(n - 1)!是n-1 ~ 1的所有正整数的乘积。阶乘的这一性质很适合使用递归。

　　既然循环和递归都能解决问题，那到底该用那一个呢，一般而言循环好一些恶。首先：每次递归都会创建一组变量，所有递归的内存消耗更多，而且每次递归调用调用都会把创建的一组新变量存放入栈中，递归调用的数量受限于内存空间的大小，其次，每次函数调用都要花费一定时间，所以执行的速度相对慢。但是在某些情况下，递归比循环更加适合于方便，因此要好好理解递归。

 

 

递归和倒序计算

　　递归在处理倒序时非常方便。我们要解决的问题是：编写一个函数，打印一个整数的二进制数。二进制表示法根据2的幂来表示数字。

　　我们要设计一个以二进制形式表示整数的算法。例如，如何用二进制表示5？在二进制中，奇数的末尾一定是1，所以通过5 % 2既可以确定5的二进制最后一位。一般而言，对于数字n，其二进制的最后一位是n % 2.因此，计算机得出的第一位数字其实是二进制数的最后一位。这一规律提示我们，在递归调用之前计算n % 2，在递归调用之后打印的计算结果。这样，计算的第一个值正好是最后一个打印的值。

　　要获得下一位数字，必须吧原数除以2.这样计算方法相当于在十进制下把小数点往左移一位，如果计算结果是偶数。那么二进制的下一位数就是0；是奇数则为1。这样一直递归调用，直到与2相除的结果小于2时停止调用，因为只要结果大于等于2，就说明还有二进制位，每次除2就相当于去除一个二进制位。例子如下

　　

#include<stdio.h> 
void recurtion_binary(unsigned long n);


int main(){
    puts((char[]){"下午好，请输入一个整数"});
    unsigned long n;
    scanf("%d", &n);
    puts("该数的二进制数为：") ;
    recurtion_binary(n);
    return 0;
}

void recurtion_binary(unsigned long n) {
    int r;
    r = n % 2;
    if(n >= 2){
        recurtion_binary(n / 2);
    }
    putchar(r == 0 ? '0' : '1');
}

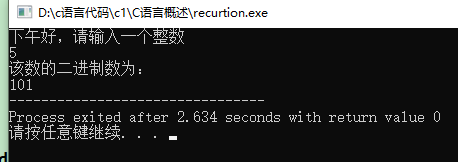
　　不用递归也能用循环来实现，但是要用数组把所有求得的二进制位都保存下来。

 

 

递归的优缺点

 　　优点：为某些编程问题提供了最简单的解决方案。

　　 缺点：一些递归算法会快速消耗电脑的内存资源，不方便阅读和维护。

　　例子：斐波那契数列的定义如下：第一个和第二个数字都是1，而后续的每个数字为前两个数字之和：

#include<stdio.h> 
unsigned long recurtion_fibonacci(unsigned long n);


int main(){
    puts((char[]){"ÏÂÎçºÃ£¬ÇëÊäÈëÒ»¸öÕûÊý"});
    unsigned long n;
    scanf("%d", &n);
    printf("µÝ¹é¼ÆË㣺¸ÃÊýµÄì³²¨ÄÇÆõÊýΪ£º%d\n", recurtion_fibonacci(n));
    printf("Ñ­»·¼ÆË㣺¸ÃÊýµÄì³²¨ÄÇÆõÊýΪ£º%d\n", recurtion_fibonacci(n));
    return 0;
}

unsigned long recurtion_fibonacci(unsigned long n){
    if(n > 2){
        return recurtion_fibonacci(n - 1) +  recurtion_fibonacci(n - 2);
    }else{
        return 1;
    }
}

unsigned long for_fibonacci(unsigned long n){
    int i, now = 1, pare_1 = 1, pare_2 = 0;
    for(i = 1; i < n; i++){
        now = pare_1 + pare_2;
    }
    return now;
}

　　这个递归函数只是重述了数学定义的递归。该函数使用了双递归，即函数每一级递归都要调用本身两次，这暴露了一个问题：1级调用，创建了一个变量n，然后二级调用，要创建两个变量。这两次调用中每次调用又会进行两次调用，因而在三级递归中要创建4个变量n，所以变量的个数呈现指数增长，很可能导致程序奔溃。虽然例子本身很极端，但是说明递归的使用要特别小心，尤其是效率优先的程序。