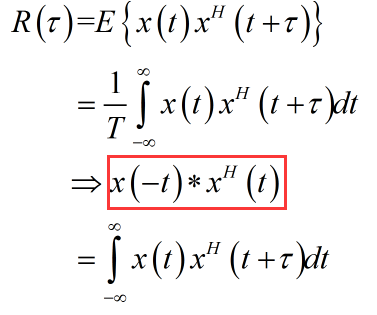工程应用中的自相关操作

作者：桂。

时间：2018-01-10  18:41:05

链接：http://www.cnblogs.com/xingshansi/p/8260315.html 

---

前言

主要记录工程应用中的自相关操作，以及自相关的一些理论性质。

代码实现可参考：Xilinx 常用模块汇总(verilog)【03】

一、自相关函数

自相关的定义式：

实际操作中，通常假设随机信号独立同分布，依托遍历性近似估计R矩阵：

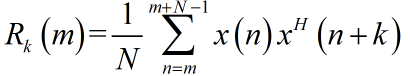
k表示相关函数的时间间隔，m表示起始时刻，N表示截取的时间片。

为了便于表示，假设:

相关矩阵的估计，可以提取系统的响应函数：

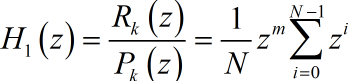
进一步处理系统响应函数：

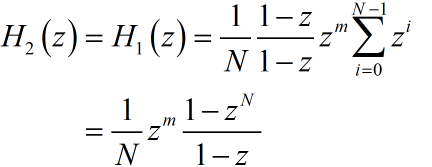
由此得出结论：

重复累加的操作可以通过递归的思路实现，这样一来节省了乘法器资源。

 递归的结构：

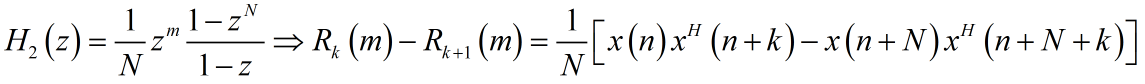
即：

至此便完成了自相关的硬件估计思路：3加法器 + 复数乘法器，即可完成估计。

二、参数的选取

自相关的参数，其影响因素主要包括：对信噪比SNR的提升、兔耳效应的抑制、对窄脉冲的适应能力。

1-对SNR的提升

　　该部分参考：《基于多相滤波的超宽带接收机研究及FPGA实现》。

信号形式定义为：

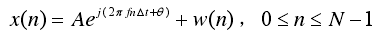
m点自相关：

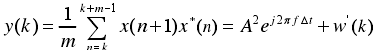
其中

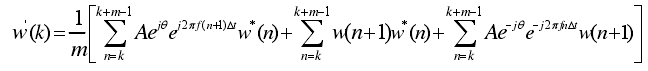
该信号均值为0，方差为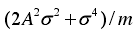，当m>>1时其近似为高斯分布，输出信噪比：

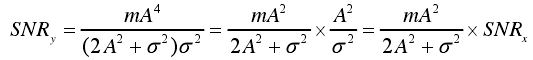
可以看出信噪比增益近似为：，增益的下限由灵敏度及最小检测门限有关。

2-兔耳效应的抑制

　　该部分为优化内容，即使不能严格满足，依然可以借助其他方式改善性能，自相关点数不必严格受此局限。信道化体制下，假设每个信道的滤波器阶数为M0，则兔耳宽度为M0-1，信号宽度为N0（受窄脉冲要求限定），则自相关间隔（第一部分的k值）在M0-1<x<N0，较为理想。

3-对窄脉冲的适应能力

 　　窄脉冲宽度与AD性能决定了信号的数字宽度，此时的间隔k+点数N应<=信号宽度。

 

三、自相关函数与卷积的对应关系

 　　自相关函数的傅里叶变换是功率谱，自相关与卷积具有数学上的关联，二者在硬件实现时可互相借鉴思路：