Chapter 5:Spectral-Subtractive Algorithms

作者：桂。

时间：2017-05-24  10:06:39

主要是《Speech enhancement: theory and practice》的读书笔记，全部内容可以点击这里。

书中代码：http://pan.baidu.com/s/1hsj4Wlu，提取密码：9dmi

---

 一、谱减的基本原理

　　A-基本问题

基本模型是加性噪声：

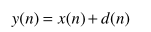
频域模型：

所谓谱减法，可以通过不同的假设进行，一般的：

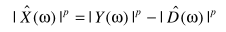
通常为了避免幅值出现负数，加上一个半波整流。这时的幅度估计+带噪信号的相位，即可得出降噪的信号。

　　B-典型

分别取 p = 1, p = 2分析。

p = 1时，谱减

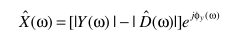
p = 2时，谱减

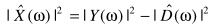
可以看出p = 2是基于统计无关的假设：

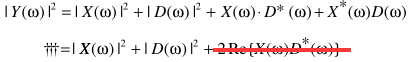
反过来看看p = 1的情形，可以写成：

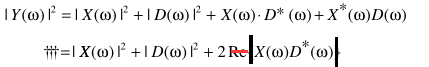
也就是clean信号与noise相位相同，且统计相关。

对比来看，p =  2的假设在应用场景里应该比 p = 1更合理，尽管作为非平稳信号，完全无关的假设难以严格满足。p取其他值的分析类似。

谱减法的基本框架：

 

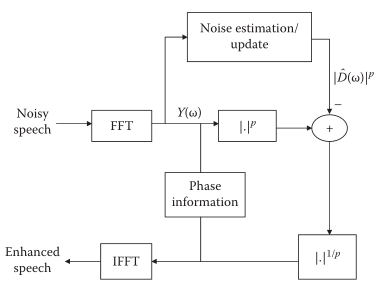
回顾上面的谱减法，理论分析的前提是基于频点，事实上许多应用场景里，noise与clean（特别是在高频区域）满足一定的正交性，即该频点完全属于clean/noise，而非二者的混合，从这一点来说p的不同取值带来的影响远没有理论中体现的那么大。下图也说明了：高频部分的正交性更明显。

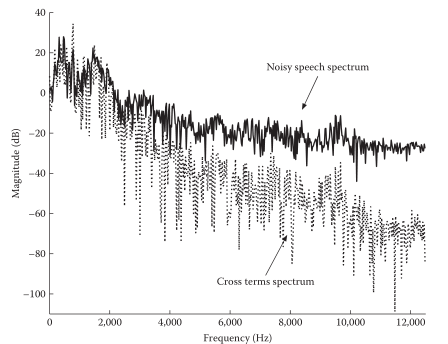
二、谱减法的不足

1-带来了Musical noise

谱减过程中没有完全消除噪声，而把峰值保留了下来，造成Musical noise:

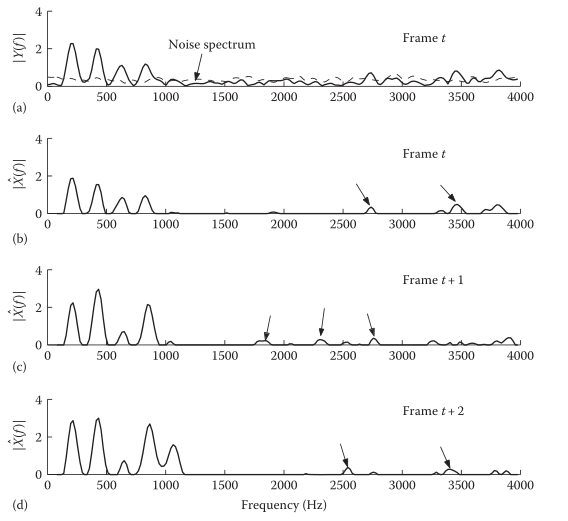
2-相位失真

相位不准确带来的信号失真，带噪的相位来表达clean的相位，造成语音的可懂度下降（书中指出SNRs (<0 dB)，其实这么说是不合适的，噪声与信号正交程度越小，这种论证才有意义）.

三、其它谱减法

　　A-Boll的过减法

Boll的思路其实就是平滑，如果平滑呢？这里没有用线性平滑，而是用了一个min/max{相邻帧信息}的思路,为了防止毛刺：1）谱减的门限D尽可能Max，2）信号的估计尽可能min

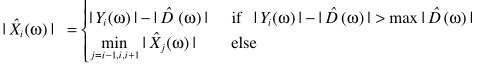
Berouti等人也提出了一种方法：

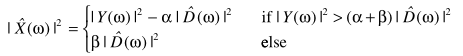
这个思路的核心在于β的选取，其实就是为了减少毛刺引入了填充，其中

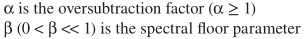，图中可以观察到β的影响：

　　B-非线性谱减

这个的动机是：现实中，噪声对所有频段的影响，并不是均衡的，按上面的思路过于粗糙，例如汽车噪声，可能在某一频段干扰明显，又比如一些噪声对于低频影响更大。非线性谱减的基本规则：

核心在于a(w)不再是一个常数，取值与频率有关。其中的参数一般平滑与处理一下

a通常取非线性函数

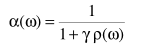
其中ρ

信噪比越大，a越小。 

　　C-多带谱减法

多带谱减也可以归类为非线性谱减，其实就是分自带计算，类似分治法

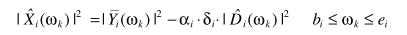
谱减的思路可以按照上面任何一个方法，不同的是用了两个参数：α、，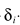

对于α：

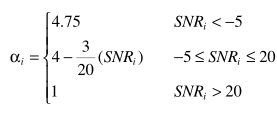
其中

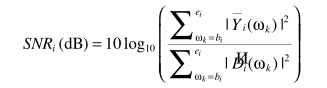
对于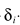

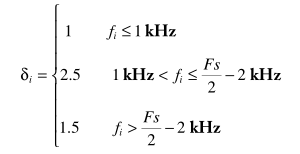
多带的实现框图

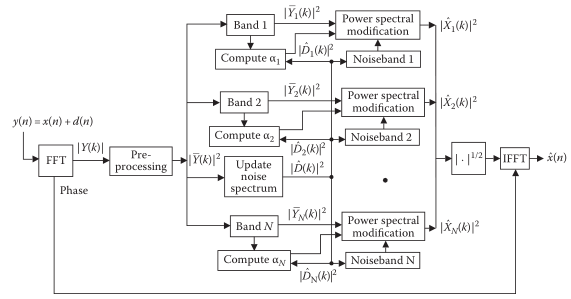
　　D-MMSE谱减法

 上面提到的谱减法，可以有一种广义的定义方式

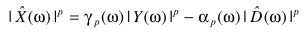且上面的方法都是通过实验经验设定参数，其实对于参数γ、α可以借助MMSE（最小均方误差估计）/其他准则合理即可：

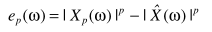
得出的参数估计(细节可参考这里)

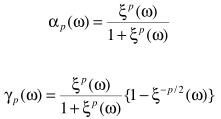
其中

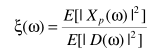
从而得出降噪结果:

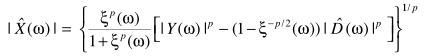
这里用到一个粗糙但简便的假设：噪声谱与干净信号谱的相位相同。

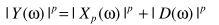
如果假设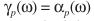，可以得到类似的降噪算法

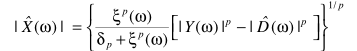
其中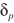是与p有关的常数，如对应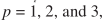。得到估计之后可以通过上面提到一些方式作进一步的后处理。

这个方法的关键在于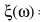：作为一个理论值，实际应用如何估计它？

直观的思路是，可以借助已处理的信息进行估计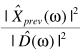：，也可以利用当前信息估计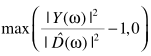：，一种折中的思路是二者的权衡：

　　E-扩展谱减法

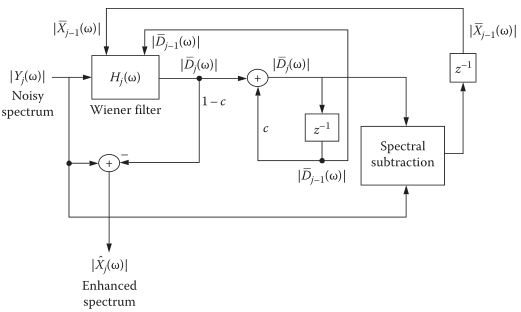
 上面的算法都需要借助VAD技术/噪声估计技术，实际上 维纳+谱减 的结合，可以实现降噪并称该方法：扩展谱减法。

维纳滤波原理

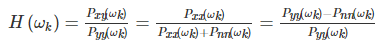
其中y为带噪信号，x为clean,n为noise.对于也就是

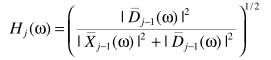
细节处理上可以用一下平滑

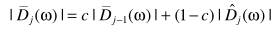
利用估计的噪声谱得出当前的噪声谱

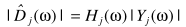
从而估计当前的信号

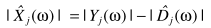
它是自适应的，不需要估计噪声，因此对于非平稳噪声环境也同样适用。实现框图：