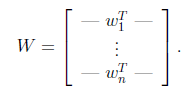独立成分分析(Independent component analysis, ICA)
作者:桂。
时间:2017-05-22 12:12:43
链接:http://www.cnblogs.com/xingshansi/p/6884273.html

前言
今天群里冒出这样一个问题:群里谁有INFORMAX语音分离源程序?看到要程序的就头大,这是一个盲源分离问题,之前没有推导过,借此过一遍思路。
一、问题描述
经典的鸡尾酒宴会问题(cocktail party problem)。假设在party中有n个人,他们可以同时说话,我们也在房间中一些角落里共放置了n个声音接收器(Microphone)用来记录声音。宴会过后,我们从n个麦克风中得到了一组数据![]() ,i表示采样的时间顺序,也就是说共得到了m组采样,每一组采样都是n维的。我们的目标是单单从这m组采样数据中分辨出每个人说话的信号。
,i表示采样的时间顺序,也就是说共得到了m组采样,每一组采样都是n维的。我们的目标是单单从这m组采样数据中分辨出每个人说话的信号。
将第二个问题细化一下,有n个信号源![]() ,
,![]() ,每一维都是一个人的声音信号,每个人发出的声音信号独立。A是一个未知的混合矩阵(mixing matrix),用来组合叠加信号s,那么
,每一维都是一个人的声音信号,每个人发出的声音信号独立。A是一个未知的混合矩阵(mixing matrix),用来组合叠加信号s,那么
x的意义在上文解释过,这里的x不是一个向量,是一个矩阵。其中每个列向量是![]() ,
,![]() ,表示成图就是:
,表示成图就是:

![]() 的每个分量都由
的每个分量都由![]() 的分量线性表示。A和s都是未知的,x是已知的,我们要想办法根据x来推出s。这个过程也称作为盲信号分离。
的分量线性表示。A和s都是未知的,x是已知的,我们要想办法根据x来推出s。这个过程也称作为盲信号分离。
将W表示成
ICA的主要任务是估计解混矩阵W。
二、理论求解(不感兴趣可跳过)
A-理论基础
标准ICA理论有几个支撑点:
1)各源信号统计独立;
2)至多有一个源信号服从Gauss分布
对于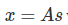 ,并假设
,并假设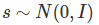 ,则有:
,则有:
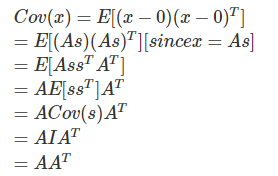
另一方面,对于任意正交矩阵: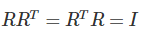 ,令
,令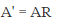 :
:
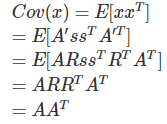
可见混合矩阵无法有效估计。
3)混合矩阵为方阵
B-理论求解
1-中心极限定理:
中心极限定理表明:对于混合信号,其概率密度比任何一个源信号的概率分布都接近高斯分布;反过来,最大化信号的非高斯性与最大化信号的统计独立性是一致的,只是ICA的基本原理。
2-非高斯性度量
a)利用统计量
峭度(kurtosis)
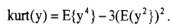
峭度基本性质:

b)利用信息论知识
熵的定义:
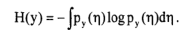
负熵:

给出基于KL散度的定义:

互信息:
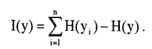
考虑负熵的定义,上式重写为:
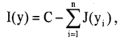
该式表明:最小化互信息等价于最大化负熵。
对于负熵,有时为了简化常用近似的方法:
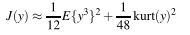
上面的逼近通常不够理想,改进版的近似:
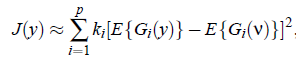
其中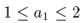 ,且:
,且:
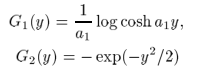
c)利用概率估计
利用MLE准则进行参数估计。
三、算法实现
给出利用概率估计的算法原理,准则函数(取对数):
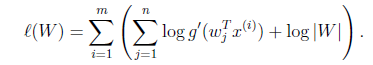
其中: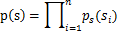 ,从而
,从而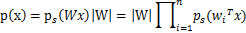 。这里的g表示概率密度,可以用sigmoid函数,也可以用tan函数等等,以sigmoid函数为例:
。这里的g表示概率密度,可以用sigmoid函数,也可以用tan函数等等,以sigmoid函数为例:
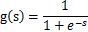
由于: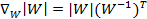 ,利用梯度下降法求解。给出梯度的计算公式:
,利用梯度下降法求解。给出梯度的计算公式:
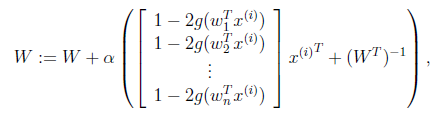 给出主要code实现:
给出主要code实现:
for iter=1:length(anneal)
iter
% Randomly interate through the samples running stochastic gradient descent
rowIndices = randperm(m);
for i = 1:length(rowIndices)
rowIndex = rowIndices(i);
% Perform the ICA stochastic gradient descent update
W = W + anneal(iter) * ((ones(n,1)-2*ones(n,1)./(ones(n,1)+exp(-W*mix(rowIndex,:)')))*mix(rowIndex,:) + (W')^-1);
end
end;
四、其他
A-ICA的不确定性
1-分离信号幅度与初始相位的不确定性
信源信号S和混合矩阵A:
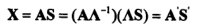
可以看出,对于实数信号产生幅度不确定性,对于复数信号,产生幅度与相位的不确定性。
幅度的不确定性可以采用假设信号单位方差的方法修正。
2-分离信号的次序不确定性
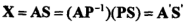
P是任意置换矩阵,这就造成了分离信号次序的不确定性。
B-ICA中的预处理
1-中心化
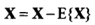
ICA算法中,均值为零可以使得很多相乘项为零,简化算法复杂性。
2-白化处理
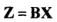
B为白化矩阵。白化操作之前有介绍,白化处理已经包含了中心化。ICA中的白化通常指满秩的白化。
白化的本质就是旋转+方差单位化。白化操作是去除信号的相关性,以基于信息论的ICA为例,各个概率密度独立是理论假设的基本前提。
参考

- http://www.cnblogs.com/jerrylead/archive/2011/04/19/2021071.html