统计学习方法:支撑向量机(SVM)
作者:桂。
时间:2017-05-13 21:52:14
链接:http://www.cnblogs.com/xingshansi/p/6850684.html

前言
主要记录SVM的相关知识,参考的是李航的《统计学习方法》,最后的SMO优化算法(Sequential minimal optimization)是二次规划的优化算法,不涉及整体思路的理解,这里打算跳过,以后用到了再来回顾。
一、线性可分支撑向量机
A-问题分析
不同于感知器Perceptron,SVM希望所有点到分离面的最小距离最大化,而距离分离面最近的样本点就是支撑向量(support vector):

样本点到分离面的距离:

定义最小间隔:
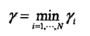
最小间隔最大化就是如下的优化问题:
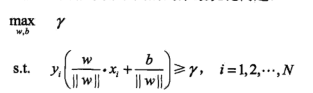
令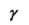 =
=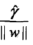 ,则优化问题改写为:
,则优化问题改写为:
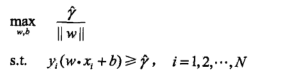
事实上 的取值不影响最终的最优解,进一步转化优化问题:
的取值不影响最终的最优解,进一步转化优化问题:

这就成了一个凸二次规划(convex quadratic programming)问题了,满足凸优化的形式,可以借助对偶简化求解。
引进拉格朗日乘子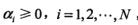 :
:

原始问题为极小极大问题,转化问对偶就是极大极小问题:
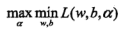
先极小求解,上述优化问题可以简化为:
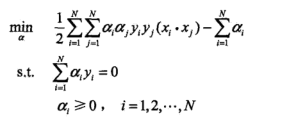
根据KKT条件,上述解对应原问题的解:
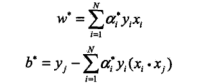
从而完成求解。
B-算法步骤
C-应用举例
只不过这里不是求解感知器,而是SVM。
第一步:对偶问题求解
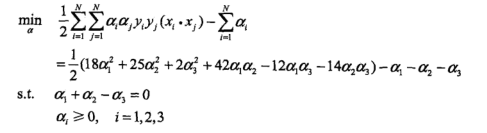 求出的最优解(a1,a2)是
求出的最优解(a1,a2)是 ,但a2 = -1不满足约束a2>=0,所以最小值在边界取得。
,但a2 = -1不满足约束a2>=0,所以最小值在边界取得。
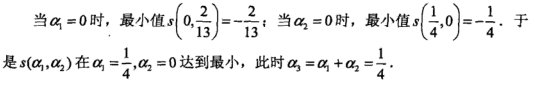
第二步:计算w与b
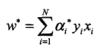 =1/4*[3, 3]*1+1/4*[1, 1]*(-1)=[1/2, 1/2]
=1/4*[3, 3]*1+1/4*[1, 1]*(-1)=[1/2, 1/2]
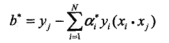 =-2
=-2
第三步:得出分离决策面
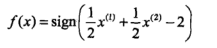
二、线性不可分情况
A-问题分析
其实它是对线性可分的推广,对线性可分的情况仍然适用。对于线性不可分的解决办法就是引入松弛变量,也就是加入了误差扰动:

引入松弛变量优化时考虑两方面:1)最小距离尽可能大; 2)误分类点个数尽量小。得出新的准则函数:

仍然借助对偶问题求解(剩下的思路与线性可分问题的求解思路完全一致):
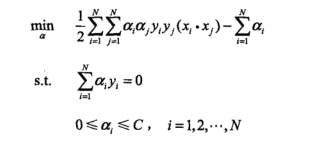
进一步得到原始问题的解:
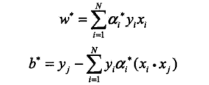
从而完成求解。
B-准则函数补充
因为超平面都是可以伸缩的,假设全部正确分类:
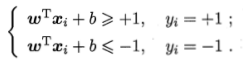
最小间隔:
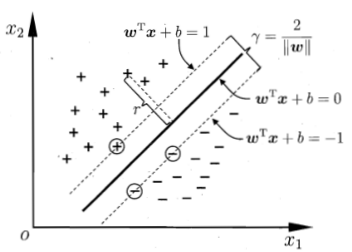
这是硬间隔,但实际中可能不能完全线性分开:
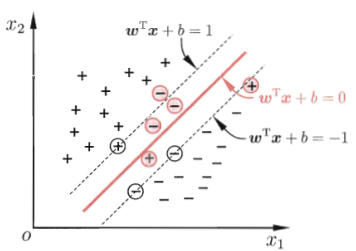
这个时候就是软间隔,即允许部分数据不满足:
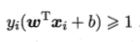
当然最大化间隔时,希望不满足条件的样本点数尽可能小,给出准则函数:

其中 是0/1损失函数,用来定义不满足条件的样本数:
是0/1损失函数,用来定义不满足条件的样本数:
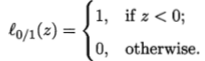
但是 非凸、非连续,可以近似替代处理:
非凸、非连续,可以近似替代处理:
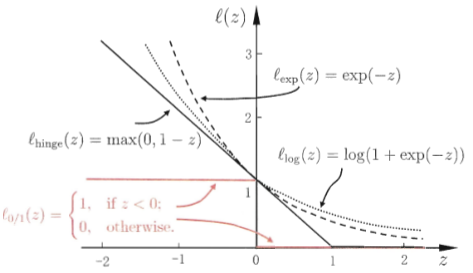
常用替代方式有三类:
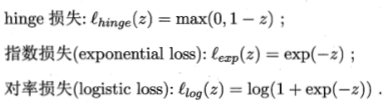
如果采用hinge损失,损失函数转化为:
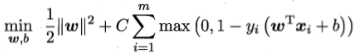
将 定义为松弛变量
定义为松弛变量 ,上式等价为:
,上式等价为:
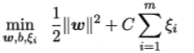
这个就是线性不可分时的准则函数了。最后回头看看近似与 之间的关系:
之间的关系:
C-算法步骤
给出线性支撑向量机学习算法:
三、非线性情况
关于核函数的应用,之前的文章已经分析过。
什么样的函数可以作为核函数?充要条件——K(x,z)为正定核函数:
考虑矩阵的特征值。
若所有特征值均不小于零,则称为半正定。
若所有特征值均大于零,则称为正定。
参考:
- 李航《统计学习方法》







