矩阵白化
作者:桂。
时间:2017-04-11 22:08:55
链接:http://www.cnblogs.com/xingshansi/p/6696793.html
声明:欢迎被转载,不过记得注明出处哦~

前言
在子空间分析、独立成分分析等应用中,经常用到矩阵白化,这里简单总结一下,主要包括:
1)满秩矩阵的白化;
2)秩亏缺矩阵的白化;
3)白化与PCA的关系;
内容为自己的学习记录,其中多有借鉴他人之处,最后一并给出链接。
一、满秩矩阵的白化
令![]() 是随机向量,零均值,其协方差矩阵:
是随机向量,零均值,其协方差矩阵:
![]()
如果协方差矩阵非奇异,对其特征值分解(特征值及SVD的细节信息,前文有介绍):
![]()
定义矩阵:
![]()
$\bf{W}$成为$\bf{a}$的白化矩阵。白化后的信号:
![]()
其协方差矩阵等于单位阵。
总结一下步骤:
步骤一:去均值,中心化
步骤二:求协方差矩阵,并进行特征值分解
步骤三:求解白化矩阵,并得到白化后的信号
给出一段示意代码:
x = -10:.1:10; x = x +randn(1,length(x)); y = 0.6*x + randn(1,length(x)); %whiten data = [x;y]; C = data*data'; [u,s,v] = svd(C); W = v*diag(1./sqrt(diag(s)))*v'; b = W*data;
对应结果:
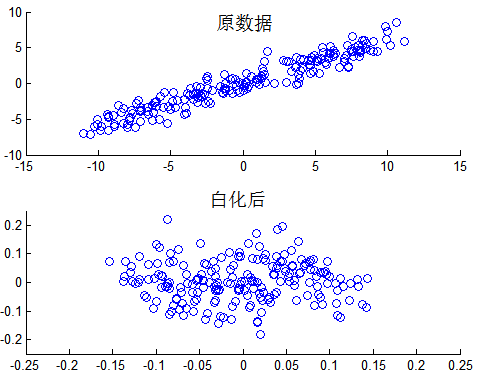
可见白化其实就是让信号尽可能不相关。在分析PCA的时候,我们知道特征值与对应方向的方差有关联,所以白化就是这个思路:首先旋转坐标轴,其次根据对应方向的方差(特征值)进行伸缩,中心化的目的就是为了保证变换前后数据中心对应坐标轴中心,而不至于因为旋转/伸缩而偏离坐标原点太过分:
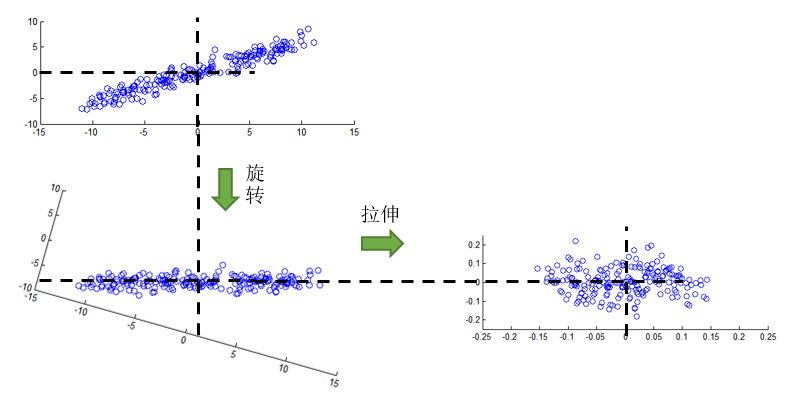
是不是觉得与PCA相像?后面给出分析。
二、秩亏缺矩阵的白化
当协方差矩阵为秩亏缺时,可以写为:
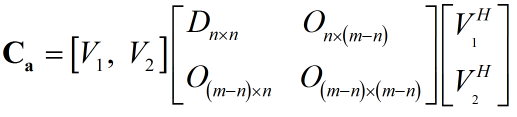
此时白化矩阵为:
![]()
白化后的信号:
![]()
此时白化后信号的协方差矩阵:
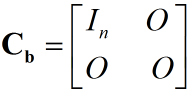
至此,完成白化。这也容易理解,有效信号占一个子空间,对子空间白化,就是对有效信号进行白化。
三、白化与PCA
PCA前文有分析,给出PCA步骤:
步骤一:数据中心化——去均值;
步骤二:求解协方差矩阵;
步骤三:利用特征值分解/奇异值分解 求解特征值以及特征向量;
步骤四:利用特征向量构造投影矩阵;
步骤五:利用投影矩阵,得出降维的数据。
以上文二维数据为例:
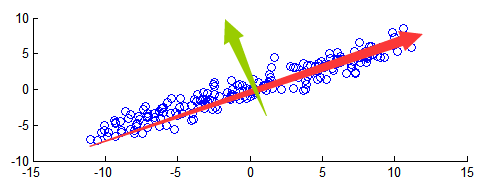
- 中心化:白化的中心化,PCA也需要中心化;
- 旋转:白化步骤中的旋转,即旋转后的坐标就是PCA对应的第一、第二投影方向,如图中红线、绿线所示;
- 拉伸:不同维度的特征值通常差别较大,在PCA中就是对特征值进行归一化。如果将不同维度的数据看作不同特征,白化步骤的拉伸本质也是特征的归一化。
参考:
张贤达:《矩阵分析与应用》


