自适应滤波:递归最小二乘
作者:桂。
时间:2017-04-04 15:51:03
链接:http://www.cnblogs.com/xingshansi/p/6664478.html
声明:欢迎被转载,不过记得注明出处哦~

【读书笔记12】
前言
西蒙.赫金的《自适应滤波器原理》第四版第九章:递归最小二乘(Recursive least squares, RLS)。记得看完第一章之后,半个月没有碰这本书,后来想着开了个头,还是该看到第十章的卡尔曼滤波才好,前前后后又花了半个月,总算看到了第九章。回头看看,静下心来,确实容易理清思路,也学到不少知识。虽然前路漫漫,编程水平不够、机器学习的理论还没多少概念、算法基础没多少、收入也很微薄......不过还是该表扬一下自己。既然选择了道路,自己还是该耐心走下去,哪怕上不了山顶,也该看看高处的风景。
言归正传,本文主要包括:
1)RLS原理介绍;
2)RLS应用实例;
内容为自己的学习记录,其中多有借鉴他人的地方,最后一并给出链接。
一、RLS原理介绍
A-问题描述
考虑指数加权的优化问题:
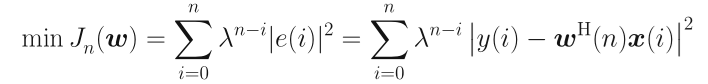
为遗忘因子,这里只讨论平稳情况,取。
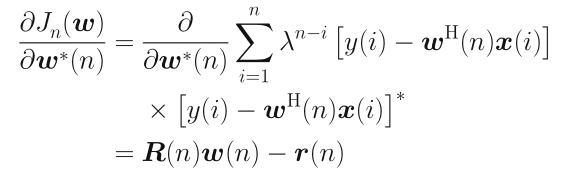
从而得到最优解:
![]()
其中:
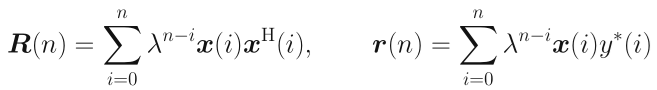
可以看到,对应的就是最小二乘思想。回头看看之前分析的LMS以及NLMS,用的是随机梯度下降的思想,这是RLS与LMS很明显的不同点。
由于、时刻在变换,最优解如何更新呢?
B-迭代更新
首先给出文中用到的矩阵求逆引理:
矩阵求逆引理:
定义逆矩阵:
![]()
利用矩阵求逆引理:
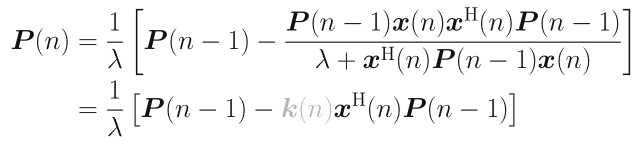
其中称为增益向量,由上式得出:
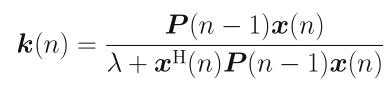
借助迭代:
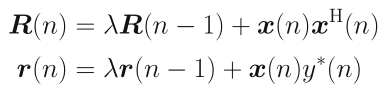
可以得到权重的更新公式:
![]()
其中![]() 为估计误差:
为估计误差:
![]()
至此实现RLS的整个步骤。
二、RLS应用实例
A-算法步骤
结合上文的推导,给出RLS的迭代步骤:
步骤一:初始化
其中为很小的正数,如1e-7;
步骤二:迭代更新
B-代码应用
给出主要代码,可以结合前文的LMS/NLMS对比分析:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | function [e,w]=rls(lambda,M,u,d,delta)% recursive least squares,rls.% Call:% [e,w]=rls(lambda,M,u,d,delta)%% Input arguments:% lambda = constant, (0,1]% M = filter length, dim 1x1% u = input signal, dim Nx1% d = desired signal, dim Nx1% delta = constant for initializaton, suggest 1e-7.%% Output arguments:% e = estimation error, dim Nx1% w = final filter coefficients, dim Mx1% Step1:initialize% 2017-4-4 14:34:33, Author: Guiw=zeros(M,1);P=eye(M)/delta;u=u(:);d=d(:);% input signal lengthN=length(u);% error vectore=d.';% Step2: Loop, RLSfor n=M:N uvec=u(n:-1:n-M+1); e(n)=d(n)-w'*uvec; k=lambda^(-1)*P*uvec/(1+lambda^(-1)*uvec'*P*uvec); P=lambda^(-1)*P-lambda^(-1)*k*uvec'*P; w=w+k*conj(e(n));end |
给出应用:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | [s, fs, bits] = wavread(filename); s=s-mean(s); s=s/max(abs(s)); N=length(s); time=(0:N-1)/fs; clean=s';ref_noise=.1*randn(1,length(s));mixed = clean+ref_noise;mu=0.05;M=2;espon=1e-4;% [en,wn,yn]=lmsFunc(mu,M,ref_noise,mixed);% [en,wn,yn]=nlmsFunc(mu,M,ref_noise,mixed,espon);delta = 1e-7;lambda = 1;[en,w]=rls(lambda,M,ref_noise,mixed,delta); |
对应结果图:
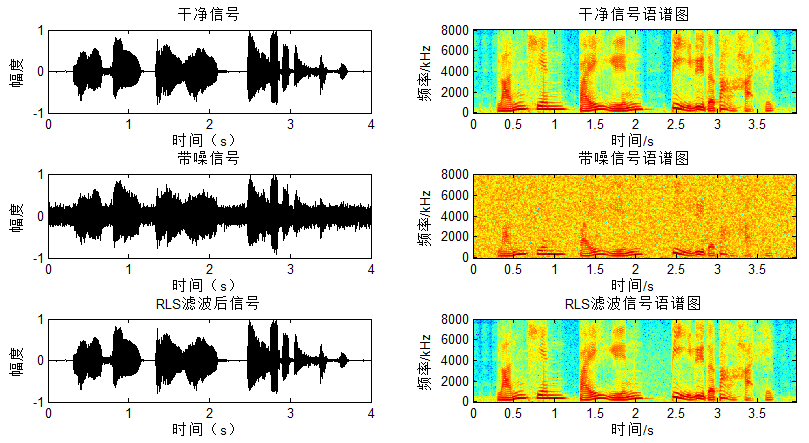
可以看出不像NLMS/LMS有一个慢速收敛的过程,RLS在开始阶段就得到较好的降噪。
C-与LMS对比
与LMS对比,可以观察到RLS的几点特性:
- 平稳环境λ=1,其实是最小二乘的思想;LMS/NLMS是随机梯度下降思想;
- 最小二乘是直接得出结果,随机梯度下降收敛慢,因此RLS比LMS/NLMS收敛快一个数量级;
参考:
- Simon Haykin 《Adaptive Filter Theory Fourth Edition》.



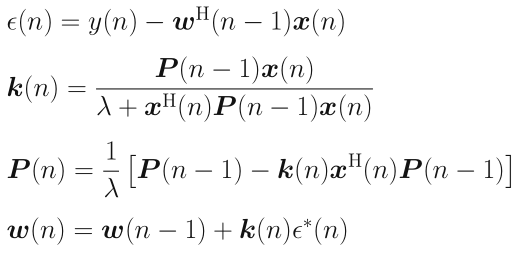


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 字符编码:从基础到乱码解决