数据量化与频域分析

作者：桂。

时间：2017-03-24  18:46:24

链接：http://www.cnblogs.com/xingshansi/p/6612973.html 

声明：欢迎被转载，不过记得注明出处哦~

---

 

前言

本文的应用背景是：对序列信号进行频域变换，从而估计频率。但在信号处理中，通常需要对数据进行量化，以此减少量化位数从而减少数据量，另外在进行频域变换时，对频域的旋转矩阵进行量化，同样可以减少数据量。本文对应的专业术语：MonoDFT、单比特。全文主要分为：

　　1）数据的量化；

　　2）傅里叶旋转矩阵量化；

之前朋友问我这个问题，觉得也算一种减少数据运算量的粗糙方式，记录在此。

 

一、数据的量化

对采样的数据进行量化，量化位数可以根据需求选定，正常数据量过大的话对于高频采样难以保证精度，此处以单比特为例。即$s_{quan} = sign(s)$。

以采样率为$40Hz$为例，频率为8的信号，对比采样信号与单比特量化后的信号：

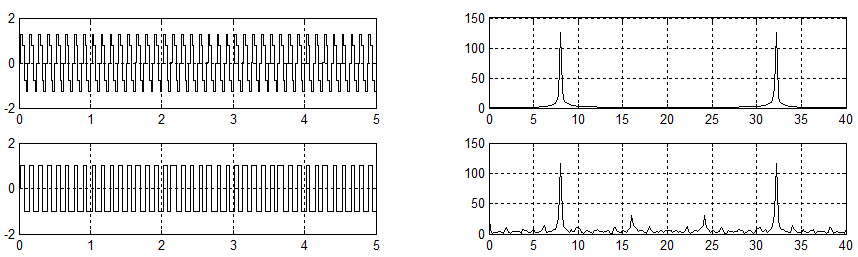
可以看出尽管由于单比特后信号成方波状，引入谐波分量误差以及其他频率的杂波，但如果仅仅为了测频——找到峰值点，则仍然是有效的。

 

二、旋转矩阵的量化

该测频方法有专业术语：MonoDFT.

即对矩阵W进行量化：

其实W对应在频率圆周上采样：

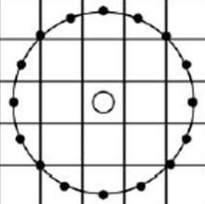
量化以后可以简化运算（比如只用加减），具体不详细讨论，给出量化示意图，以W量化成4个不同取值为例：

以8HZ信号进行频率估计：

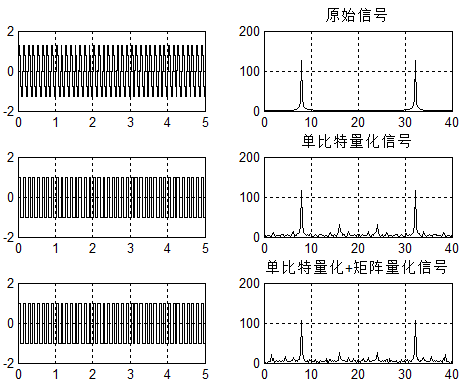
可以看出虽然引入误差，但在信噪比合适的情况下，处理后的数据完全足以估计信号频率。

但由于误差的引入，只能对单个信号较为有效，以两个为例：

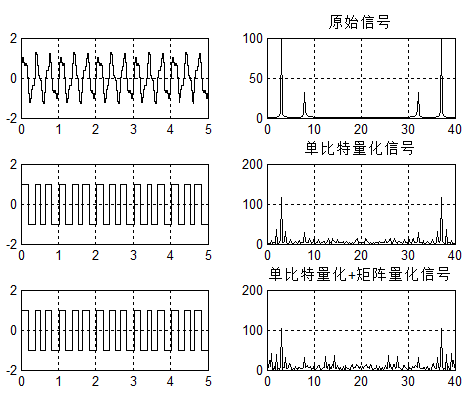
这是两个信号，但第二个频率分量已经淹没在噪声中。

给出代码：

clc;clear all;close all;
set(0,'defaultfigurecolor','w');
fs = 40;
f1 = 8;
f2 = 3;
t_end = 5;
t = 0:1/fs:t_end;
s1 = 0.35*sin(2*pi*f1*t);
s2 = sin(2*pi*f2*t);
s = s1+s2;
f = t/max(t)*fs;
N = length(t);
%====原数据-DFT
W = exp(-j*2*pi/N).^([0:N-1]'*[0:N-1]);
Sori = W*s';
%====单比特-DFT
s1 = sign(s);
Sori1 = W*s1';
%====单比特+旋转因子量化
flag1 = real(W)>imag(W);
flag2 = real(W)>(-imag(W));
W1 = flag1.*flag2;
W2 = 1j*(~flag1).*flag2;
W3 = -(~flag1).*(~flag2);
W4 = -1j*flag1.*(~flag2);
Wnew = W1+W2+W3+W4;
Sori2 = Wnew*s1';
%====figure
figure;
subplot 321
stairs(t,s,'k');grid on;
xlim([0,t_end]);
ylim([-2,2]);
subplot 322
plot(f,abs(Sori),'k');grid on;title('原始信号');
subplot 323
stairs(t,s1,'k');grid on;
xlim([0,t_end]);
ylim([-2,2]);
subplot 324
plot(f,abs(Sori1),'k');grid on;title('单比特量化信号');
subplot 325
stairs(t,s1,'k');grid on;
xlim([0,t_end]);
ylim([-2,2]);
subplot 326
plot(f,abs(Sori2),'k');grid on;title('单比特量化+矩阵量化信号');