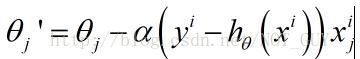关于梯度下降

 

梯度下降法是一个最优化算法，通常也称为最速下降法。最速下降法是求解无约束优化问题最简单和最古老的方法之一，虽然现在已经不具有实用性，但是许多有效算法都是以它为基础进行改进和修正而得到的。最速下降法是用负梯度方向为搜索方向的，最速下降法越接近目标值，步长越小，前进越慢。

梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。

 

 

最小二乘问题(least square problem)亦称最小平差问题.数值逼近的重要问题之一是用离散平 　　方逼近技术求拟合曲线的问题.设已知节点组x1 CxzC...Cxm上相应的实验值为.f},.fz,...,.fm.最小二乘问题是指，在已取定的某函数类中，求目标函数F (.x)使其方差，即各样点处偏差的平方和

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳 函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于 曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

 

以下为博客转载

样本个数为m，x为n维的向量。

 

（1）

批量梯度下降：

权值更新公式：

 

 

从公式中可以看出，批量梯度下降算法每迭代一步，要用到训练集的所有样本，最后得到的是一个全局最优解。

 

（2）随机梯度下降：

权值更新公式：

 

也是看公式，能够发现随机梯度的权值更新公式里调整项没有累加符号，说明随机梯度下降中只用到了训练集的一个样本，最后得到的可能是全局最优解，也可能是局部最优解。
---------------------
作者：__gyl__
来源：CSDN
原文：https://blog.csdn.net/NOT_GUY/article/details/73866478
版权声明：本文为博主原创文章，转载请附上博文链接！