CSP-S考前各种idea题解乱堆
快要考试了我还是这么菜。
已经没有心思维护我的博客了。开一篇博文吧。可能会记得很乱。
这也许是我OI生涯的最后一篇博文了??
肯定很长很长。
不可能的。谁知道什么时候我心态恢复就把上面两句话删掉开始在博客里各种胡咧咧了。
好,我心态恢复了。我要写日记了hhh
「$idea$」维护凸包
临考前才学必定致命。
主要因为昨天考了一套题,T1是凸包。%%%$OOO$李超线段树怒切T1。
我要澄清一下,关于$OOO$大神在李超线段树的学习笔记中提到本人,
本人对此严正声明:我不会李超线段树。我只是颓废,大神一直在学习。
至于他会不会发布这篇笔记我不清楚。
上面是废话
凸包其实是个非常简单的东西。之前一直觉得特别难。
其实之前有一次临时决定强行学习一波,打开一个学习笔记,第一眼:叉积。
告辞。
然后发现,其实只需要对斜率排个序,求个交点,单队或者单调栈维护一下就行了。
「$idea$」树的遍历
谁也不知道我为什么突然脑抽去看树的遍历。。。
实际上并没有什么用处。。。
放个链接:树的遍历
「题解」笨小猴:结论题
赛时$random\_shuffle$本来能$AC$。
结果统计总和没开$long$ $long$,$OJ$测拿了$20$,$lemon$测拿了50。
$lemon$测比$OJ$测高也是创了个记录。
简要题解:
把所有卡片按照$A$的大小排序。然后从左到右每两张卡片分成一组,我们选取每组中$B$较大的,再将最后一张卡片选取即可。
证明:最坏的情况无非两两一组中总是$A$较小的那个$B$较大。此时我们换一种分组方式,把$1$提出来,$2,3$一组,以此类推就全是$A$较大的那个$B$较大了。
所以没有$-1$情况。
代码:
这个是$random\_shuffle$的。
#include<bits/stdc++.h>
#define int long long
#define rint register int
using namespace std;
inline void read(int &a)
{
a=0;int b=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,a[200005],b[200005],Suma,Sumb,ans[100005],tim,id[200005];
inline void dfs(int k,int gt,int suma,int sumb)
{
if(gt==n+1)
{
if(suma>Suma-suma&&sumb>Sumb-sumb)
{
for(rint i=1;i<=gt;++i)
printf("%d\n",ans[i]);
exit(0);
}
return ;
}
if(k==2*n+2)return ;
dfs(k+1,gt,suma,sumb);ans[gt+1]=k;
dfs(k+1,gt+1,suma+a[k],sumb+b[k]);
return ;
}
signed main()
{
freopen("grandmaster.in","r",stdin);
freopen("grandmaster.out","w",stdout);
srand(time(NULL));
tim=clock();read(n);
for(rint i=1;i<=2*n+1;++i)
{
read(a[i]),read(b[i]);
Suma+=a[i],Sumb+=b[i],id[i]=i;
}
if(n<=10){dfs(1,0,0,0);puts("-1");return 0;}
while(1)
{
if(clock()-tim>940000)break;
random_shuffle(id+1,id+2*n+1);
int sa=0,sb=0;
for(rint i=1;i<=n+1;++i)
sa+=a[id[i]],sb+=b[id[i]];
if(sa>Suma-sa&&sb>Sumb-sb)
{
for(rint i=1;i<=n+1;++i)
printf("%d\n",id[i]);
return 0;
}
}
puts("-1");return 0;
}
这个是正解。
#include<bits/stdc++.h>
#define rint register int
using namespace std;
inline void read(int &a)
{
a=0;int b=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,ans[100005],tim,id[200005];
struct node{int a,b,id;}pi[200005];
inline bool cmp(node A,node B){return A.a<B.a;}
int main()
{
freopen("grandmaster.in","r",stdin);
freopen("grandmaster.out","w",stdout);
read(n);
for(rint i=1;i<=2*n+1;++i)
read(pi[i].a),read(pi[i].b),pi[i].id=i;
sort(pi+1,pi+2*n+1+1,cmp);
for(rint i=1;i<=n;++i)
{
if(pi[(i<<1)-1].b<=pi[i<<1].b)
printf("%d\n",pi[i<<1].id);
else printf("%d\n",pi[(i<<1)-1].id);
}
printf("%d\n",pi[2*n+1].id);
return 0;
}
「题解」开心的金明:贪心+模拟
我没看出来这道题和金明有半毛钱关系。。。办公司的不是小木么。。。
简要题解:
贪心。不想证明。
电脑能造多少造多少,大不了不卖都扔掉。卖电脑的时候选成本最小的卖掉,成本大的可以退掉。
然后就没了。维护两个小根堆来回捯完事了。
注意别一个电脑一个电脑的模拟,会T60。一组一组得处理。
代码:
#include<bits/stdc++.h>
#define int long long
#define rint register int
using namespace std;
const int N=50004,inf=0x7fffffff;
inline void read(int &a)
{
a=0;int b=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,ci[N],di[N],pi[N],mi[N],ei[N],ri[N],gi[N];
int yt[N],ccf[N],ycb[N],ck[N],now,sum,ans;
struct node{int wi,num;};
bool operator < (node A,node B){
return A.wi>B.wi;
}
priority_queue<node> q[2];
signed main()
{
freopen("happy.in","r",stdin);
freopen("happy.out","w",stdout);
read(n);ci[0]=inf;memset(ycb,0x7f,sizeof(ycb));
for(rint i=1;i<=n;++i)read(ci[i]),read(di[i]),read(mi[i]),read(pi[i]);
for(rint i=1;i<n;++i)read(ei[i]),read(ri[i]),read(gi[i]),ccf[i+1]=ccf[i]+ri[i];
for(rint i=1;i<=n;++i)
{
if(ci[yt[i-1]]+ccf[i]-ccf[yt[i-1]]<ycb[i])
ycb[i]=ci[yt[i-1]]+ccf[i]-ccf[yt[i-1]],yt[i]=yt[i-1];
if(ci[i]<ycb[i])yt[i]=i,ycb[i]=ci[i];
}
for(rint i=1;i<=n;++i,now^=1)
{
if(sum+pi[i]<di[i])return puts("-1"),0;
q[now].push((node){ycb[i]+mi[i],pi[i]});
int lin=0;
while(lin+q[now].top().num<=di[i])
ans+=q[now].top().num*q[now].top().wi,lin+=q[now].top().num,q[now].pop();
if(lin<di[i])
{
int dwi=q[now].top().wi,dnum=q[now].top().num,lst=di[i]-lin;
ans+=lst*dwi;q[now].pop();q[now].push((node){dwi,dnum-lst});
}
while(q[!now].size())q[!now].pop();
lin=sum=0;
while((!q[now].empty())&&lin+q[now].top().num<=ei[i])
{
q[!now].push((node){q[now].top().wi+gi[i],q[now].top().num});
lin+=q[now].top().num,sum+=q[now].top().num,q[now].pop();
}
if(lin<ei[i]&&(!q[now].empty()))
{
int dwi=q[now].top().wi,dnum=q[now].top().num,lst=ei[i]-lin;
q[!now].push((node){dwi+gi[i],lst});sum+=lst;
}
}
printf("%lld\n",ans);
return 0;
}
「题解」陶陶摘苹果:线段树+二分+单调栈
我们熟悉陶陶摘苹果,苹果摘陶陶,这次陶陶再次来摘苹果了,是排序还是贪心,是迪利克雷卷积还是快速傅里叶变换。
我说我没看出来线段树维护单调栈你信么。。。考场上自己yy了一个$O(nlog^2n)$的做法。
简要题解:
可以发现,对于一个位置的改变,最终答案可以拆成两部分:该位置前的和该位置后的。
我们可以考虑先在原本的序列上跑一遍答案,记录下来答案路径,然后用线段树记录区间最大值和区间最大值第一次出现的位置,还要跑一遍单调栈维护出所有节点到最后的上升序列长度。
对于这个位置以前的部分,有一个显然的性质是这一部分的区间最大值第一次出现的位置一定在答案路径上。
我更改的是它后面的值,不会对它的答案路径产生影响。所以直接继承过来到它的答案路径长度。
如果我当前更改的值要大于前一部分的最大值,则当前节点也在本次更改的答案路径上。ans++,区间最大值要更新为当前修改值。
对于后一部分,二分找到第一个比当前值要大的值的位置,答案加上这个位置到最后的上升序列长度即可。
代码:
#include<bits/stdc++.h>
#define rint register int
using namespace std;
const int inf=0x7fffffff;
inline void read(int &a)
{
a=0;int b=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,m,h[100005];
int t[100005<<5],loc[100005<<5];
int sta[100005],tp,bop[100005],len[100005];
int ky[100005],rd[100005],cnt;
inline void update(int k)
{
t[k]=max(t[k<<1],t[k<<1|1]);
if(t[k]==t[k<<1])loc[k]=loc[k<<1];
else loc[k]=loc[k<<1|1];
}
inline void build(int k,int l,int r)
{
if(l==r){t[k]=h[l],loc[k]=l;return ;}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
update(k);return ;
}
inline void change(int k,int l,int r,int p,int dat)
{
if(l==r){t[k]=dat;return ;}
int mid=(l+r)>>1;
if(p<=mid)change(k<<1,l,mid,p,dat);
else change(k<<1|1,mid+1,r,p,dat);
update(k);return ;
}
inline void query(int k,int l,int r,int L,int R,int &res,int &lc)
{
if(R<L)return res=0,lc=0,void();
if(L<=l&&r<=R){if(t[k]>res)res=t[k],lc=loc[k];return ;}
int mid=(l+r)>>1;
if(L<=mid)query(k<<1,l,mid,L,R,res,lc);
if(R>mid)query(k<<1|1,mid+1,r,L,R,res,lc);
return ;
}
inline int ef(int st,int dat)
{
int l=st,r=n+1;
while(l<r)
{
int mid=(l+r)>>1,res=0,lc=0;
query(1,1,n,st,mid,res,lc);
if(res<=dat)l=mid+1;
else r=mid;
}
return len[l];
}
int main()
{
freopen("TaoPApp.in","r",stdin);
freopen("TaoPApp.out","w",stdout);
read(n),read(m);h[0]=inf;
for(rint i=1;i<=n;++i)read(h[i]);
if(n<=5000&&m<=5000)
{
for(rint i=1,p,hp,tp,lin,ans;i<=m;++i)
{
read(p),read(hp);tp=h[p],h[p]=hp;
lin=ans=0;
for(rint j=1;j<=n;++j)
if(h[j]>lin)lin=h[j],ans++;
printf("%d\n",ans);h[p]=tp;
}
return 0;
}
build(1,1,n);
for(rint i=1;i<=n;++i)
{
while(h[sta[tp]]<h[i])bop[sta[tp--]]=i;
sta[++tp]=i;
}
for(rint i=n;i>=1;--i)len[i]=len[bop[i]]+1;
int mxp=0;
for(rint i=1;i<=n;++i)
if(h[i]>mxp)mxp=h[i],rd[++cnt]=i,ky[i]=cnt;
for(rint i=1,p,hp,ans;i<=m;++i)
{
read(p),read(hp);ans=0;
int res=0,lc=0,tag=hp;
query(1,1,n,1,p-1,res,lc);
ans=ky[lc];
(res>=hp)?tag=res:ans++;
ans+=ef(p+1,tag);
printf("%d\n",ans);
}
return 0;
}
「题解」求和:等差数列求和公式
$sb$等差数列求和公式,取模后再除以2挂了$70$分神白名列。
改了半天没改过,请$Wang\_hecao$大佬帮我$debug$了一下。
还有C承担两次除法这种操作??
简要题解:
$sb$等差数列求和公式。
取模后不能做除法运算。取模后不能做除法运算。取模后不能做除法运算。
代码:
#include<bits/stdc++.h>
#define int long long
#define rint register int
using namespace std;
inline void read(int &a)
{
a=0;int b=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int l,u,r,d,mod,A,B,C,ans,flag=0;
inline int qpow(int a,int b)
{
int sum=1;
while(b){if(b&1)sum=sum*a%mod;a=a*a%mod;b>>=1;}
return sum;
}
inline int multi(int a,int b)
{
int sum=0;
while(b){if(b&1)sum=(sum+a)%mod;a=(a+a)%mod;b>>=1;}
return sum;
}
signed main()
{
freopen("sum.in","r",stdin);
freopen("sum.out","w",stdout);
read(l),read(u),read(r),read(d),read(mod);
A=r-l+1;B=d-u+1;C=l+u+r+d-2;
if(A%2==0)A/=2,flag++;
if(B%2==0&&!flag)B/=2,flag++;
if(C%2==0&&!flag)C/=2,flag++;
A%=mod;B%=mod;C%=mod;
ans=multi(multi(A,B),C)%mod;
printf("%lld\n",ans);
return 0;
}
「题解」分组配对:倍增+二分
赛时开了4个手写栈,最坏时间复杂度$O(n^2)$水了75分,一直觉得带上二分是$O(n^2log)$的结果人家有85-90的好成绩。。
感谢lyl大佬带我重新认识二分。这个世界上没有普适的二分板子.jpg。
简要题解:
倍增判定范围,二分确定具体分界点,可以保证时间复杂度稳定为$O(nlog^2n)$
代码:
#include<bits/stdc++.h>
#define int long long
#define rint register int
using namespace std;
inline void read(int &a)
{
a=0;int b=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,m,a[500005],b[500005],sum;
int male[500005],female[500005];
inline bool check(int lb,int rb)
{
int res=0;
for(rint i=lb;i<=rb;++i)male[i]=a[i],female[i]=b[i];
sort(male+lb,male+rb+1);sort(female+lb,female+rb+1);
for(rint i=lb;i<=rb;++i)res+=male[i]*female[i];
return res<m;
}
inline int work(int st,int l,int r)
{
while(l<r)
{
int mid=(l+r+1)>>1;
if(check(st,mid))l=mid;
else r=mid-1;
}
return l;
}
signed main()
{
freopen("pair.in","r",stdin);
freopen("pair.out","w",stdout);
read(n),read(m);
for(rint i=1;i<=n;++i)read(a[i]);
for(rint i=1;i<=n;++i)read(b[i]);
int st=1,en=1;
while(st<=n)
{
int pos=1;
for(;st+pos<n;pos<<=1)
if(!check(st,st+pos))break;
st=work(st,st+(pos>>1),min(st+pos,n))+1,sum++;
}
printf("%lld\n",sum);
return 0;
}
「题解」真相:预处理
赛时一直考虑如何正着推理然后就死了。
简要题解:
一个比较暴力的想法是枚举说「真」话的人数,枚举每一个意淫预言家,可以直接知道$ta$说的「真」$or$「假」,由此向上(逆时针)可以一直推到上一个预言家。
优化可以考虑直接预处理每个预言家到上一个预言家的区间,处理内容为当前预言家说话为「真」时区间内说真话的人数和当前预言家说话为「假」时区间内说真话的人数。然后按预言家的预言内容存储人数。由于同时最多只有一种预言家说的是真话,所以可以$O(1)$查询这种预言家说真话时说真话的人数,于是我们先自己预言所有预言家说的都是错的,直接统计所有预言家均说假话时说真话的人数,当查询每一种预言家的时候直接减去这种预言家说假话时说真话的人数,加上这种预言家说真话时说真话的人数即可。
代码:
#include<bits/stdc++.h>
#define rint register int
using namespace std;
inline void read(int &a)
{
a=0;int b=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int T,n,cnt[2][1000006],as[1000006];char ch[3];bool te=0;
vector <int> v;
struct node{int opt,wi;}h[1000006];
inline int lst(rint x){return (x==1)?n:x-1;}
int main()
{
freopen("truth.in","r",stdin);
freopen("truth.out","w",stdout);
read(T);
while(T--)
{
read(n);te=0;v.clear();
for(rint i=1;i<=n;++i)
{
scanf("%s",ch);
switch(ch[0])
{
case '+':h[i].opt=1;break;
case '-':h[i].opt=2;break;
case '$':
h[i].opt=3;read(h[i].wi);te=1;
v.push_back(i);break;
}
}
if(!te)
{
int tag=0;
for(rint i=1;i<=n;++i)
{
if(tag==0&&h[i].opt==1){tag=0;continue;}
if(tag==0&&h[i].opt==2){tag=1;continue;}
if(tag==1&&h[i].opt==1){tag=1;continue;}
if(tag==1&&h[i].opt==2){tag=0;continue;}
}
if(tag==0){puts("consistent");continue;}
else{puts("inconsistent");continue;}
}
else
{
for(rint i=0;i<=n;++i)cnt[0][i]=cnt[1][i]=0;
int ans=0;
for(rint j=0;j<v.size();++j)
{
int sum=0;
int lin=v[j],tag=0;
int loc=lin,lt=lst(lin);
while(h[lt].opt!=3)
{
if(tag==0&&h[lt].opt==1)tag=0;
else if(tag==0&&h[lt].opt==2)tag=1,sum++;
else if(tag==1&&h[lt].opt==1)tag=1,sum++;
else if(tag==1&&h[lt].opt==2)tag=0;
loc=lt,lt=lst(loc);
}
cnt[0][h[lin].wi]+=sum;
}
for(rint j=0;j<v.size();++j)
{
int sum=1;
int lin=v[j],tag=1;
int loc=lin,lt=lst(lin);
while(h[lt].opt!=3)
{
if(tag==0&&h[lt].opt==1)tag=0;
else if(tag==0&&h[lt].opt==2)tag=1,sum++;
else if(tag==1&&h[lt].opt==1)tag=1,sum++;
else if(tag==1&&h[lt].opt==2)tag=0;
loc=lt,lt=lst(loc);
}
cnt[1][h[lin].wi]+=sum;
}
for(rint i=0;i<=n;++i)ans+=cnt[0][i];
for(rint i=0;i<=n;++i)
{
ans-=cnt[0][i];ans+=cnt[1][i];
if(ans==i){puts("consistent");goto skyhecao;}
ans+=cnt[0][i];ans-=cnt[1][i];
}
puts("inconsistent");
skyhecao: continue;
}
}
}
/*
3
3
+
+
$ 3
3
+
-
$ 3
1
-
*/
「题解」格式化:排序题、贪心
简要题解:
所以我不会做排序题。赛时xjb写了三个排序加上$random_shuffle$水到了80分hhh。
正解排序方式:分个类,先格式化有收益的,有收益的按格式化之前的空间排序,有损耗的按照格式化之后的空间排序。前后一致的放中间。
代码:
#include<bits/stdc++.h>
#define int long long
#define Online_Judge
//#define dp
#define rint register int
using namespace std;
inline void read(int &a)
{
a=0;int b=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,ans=0x7fffffffffffffff,res=0,space=0,tim=0;
struct node{int st,en;}pan[2000006];
inline bool cmp(node A,node B)
{
if(A.st<A.en&&B.st<B.en)return A.st<B.st;
if(A.st>A.en&&B.st>B.en)return A.en>B.en;
if(A.st>A.en&&B.st<B.en)return false;
if(A.st<A.en&&B.st>B.en)return true;
if(A.st<A.en&&B.st==B.en)return true;
if(A.st>A.en&&B.st==B.en)return false;
if(A.st==A.en&&B.st<B.en)return false;
if(A.st==A.en&&B.st>B.en)return true;
return A.en+A.st<B.en+B.st;
}
signed main()
{
#ifdef dp
freopen("4.in","r",stdin);
freopen("3.out","w",stdout);
#endif
#ifdef Online_Judge
freopen("reformat.in","r",stdin);
freopen("reformat.out","w",stdout);
#endif
read(n);
for(rint i=1;i<=n;++i)
read(pan[i].st),read(pan[i].en);
res=0;space=0;
sort(pan+1,pan+n+1,cmp);
for(rint i=1;i<=n;++i)
{
if(pan[i].st>space)
{
res+=pan[i].st-space;
space=pan[i].en;
}
else
{
space-=pan[i].st;
space+=pan[i].en;
}
}
ans=min(ans,res);
printf("%lld\n",ans);
return 0;
}
「$idea$」$\mathcal{Chebyshev}$ $\mathcal{Distance}$ $\&$ $\mathcal{Manhattan}$ $\mathcal{Distance}$
切比雪夫距离与曼哈顿距离关系密切,因为它们可以相互转化。
切比雪夫转曼哈顿:$(x,y)->(\frac{x+y}2 , \frac{x-y}2)$
曼哈顿转切比雪夫:$(x,y)->(x+y,x-y)$
例题:$[TJOI2013]$松鼠聚会
题目大意:给出一个坐标系上的一些点为松鼠的家,定义点与点之间的距离为切比雪夫距离,求所有松鼠都到一个松鼠家里去所走的最小路径长度和。数据范围$n \leq 1e5 , |x|,|y| \leq 1e9$
题解:
先将原坐标系上的点$(x,y)$转化为$(x,y)->(\frac{x+y}2 , \frac{x-y}2)$,
原图上的切比雪夫距离随即转化为新图的曼哈顿距离。
答案就变成了$min{\sum\limits_{j=1}^n|x_i-x_j| + \sum\limits_{j=1}^n|y_i-y_j|}$
此时我们考虑分别对$x$和$y$排序,可以直接把绝对值去掉。
化简可得
$min\{(i-1)*x_i - \sum\limits_{j=1}^{i-1} x_j + \sum\limits_{j=i+1}^n x_j - (n-i)*x_i + i*y_i - \sum\limits_{j=1}^i y_j + \sum\limits_{j=i+1}^n y_j - (n-i)*y_i\}$
前缀和优化即可。
p.s.上面这个柿子我手打的,有什么错大家一定要指出来呀……
代码:
#include<bits/stdc++.h>
#define int long long
#define rint register int
using namespace std;
inline void read(int &a)
{
a=0;int b=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,ans=0x7fffffffffffffff;
int sxfrt[100005],sxbak[100005],syfrt[100005],sybak[100005],inx[100005],iny[100005];
int x[100005],y[100005];
signed main()
{
// freopen("1.in","r",stdin);
// freopen("1.out","w",stdout);
read(n);
for(rint i=1,stx,sty;i<=n;++i)
{
read(stx),read(sty);
x[i]=inx[i]=stx+sty;
y[i]=iny[i]=stx-sty;
}
sort(x+1,x+n+1);
sort(y+1,y+n+1);
for(rint i=1;i<=n;++i)
{
sxfrt[i]=sxfrt[i-1]+x[i],
syfrt[i]=syfrt[i-1]+y[i];
}
for(rint i=n;i>=1;--i)
{
sxbak[i]=sxbak[i+1]+x[i],
sybak[i]=sybak[i+1]+y[i];
}
for(rint i=1;i<=n;++i)
{
int res=0;
int res1=lower_bound(x+1,x+n+1,inx[i])-x;
int res2=lower_bound(y+1,y+n+1,iny[i])-y;
res+=(res1-1)*inx[i]-sxfrt[res1-1]+sxbak[res1+1]-(n-res1)*inx[i];
res+=(res2-1)*iny[i]-syfrt[res2-1]+sybak[res2+1]-(n-res2)*iny[i];
ans=min(ans,res);
}
printf("%lld\n",ans>>1);
return 0;
}
「非知识性失分」赛后收文件前「胡乱」更改文件
额,这个正式比赛应该不会存在问题。不过毕竟是校内比赛。。。
说一下痛苦的过程:
赛时的文件有人的没有收上来,老师就重新收了一遍。
然而收上去的是我赛后写的一个用来测试long double的代码。。。
为了图方便我直接在主目录的文件上更改的。于是60->0。
「题解」二叉搜索树:区间dp+剪枝
发现O(n^3)的暴力dp还是挺好想的。然而赛时我就是被模拟蒙蔽了双眼。
简要题解:
区间dp的一般形式:设$f_{i,j}$表示只考虑区间$i$到$j$的答案。
转移只需要在$i$到$j$之间枚举转移点$k$,使得$k$为区间$i$到$j$形成二叉搜索树的根节点。
转移方程:$f_{i,j}=f_{i,k-1}+f_{k+1,j}+\sum\limits_{l=i}^j x_i$。
优化:归纳证明可得上述转移存在决策单调性,所以我们记录一下每个区间的上一个转移点,枚举转移点的时候在$[i,j-1]$和$[i+1,j]$的转移点之间枚举即可。
中间出了一点小$bug$,就是说枚举$k$的时候会出现$k+1>n$的情况,不处理会$w70$,初始化一下不合法区间就可以了。
#include<bits/stdc++.h>
#define int long long
#define rint register int
using namespace std;
inline void read(int &a)
{
a=0;int b=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,x[5003],f[5003][5003],sum[5003],g[5003][5003];
signed main()
{
read(n);memset(f,0x3f,sizeof(f));
for(rint i=1;i<=n;++i)
{
read(x[i]),sum[i]=sum[i-1]+x[i];
f[i][i]=x[i],g[i][i]=i;
for(rint j=0;j<i;++j)f[i][j]=0;
}
for(rint i=0;i<=n+1;++i) f[n+1][i]=0;
for(rint i=2;i<=n;++i)for(rint j=1;j+i-1<=n;++j)
for(rint k=max(g[j][j+i-2],j);k<=max(g[j+1][j+i-1],j);++k)
if(f[j][k-1]+f[k+1][i+j-1]+(sum[i+j-1]-sum[j-1])<f[j][i+j-1])
f[j][i+j-1]=f[j][k-1]+f[k+1][i+j-1]+(sum[i+j-1]-sum[j-1]),g[j][i+j-1]=k;
printf("%lld\n",f[1][n]);
}
「题解」数列:exgcd
窝栽了。说真的我看出来$exgcd$了。也写出来了。但是不会用是硬伤。
$exgcd$主要用来解二元一次方程$ax+by=gcd(a,b)$的一组特解。根据这一组特解我们可以推广到$ax+by=c$中。根据裴蜀定理,当且仅当$gcd(a,b)|c$时,方程$ax+by=c$有解。
exgcd的简单证明:
对于方程$ax+by=gcd(a,b)$,令$a=b,b=a%b$,则有$b*x+a\%b*y=gcd(b,a\%b)$,
又$gcd(a,b)=gcd(b,a\%b)$,所以可得
$a*x+b*y=b*x+a\%b*b=b*x+(a-a/b*b)*y=a*y+b*(x-a/b*y)$
得证。
代码实现:
int exgcd(rint a,rint b,rint &x,rint &y)
{
if(!b)
{
x=1;y=0;
return a;
}
rint res=exgcd(b,a%b,x,y);
rint t=x;x=y;y=t-a/b*x;
return res;
}
简要题解:
关于数列这道题,我们需要运用$exgcd$先行解出一组特解。我们最终的目的是使得$abs(x)+abs(y)$最小,我们假设令$a<b$,那么答案一定在$x$取得正数最小值或负数最大值时取得。如果$a>b$,$swap$后再进行解决。
代码:
#include<bits/stdc++.h>
#define int long long
#define rint register int
using namespace std;
inline void read(rint &a)
{
a=0;rint b=1;register char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,A,B,a[100005],dist[200005],fx[4],ans;
bool vis[200005];
int exgcd(rint a,rint b,rint &x,rint &y)
{
if(!b){x=1;y=0;return a;}
rint res=exgcd(b,a%b,x,y);
rint t=x;x=y;y=t-a/b*x;
return res;
}
signed main()
{
// freopen("array.in","r",stdin);
// freopen("1.in","r",stdin);
// freopen("2.out","w",stdout);
read(n),read(A),read(B);
if(A>B)swap(A,B);rint x,y,gcd;
gcd=exgcd(A,B,x,y);
for(rint i=1;i<=n;++i)
{
read(a[i]);
if(a[i]%gcd){puts("-1");return 0;}
rint lx=x*a[i]/gcd,ly=y*a[i]/gcd;
// cout<<"lx:"<<lx<<" ly:"<<ly<<endl;
rint la=A/gcd,lb=B/gcd;
if(lx>0)
{
rint tag=lx/lb,res=0x7fffffffffffffff;
res=min(abs(lx-tag*lb)+abs(ly+tag*la),res);
res=min(abs(lx-(tag+1)*lb)+abs(ly+(tag+1)*la),res);
res=min(abs(lx-(tag-1)*lb)+abs(ly+(tag-1)*la),res);
ans+=res;
}
else
{
rint tag=(-lx)/lb,res=0x7fffffffffffffff;
res=min(abs(lx+tag*lb)+abs(ly-tag*la),res);
res=min(abs(lx+(tag+1)*lb)+abs(ly-(tag+1)*la),res);
res=min(abs(lx+(tag-1)*lb)+abs(ly-(tag-1)*la),res);
ans+=res;
}
}
printf("%lld\n",ans);
}
「题解」最小距离:多源最短路
说实话,从来没有接触过多源最短路。(或者是接触过我忘了??)
简要题解:
spfa最开始将所有源点都塞进队列,跑的时候记录一下每一个节点是被哪个源点更新的就完了。
代码:
#include<bits/stdc++.h>
#define int long long
#define rint register int
using namespace std;
const int N=200005,M=400005,inf=0x3f3f3f3f3f3f3f3f;
inline void read(rint &a)
{
a=0;rint b=1;register char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,m,p,v[M],w[M],nxt[M],first[N],tot;
int id[N],rk[N],ans[N],dist[N],gx[N],st[N],en[N],wi[N];
bool vis[N];
queue <int> q;
inline void build_line(int uu,int vv,int ww)
{
v[++tot]=vv,w[tot]=ww;
nxt[tot]=first[uu],first[uu]=tot;
}
inline void spfa()
{
for(rint i=1;i<=n;++i)
dist[i]=inf,vis[i]=0;
for(rint i=1;i<=p;++i)
gx[id[i]]=i,q.push(id[i]),dist[id[i]]=0;
while(!q.empty())
{
int x=q.front();q.pop();
for(rint i=first[x];i;i=nxt[i])
{
int y=v[i];
if(dist[x]+w[i]<dist[y])
{
dist[y]=w[i]+dist[x],gx[y]=gx[x];
if(!vis[y])vis[y]=1,q.push(y);
}
}
vis[x]=0;
}
return ;
}
signed main()
{
// freopen("distance.in","r",stdin);
read(n),read(m),read(p);
for(rint i=1;i<=p;++i)
read(id[i]),rk[id[i]]=i,ans[i]=inf;
for(rint i=1,ST,EN,WE;i<=m;++i)
{
read(ST),read(EN),read(WE);st[i]=ST,en[i]=EN,wi[i]=WE;
build_line(ST,EN,WE),build_line(EN,ST,WE);
}
spfa();
// for(rint i=1;i<=n;++i)
// cout<<dist[i]<<' '<<gx[i]<<endl;
// cout<<"----------------------"<<endl;
for(rint i=1;i<=m;++i)
{
if(gx[st[i]]!=gx[en[i]])
{
int res=dist[st[i]]+dist[en[i]]+wi[i];
// cout<<i<<' '<<st[i]<<' '<<en[i]<<' '<<res<<endl;
ans[gx[st[i]]]=min(ans[gx[st[i]]],res);
ans[gx[en[i]]]=min(ans[gx[en[i]]],res);
}
}
for(rint i=1;i<=p;++i)
printf("%lld ",ans[i]);puts("");
return 0;
}
/*
5 6 3
2 4 5
1 2 4
1 3 1
1 4 1
1 5 4
2 3 1
3 4 3
*/
「题解」数对:线段树优化dp
简要题解:
对于随机排部求最优解,考虑最优排部。
如果$a_i<b_j$并且$b_i<a_j$,则此时一定是$i$在$j$前更优。
(因为产生贡献当且仅当$a_i \leq b_j$,上述情况$i$在前可以产生贡献,$j$在前不能产生贡献。)
所以按照$a+b$排序后就是队长快跑的原题了。
之前有一个错解想法,具体是说按照$a_i$的大小建一棵树状数组,按$b_i$查询,按$a_i$修改。
然而后来证伪了。
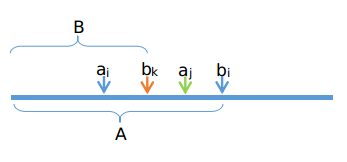
如上图,我们会用$A$区域的值去更新$i$,此时$a_j$的值被更新到了$a_i$身上。
然后会用$B$区域的值去更新$k$,此时会用$a_j$的值去更新$k$。
等于说我们间接使用$a_j$去更新了$b_k$,而这样的更新是不合法的!
所以在更新的过程中需要分两种情况。对于小于$a_i$的部分,直接取出最大值更新$a_i$单点即可。对于$a_i$和$b_i$之间的部分,我们需要用$i$的贡献去更新他们。线段树实现查询区间最大值、区间加、单点修改即可。
$debug$的时候出了点小问题,线段树下传的节点编号参数我一直喜欢写$k$,结构体内部维护的权值我也喜欢写$k$。本来嘛,因为命名空间不同不会出锅。我也觉得这没啥事。然而这次出锅了。我在$pushdown$中写了这样一句话:$t[k<<1|1],k+=lin$,中间的点写成了逗号。由于传进去的参也是$k$,所以编译没有报错。然后我就死了。所以以后还是要尽量改掉这个写法,传个$x$吧。
代码:
#include<bits/stdc++.h>
#define int long long
#define rint register int
using namespace std;
inline void read(rint &a)
{
a=0;rint b=1;register char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,lsh[200005],cnt,tot;
struct node{int k,lz;}t[1000006];
struct node2{int a,b,w;}p[100005];
inline bool cmp(node2 A,node2 B){return A.a+A.b<B.a+B.b;}
inline void pushdown(int k)
{
if(!t[k].lz)return ;
int lin=t[k].lz;t[k].lz=0;
t[k<<1].k+=lin,t[k<<1].lz+=lin;
t[k<<1|1].k+=lin,t[k<<1|1].lz+=lin;
return;
}
inline void update(int k){t[k].k=max(t[k<<1].k,t[k<<1|1].k);}
inline void add(int k,int l,int r,int L,int R,int dat)
{
if(L<=l&&r<=R)
{
t[k].k+=dat;
t[k].lz+=dat;
return ;
}
pushdown(k);int mid=(l+r)>>1;
if(L<=mid)add(k<<1,l,mid,L,R,dat);
if(R>mid)add(k<<1|1,mid+1,r,L,R,dat);
update(k);return ;
}
inline void change(int k,int l,int r,int p,int dat)
{
if(l==r)
{
t[k].k=max(t[k].k,dat);
return ;
}
pushdown(k);int mid=(l+r)>>1;
if(p<=mid)change(k<<1,l,mid,p,dat);
else change(k<<1|1,mid+1,r,p,dat);
update(k);return ;
}
inline int query(int k,int l,int r,int L,int R)
{
if(L>R)return 0;
if(L<=l&&r<=R)return t[k].k;
pushdown(k);int mid=(l+r)>>1,res=0;
if(L<=mid)res=max(query(k<<1,l,mid,L,R),res);
if(R>mid)res=max(query(k<<1|1,mid+1,r,L,R),res);
update(k);
return res;
}
signed main()
{
read(n);
for(rint i=1;i<=n;++i)
{
read(p[i].a),read(p[i].b),read(p[i].w);
lsh[++tot]=p[i].a,lsh[++tot]=p[i].b;
}
sort(lsh+1,lsh+tot+1);
cnt=unique(lsh+1,lsh+tot+1)-lsh-1;
for(rint i=1;i<=n;++i)
{
p[i].a=lower_bound(lsh+1,lsh+cnt+1,p[i].a)-lsh;
p[i].b=lower_bound(lsh+1,lsh+cnt+1,p[i].b)-lsh;
}
sort(p+1,p+n+1,cmp);
for(rint i=1;i<=n;++i)
{
if(p[i].b>p[i].a)
{
int res=query(1,1,cnt,1,p[i].a)+p[i].w;
change(1,1,cnt,p[i].a,res);
add(1,1,cnt,p[i].a+1,p[i].b,p[i].w);
}
else
{
int res=query(1,1,cnt,1,p[i].b)+p[i].w;
change(1,1,cnt,p[i].a,res);
}
}
printf("%lld\n",t[1].k);
return 0;
}
「题解」序列:三维偏序问题
这东西……我就算不能秒掉也不至于盯着发呆无所适从吧……我承认题目把我骗住了。还是实力不行没有看出来。
简要题解:
对$a$和$b$分别求前缀和,问题转化为了保证$a_{l-1} \leq a_r$并且$b_{l-1} \leq b_r$,求$r-l+1$的最大值。
考虑先进行离散化,然后按$suma$进行排序,然后就转化为了二维偏序问题。
顺序扫并将下标按$sumb$加入树状数组中,每次查询当前最小下标即可。
调代码的过程出现了一些小问题。答案减一其实没有必要。注意一下问题的转化:
$\sum\limits_{i=l}^r a_i \geq 0$并且$\sum\limits_{i=l}^r b_i \geq 0$求$r-l+1$的最大值
$ \Leftrightarrow $
$suma_{l-1} \leq suma_r$并且$sumb_{l-1} \leq sumb_r$求$r-l+1$的最大值。
所以我们查出来的下标其实是$l-1$,我们此时求的$id-query()$其实是$r-(l-1)=r-l+1$,已经没有必要额外加一了。
所以我加了个一反而画蛇添足。
代码:
#include<bits/stdc++.h>
#define int long long
#define rint register int
#define lowbit(A) A&-A
#define inf 0x7fffffffffffffff
using namespace std;
inline void read(rint &a)
{
a=0;rint b=1;register char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')b=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){a=(a<<3)+(a<<1)+ch-'0';ch=getchar();}
a=a*b;return ;
}
int n,a[500005],b[500005],ans,t[1000005],lsh[1000005],tot,cnt;
struct node{int a,b,id;}sum[500005];
inline bool cmp(node A,node B){return A.a<B.a;}
inline void add(int x,int dat){for(;x<=cnt;x+=lowbit(x))t[x]=min(t[x],dat);return ;}
inline int query(int x){int res=inf;for(;x;x-=lowbit(x))res=min(t[x],res);return res;}
signed main()
{
// freopen("sequence.in","r",stdin);
read(n);memset(t,0x7f,sizeof(t));
for(rint i=1;i<=n;++i)read(a[i]),sum[i].a=sum[i-1].a+a[i],lsh[++tot]=sum[i].a;
sum[0].a=sum[0].b=0,sum[0].id=0;lsh[++tot]=0;
for(rint i=1;i<=n;++i)read(b[i]),sum[i].b=sum[i-1].b+b[i],lsh[++tot]=sum[i].b,sum[i].id=i;
sort(lsh+1,lsh+tot+1);cnt=unique(lsh+1,lsh+tot+1)-lsh-1;
for(rint i=0;i<=n;++i)sum[i].a=lower_bound(lsh+1,lsh+cnt+1,sum[i].a)-lsh;
for(rint i=0;i<=n;++i)sum[i].b=lower_bound(lsh+1,lsh+cnt+1,sum[i].b)-lsh;
sort(sum,sum+n+1,cmp);
for(rint i=0;i<=n;++i)ans=max(ans,sum[i].id-query(sum[i].b)+1),add(sum[i].b,sum[i].id);
printf("%lld\n",ans-1);
return 0;
}
 $\mathcal{The}$ $\mathcal{end}$
$\mathcal{The}$ $\mathcal{end}$

