Algorithm

算法分析与代码实现

LCSS

最长公共子序列（Longest-Common-Subsequence） 

核心代码

            for (int i = 0; i < ArrayLengthA; ++i) {
                for (int j = 0; j < ArrayLengthB; ++j) {
                       if (SequenceA[i].equals(SequenceB[j])) {
                           Lcs[i + 1][j + 1] = Lcs[i][j] + 1;
                           Flag[i + 1][j + 1] = 1;                //1:ok 2:left 3:up
                       }else if (Lcs[i + 1][j] > Lcs[i][j + 1]) {
                           Lcs[i + 1][j + 1] = Lcs[i + 1][j];
                           Flag[i + 1][j + 1] = 2;
                       }else {
                           Lcs[i + 1][j + 1] = Lcs[i][j + 1];
                           Flag[i + 1][j + 1] = 3;
                       }
                   }
            }

 

序列的回溯

        public void getLongestCommonSubsequence(int[][] Flag, String[] SequenceA, int LengthA, int LengthB) {
            if (Flag[LengthA][LengthB] == 1) {
                getLongestCommonSubsequence(Flag, SequenceA, LengthA - 1, LengthB - 1);
                this.LongestCommonSubsequence.add(SequenceA[LengthA - 1]);
            }else if (Flag[LengthA][LengthB] == 2) {
                getLongestCommonSubsequence(Flag, SequenceA, LengthA, LengthB - 1);
            }else if (Flag[LengthA][LengthB] == 3) {
                getLongestCommonSubsequence(Flag, SequenceA, LengthA - 1, LengthB);
            }
        }

 

算法过程分析

 

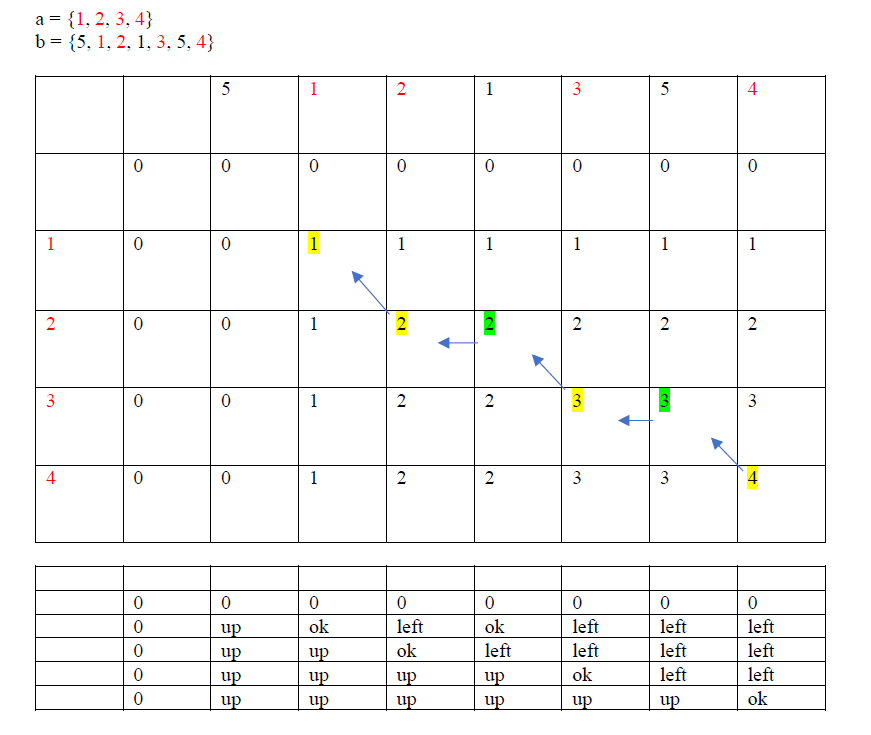
DTW

动态时间规划（Dynamic Time Warping）求解两序列最小距离

核心代码

            for (int i = 0; i < LengthA; ++i) {
                for (int j = 0; j < LengthB; ++j) {
                    if (i == 0 && j == 0) {
                        this.SumDistance[i][j] = this.Distance[0][0];
                        DistanceTmp1 = 0.0;
                        DistanceTmp2 = 0.0;
                        DistanceTmp3 = 0.0;
                    }
                    if (i == 0 && j > 0) {
                        DistanceTmp1 = 1000000.0;
                        DistanceTmp2 = this.SumDistance[i][j - 1];
                        DistanceTmp3 = 1000000.0;
                    }
                    if (i > 0 && j == 0) {
                        DistanceTmp1 = this.SumDistance[i - 1][j];
                        DistanceTmp2 = 1000000.0;
                        DistanceTmp3 = 1000000.0;
                    }
                    if (i > 0 && j > 0) {
                        DistanceTmp1 = this.SumDistance[i - 1][j];
                        DistanceTmp2 = this.SumDistance[i][j - 1];
                        DistanceTmp3 = this.SumDistance[i - 1][j - 1];
                    }
                    this.SumDistance[i][j] = this.Distance[i][j] + Math.min(DistanceTmp1, Math.min(DistanceTmp2, DistanceTmp3));
                }
            }

算法原理 

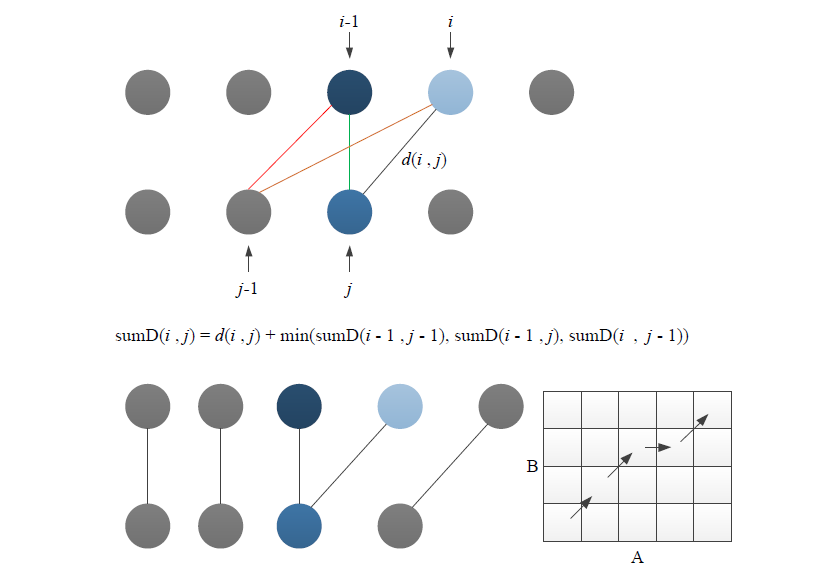
算法过程分析

 

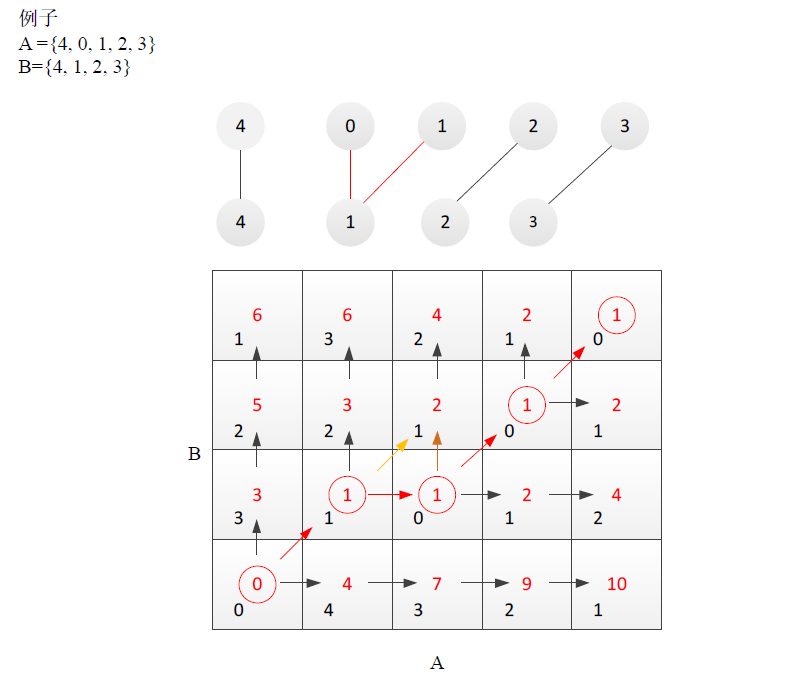
长串中寻找最长重复子串

不断将子串的串长增长，并向后移动起始位置进行匹配

核心代码

            for (int i = 1; i < OriginalString.length; ++i) {
                for (int j = 0; j < OriginalString.length - i; ++j) {
                    if (OriginalString[j].equals(OriginalString[i + j])) {
                        TempLength++;
                    } else {
                        TempLength = 0;
                    }
                    if (TempLength > MaxLength) {
                        MaxLength = TempLength;
                        First = j - TempLength + 1;
                    }
                    if ((i + j + 1) == OriginalString.length) {
                        TempLength = 0;
                    }
                }
            }

 

 算法过程分析

 

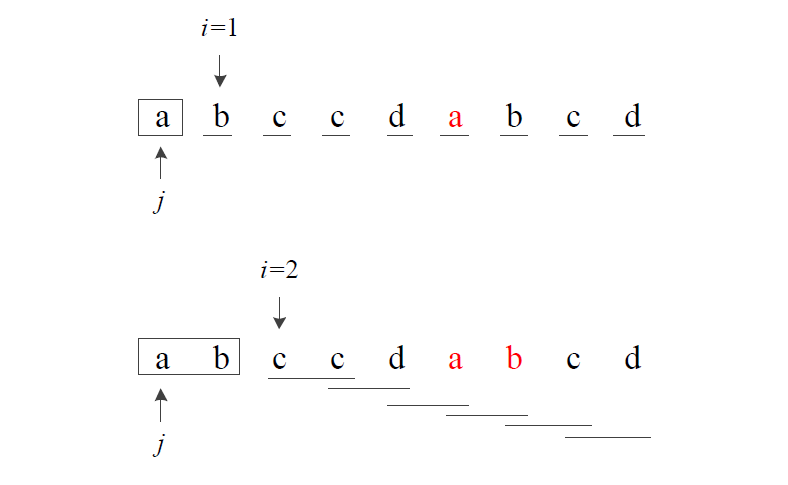
KMP

匹配模式主串，时间复杂度O(m+n)

核心代码

        //next数组的构建        
        public void getNext(String[] StringP) {
            this.Next = new int[StringP.length];
            this.Next[0] = -1;
            int PointerJ = 0;
            int PointerK = -1;
            while (PointerJ < StringP.length - 1) {
               if (PointerK == -1 || StringP[PointerJ] == StringP[PointerK]) {
                   if (StringP[++PointerJ] == StringP[++PointerK]) { // 当两个字符相等时要跳过
                       this.Next[PointerJ] = this.Next[PointerK];
                   } else {
                       this.Next[PointerJ] = PointerK;
                   }
               } else {
                   PointerK = this.Next[PointerK];
               }
            }
        }

 

 

            //模式匹配
            while (PointerI < StringT.length && PointerJ < StringP.length) {
               if (PointerJ == -1 || StringT[PointerI] == StringP[PointerJ]) { // 当j为-1时，要移动的是i，当然j也要归0
                   PointerI++;
                   PointerJ++;
               } else {
                   PointerJ = this.Next[PointerJ];
               }
            }
            if (PointerJ == StringP.length) {
               return PointerI - PointerJ;
            } else {
               return -1;
            }

 

算法原理以及过程分析

 

---

 

 完整代码：https://github.com/xinglicha0/algorithm