梯度下降和反向传播

由于本人知识有限，如有写错的地方，还请谅解并指出，谢谢！

1、梯度下降

预备知识

目标函数：f(x) = w*x+b ，在给定的训练集中有(X,Y)，X为输入参数，Y为输出结果。我们需要找到一组w和b，使的w*x+b 的值接近Y，并且误差最小，那么f(x) = w*x+b 就是目标函数。根据已知的参数w和b，可以求的目标函数的值为多少。

 

损失函数：训练得到的结果与实际结果的误差。在训练中，我们是需要不断的调整参数w和b的值，使的结果更好，误差尽可能的小。一开始我们有初始值参数w和b，然后根据损失情况不断调整参数w和b。在已知输入参数x情况下，我们可得f(x) = w*x+b ,我们要使的损失函数L(Y, f(X)) = (Y - f(X))²尽可能的小就行，当然也不能太小了，不然会过拟合，也不能太大了，否则就会欠拟合。也有一些其他的损失函数，这里提到的是平方损失（Square Loss）。

1.1 损失函数可视化

在线性回归中，参数w常常是高维的，那么直接可视化就不太可能，我们需要将它投射到一维或二维上，才方便可视化。以一维线性回归为例，y = w₁x₁+b₁。损失函数可能为如下图所示：

 

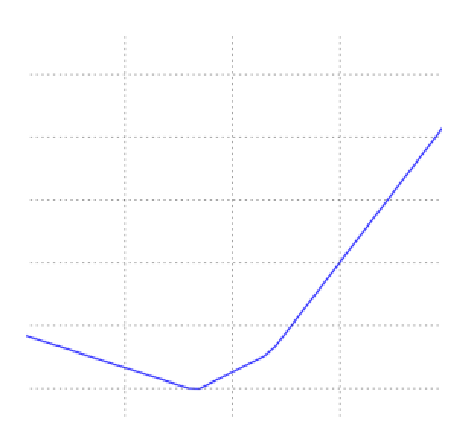
如果有两个维度，损失函数可能入下两图所示：

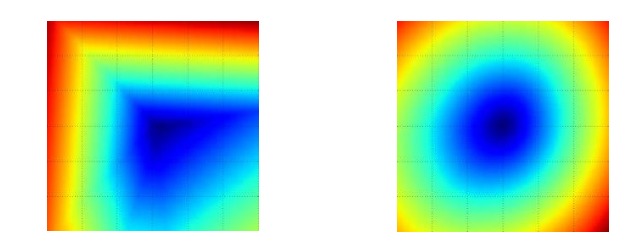
蓝色越深表示损失函数越低，红色越深表示损失函数越高。

1.2 最优化

损失函数是凸函数时，能得到全局最低点。如果是一个非凸函数，那么进行梯度下降时得到的可能是局部最小值，而不是全局最小值。但不是凸函数时就需要一些优化使的得到的尽量是全局最小值，跳出局部最小值。

下图左边的蓝色为局部最小值，右边的蓝色为全局最小值。

 

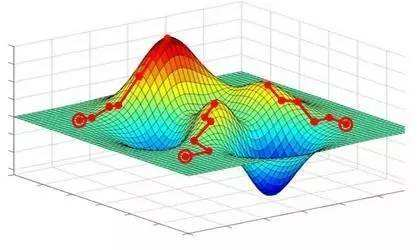
对于SVM来说，SVM的损失函数就是一个凸函数，凸函数的正系数加和也是一个凸函数，但扩充到神经网络之后，损失函数就变成了一个非凸函数了，这就需要优化了。

 1.2.1 随机搜寻

最直接的方法是尽可能多的去尝试参数，是的损失函数尽可能的小，但不太实用，太随机性了。

1.2.2 随机局部搜索

在现有参数W的基础上，搜寻下附近的点，每次更新损失函数最小的值。如果得到了局部最小值，也有可能在附近搜寻的时候跳出局部最小值，这样得到全局最小值的几率大大增加。

1.2.3 顺这梯度下降

找到最陡的方向，迈一小步，然后再找最陡的方向，再迈一小步..... 就向下山一样，每次从最陡的方向下山，能更快的达到山低，只是这样有可能被困在局部最小值。

1.3 梯度下降

 计算梯度有两种方法：

① 数值梯度：慢一些但简单；

②解析梯度：速度快但更容易出错。

数值梯度对于每个维度，都在原始值上加上一个很小的h，然后计算这个维度的偏导。公式：。

解析梯度是根据公式来计算它的偏导。

 

我们可以先计算解析梯度和数值梯度，然后对比结果和纠正，就可以大胆的使用解析梯度了，这个过程叫做：梯度检查/检测

 

梯度下降：就是在不断的迭代，每次按梯度的反方向更新参数，直到最终的参数能使的误差最小就行了。就如下图所示，每次按梯度下降的方向走，最终能得到比较小的值。

 

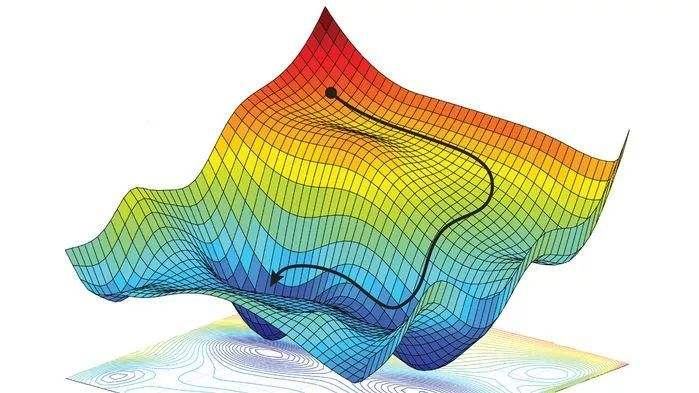
2、反向传播

2.1 链式法则

若函数u =φ(x)，v =ψ(x)在x点可导，z = f(u, v) 有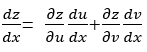

比如函数f(x,y,z) = x*(y+z) 令u = (y+z) ,那么df/dz = df/du * du/dz 这就是链式法则。

 

2.2 Sigmod例子

Sigmod函数 σ(z) =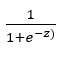 ，z = wx。

以sigmod函数为例：

 

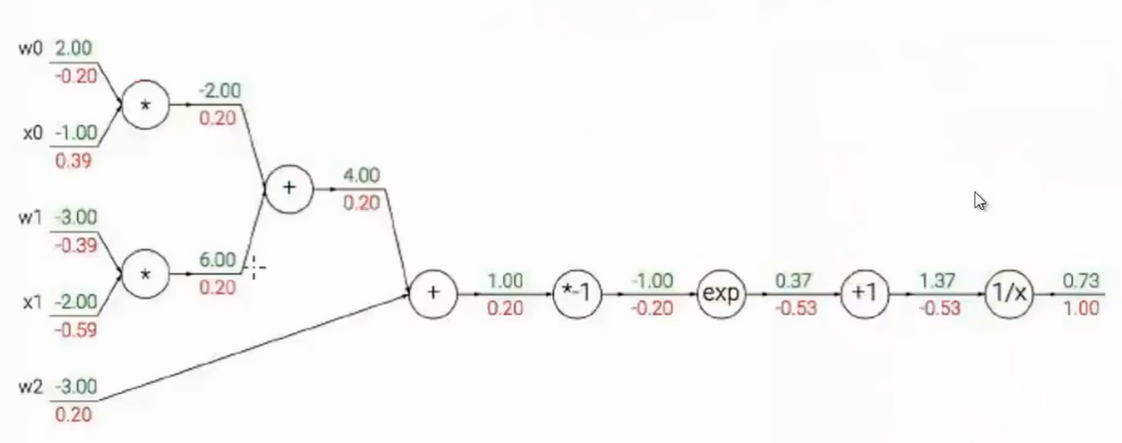
Sigmod函数有如下性质。dσ(z)/dz = (1-σ(z))(z)。由于偏导可以用本身表达，那么将sigmod用在反向传播上的计算将减少好多。

以下面的神经网络来计算反向传播：

 

 

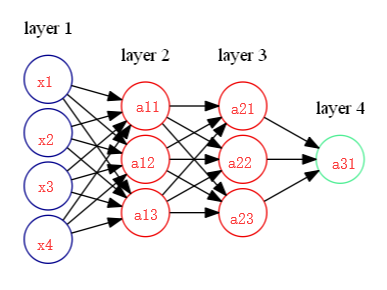
a₁₁ = σ(w₁₁*x₁+w₁₂*x₂+w₁₃*x₃+w₁₄*x₄) ... a₃₁ = σ(w₃₁*a₂₁+w₃₂*a₂₂+w₃₃*a₂₃)

 

假设我们要计算da₃₁/ dx₁，那么da₃₁/ dx₁ =  da₃₁/ dz₃₁ * dz₃₁/da₂₁ * da₂₁/dz₂₁ * dz₂₁/da₁₁ * da₁₁/dz₁₁ * dz₁₁/dx₁, 

因为z_i = w_ix_i-1 或 w_ia_i-1， 那么dz_i/da_i-1 = w_i。由于ai = σ(zi), dσ(z)/dz = (1-σ(z))(z) 那么 da_i/dz_i = (1-σ(z_i))(z_i) , 这样我们就可以得到da31/dx1的值了。

其他参数也一样，这样反向传播的值就可以根据正向传播的值快速得到，然后按梯度下降的方向更新参数，直到找到一个最小值为止。