Codeforces Round #495 (Div. 2) ABCD

A. Sonya and Hotels

Sonya decided that having her own hotel business is the best way of earning money because she can profit and rest wherever she wants.

The country where Sonya lives is an endless line. There is a city in each integer coordinate on this line. She has $\mathrm{nn hotels,\; where\; the ii-th\; hotel\; is\; located\; in\; the\; city\; with\; coordinate xixi.\; Sonya\; is\; a\; smart\; girl,\; so\; she\; does\; not\; open\; two\; or\; more\; hotels\; in\; the\; same\; city.}$

Sonya understands that her business needs to be expanded by opening new hotels, so she decides to build one more. She wants to make the minimum distance from this hotel to all others to be equal to $\mathrm{dd.\; The\; girl\; understands\; that\; there\; are\; many\; possible\; locations\; to\; construct\; such\; a\; hotel.\; Thus\; she\; wants\; to\; know\; the\; number\; of\; possible\; coordinates\; of\; the\; cities\; where\; she\; can\; build\; a\; new\; hotel.}$

Because Sonya is lounging in a jacuzzi in one of her hotels, she is asking you to find the number of cities where she can build a new hotel so that the minimum distance from the original $\mathrm{nn hotels\; to\; the\; new\; one\; is\; equal\; to dd.}$

Input

The first line contains two integers $\mathrm{nn and dd (1\le n\le 1001\le n\le 100, 1\le d\le 1091\le d\le 109) —\; the\; number\; of\; Sonya\text{'}s\; hotels\; and\; the\; needed\; minimum\; distance\; from\; a\; new\; hotel\; to\; all\; others.}$

The second line contains $\mathrm{nn different\; integers\; in\; strictly\; increasing\; order x1,x2,\dots ,xnx1,x2,\dots ,xn (-109\le xi\le 109-109\le xi\le 109) —\; coordinates\; of\; Sonya\text{'}s\; hotels.}$

Output

Print the number of cities where Sonya can build a new hotel so that the minimum distance from this hotel to all others is equal to $\mathrm{dd.}$

Examples

input

Copy

4 3
-3 2 9 16

output

Copy

6

input

Copy

5 2
4 8 11 18 19

output

Copy

5

Note

In the first example, there are $\mathrm{66 possible\; cities\; where\; Sonya\; can\; build\; a\; hotel.\; These\; cities\; have\; coordinates -6-6, 55, 66, 1212, 1313,\; and 1919.}$

In the second example, there are $\mathrm{55 possible\; cities\; where\; Sonya\; can\; build\; a\; hotel.\; These\; cities\; have\; coordinates 22, 66, 1313, 1616,\; and 2121.}$

$\mathrm{求有多少个点与已知的点最小的距离是3}$

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int a[N], n, x, d;
int main() {
    cin >> n >> d;
    for(int i = 0; i < n; i ++) cin >> a[i];
    sort(a,a+n);
    int ans = 2;
    for(int i = 0; i < n-1; i ++) {
        if(a[i+1]-a[i]-2*d > 0) ans += 2;
        else if(a[i+1]-a[i]-2*d == 0) ans++;
    }
    cout << ans << endl;
    return 0;
}

B. Sonya and Exhibition

Sonya decided to organize an exhibition of flowers. Since the girl likes only roses and lilies, she decided that only these two kinds of flowers should be in this exhibition.

There are $\mathrm{nn flowers\; in\; a\; row\; in\; the\; exhibition.\; Sonya\; can\; put\; either\; a\; rose\; or\; a\; lily\; in\; the ii-th\; position.\; Thus\; each\; of nn positions\; should\; contain\; exactly\; one\; flower:\; a\; rose\; or\; a\; lily.}$

She knows that exactly $\mathrm{mm people\; will\; visit\; this\; exhibition.\; The ii-th\; visitor\; will\; visit\; all\; flowers\; from lili to riri inclusive.\; The\; girl\; knows\; that\; each\; segment\; has\; its\; own beauty that\; is\; equal\; to\; the\; product\; of\; the\; number\; of\; roses\; and\; the\; number\; of\; lilies.}$

Sonya wants her exhibition to be liked by a lot of people. That is why she wants to put the flowers in such way that the sum of beauties of all segments would be maximum possible.

Input

The first line contains two integers $\mathrm{nn and mm (1\le n,m\le 1031\le n,m\le 103) —\; the\; number\; of\; flowers\; and\; visitors\; respectively.}$

Each of the next $\mathrm{mm lines\; contains\; two\; integers lili and riri (1\le li\le ri\le n1\le li\le ri\le n),\; meaning\; that ii-th\; visitor\; will\; visit\; all\; flowers\; from lili to ririinclusive.}$

Output

Print the string of $\mathrm{nn characters.\; The ii-th\; symbol\; should\; be\; «0»\; if\; you\; want\; to\; put\; a\; rose\; in\; the ii-th\; position,\; otherwise\; «1»\; if\; you\; want\; to\; put\; a\; lily.}$

If there are multiple answers, print any.

Examples

input

Copy

5 3
1 3
2 4
2 5

output

Copy

01100

input

Copy

6 3
5 6
1 4
4 6

output

Copy

110010

Note

In the first example, Sonya can put roses in the first, fourth, and fifth positions, and lilies in the second and third positions;

• in the segment $[1\dots 3][1\dots 3],\; there\; are\; one\; rose\; and\; two\; lilies,\; so\; the beauty is\; equal\; to 1\cdot 2=21\cdot 2=2;$
• in the segment $[2\dots 4][2\dots 4],\; there\; are\; one\; rose\; and\; two\; lilies,\; so\; the beauty is\; equal\; to 1\cdot 2=21\cdot 2=2;$
• in the segment $[2\dots 5][2\dots 5],\; there\; are\; two\; roses\; and\; two\; lilies,\; so\; the beauty is\; equal\; to 2\cdot 2=42\cdot 2=4.$

The total beauty is equal to $\mathrm{2+2+4=82+2+4=8.}$

In the second example, Sonya can put roses in the third, fourth, and sixth positions, and lilies in the first, second, and fifth positions;

• in the segment $[5\dots 6][5\dots 6],\; there\; are\; one\; rose\; and\; one\; lily,\; so\; the beauty is\; equal\; to 1\cdot 1=11\cdot 1=1;$
• in the segment $[1\dots 4][1\dots 4],\; there\; are\; two\; roses\; and\; two\; lilies,\; so\; the beauty is\; equal\; to 2\cdot 2=42\cdot 2=4;$
• in the segment $[4\dots 6][4\dots 6],\; there\; are\; two\; roses\; and\; one\; lily,\; so\; the beauty is\; equal\; to 2\cdot 1=22\cdot 1=2.$

The total beauty is equal to $\mathrm{1+4+2=71+4+2=7.}$

有m个区间，每个区间的0的个数乘以1的个数，求总和最大时，这个区间是怎么排列的。

全是010101...这样的排列就行。

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n, m, l, r;
    cin >> n >> m;
    for(int i = 1; i <= m; i ++) {
        cin >> l >> r;
    }
    for(int i = 0; i < n; i ++) {
        if(i&1)printf("0");
        else printf("1");
    }
    printf("\n");
    return 0;
}

C. Sonya and Robots

Since Sonya is interested in robotics too, she decided to construct robots that will read and recognize numbers.

Sonya has drawn $\mathrm{nn numbers\; in\; a\; row, aiai is\; located\; in\; the ii-th\; position.\; She\; also\; has\; put\; a\; robot\; at\; each\; end\; of\; the\; row\; (to\; the\; left\; of\; the\; first\; number\; and\; to\; the\; right\; of\; the\; last\; number).\; Sonya\; will\; give\; a\; number\; to\; each\; robot\; (they\; can\; be\; either\; same\; or\; different)\; and\; run\; them.\; When\; a\; robot\; is\; running,\; it\; is\; moving\; toward\; to\; another\; robot,\; reading\; numbers\; in\; the\; row.\; When\; a\; robot\; is\; reading\; a\; number\; that\; is\; equal\; to\; the\; number\; that\; was\; given\; to\; that\; robot,\; it\; will\; turn\; off\; and\; stay\; in\; the\; same\; position.}$

Sonya does not want robots to break, so she will give such numbers that robots will stop before they meet. That is, the girl wants them to stop at different positions so that the first robot is to the left of the second one.

For example, if the numbers $[1,5,4,1,3][1,5,4,1,3] are\; written,\; and\; Sonya\; gives\; the\; number 11 to\; the\; first\; robot\; and\; the\; number 44 to\; the\; second\; one,\; the\; first\; robot\; will\; stop\; in\; the 11-st\; position\; while\; the\; second\; one\; in\; the 33-rd\; position.\; In\; that\; case,\; robots\; will\; not\; meet\; each\; other.\; As\; a\; result,\; robots\; will\; not\; be\; broken.\; But\; if\; Sonya\; gives\; the\; number 44 to\; the\; first\; robot\; and\; the\; number 55 to\; the\; second\; one,\; they\; will\; meet\; since\; the\; first\; robot\; will\; stop\; in\; the 33-rd\; position\; while\; the\; second\; one\; is\; in\; the 22-nd\; position.$

Sonya understands that it does not make sense to give a number that is not written in the row because a robot will not find this number and will meet the other robot.

Sonya is now interested in finding the number of different pairs that she can give to robots so that they will not meet. In other words, she wants to know the number of pairs ($\mathrm{pp, qq),\; where\; she\; will\; give pp to\; the\; first\; robot\; and qq to\; the\; second\; one.\; Pairs\; (pipi, qiqi)\; and\; (pjpj, qjqj)\; are\; different\; if pi\ne pjpi\ne pj or qi\ne qjqi\ne qj.}$

Unfortunately, Sonya is busy fixing robots that broke after a failed launch. That is why she is asking you to find the number of pairs that she can give to robots so that they will not meet.

Input

The first line contains a single integer $\mathrm{nn (1\le n\le 1051\le n\le 105) —\; the\; number\; of\; numbers\; in\; a\; row.}$

The second line contains $\mathrm{nn integers a1,a2,\dots ,ana1,a2,\dots ,an (1\le ai\le 1051\le ai\le 105) —\; the\; numbers\; in\; a\; row.}$

Output

Print one number — the number of possible pairs that Sonya can give to robots so that they will not meet.

Examples

input

Copy

5
1 5 4 1 3

output

Copy

9

input

Copy

7
1 2 1 1 1 3 2

output

Copy

7

Note

In the first example, Sonya can give pairs ($\mathrm{11, 11),\; (11, 33),\; (11, 44),\; (11, 55),\; (44, 11),\; (44, 33),\; (55, 11),\; (55, 33),\; and\; (55, 44).}$

In the second example, Sonya can give pairs ($\mathrm{11, 11),\; (11, 22),\; (11, 33),\; (22, 11),\; (22, 22),\; (22, 33),\; and\; (33, 22).}$

求有多少个p,q  使的从左边遇见第一个p，从右边遇见第一个q没有交叉。

从左到右遍历一遍，当前这个数没有使用时就计算下右边有多少个不重复的数就行。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+10;
int a[N], n;
map<int,int> mp;
bool vis[N];
int main() {
    cin >> n;
    int cnt = 0;
    for(int i = 0; i < n; i ++) {
        cin >> a[i];
        if(!mp.count(a[i])) {
            cnt ++;
        }
        mp[a[i]] ++;
    }
    ll ans = 0;
    for(int i = 0; i < n; i ++) {
        mp[a[i]]--;
        if(mp[a[i]] == 0) cnt--;
        if(!vis[a[i]]) {
            ans += 1LL*cnt;
            vis[a[i]] = 1;
        }
    }
    cout << ans << endl;
    return 0;
}

D. Sonya and Matrix

Since Sonya has just learned the basics of matrices, she decided to play with them a little bit.

Sonya imagined a new type of matrices that she called rhombic matrices. These matrices have exactly one zero, while all other cells have the Manhattan distance to the cell containing the zero. The cells with equal numbers have the form of a rhombus, that is why Sonya called this type so.

The Manhattan distance between two cells (${\mathrm{x1x1, y1y1)\; and\; (x2x2, y2y2)\; is\; defined\; as |x1-x2|+|y1-y2||x1-x2|+|y1-y2|.\; For\; example,\; the\; Manhattan\; distance\; between\; the\; cells (5,2)(5,2) and (7,1)(7,1) equals\; to |5-7|+|2-1|=3|5-7|+|2-1|=3.}}^{}$

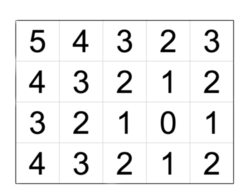Example of a rhombic matrix.

Note that rhombic matrices are uniquely defined by $\mathrm{nn, mm,\; and\; the\; coordinates\; of\; the\; cell\; containing\; the\; zero.}$

She drew a $\mathrm{n\times mn\times m rhombic\; matrix.\; She\; believes\; that\; you\; can\; not\; recreate\; the\; matrix\; if\; she\; gives\; you\; only\; the\; elements\; of\; this\; matrix\; in\; some\; arbitrary\; order\; (i.e.,\; the\; sequence\; of n\cdot mn\cdot m numbers).\; Note\; that\; Sonya\; will\; not\; give\; you nn and mm,\; so\; only\; the\; sequence\; of\; numbers\; in\; this\; matrix\; will\; be\; at\; your\; disposal.}$

Write a program that finds such an $\mathrm{n\times mn\times m rhombic\; matrix whose\; elements\; are\; the\; same\; as\; the\; elements\; in\; the\; sequence\; in\; some\; order.}$

Input

The first line contains a single integer $\mathrm{tt (1\le t\le 1061\le t\le 106) —\; the\; number\; of\; cells\; in\; the\; matrix.}$

The second line contains $\mathrm{tt integers a1,a2,\dots ,ata1,a2,\dots ,at (0\le ai<t0\le ai<t) —\; the\; values\; in\; the\; cells\; in\; arbitrary\; order.}$

Output

In the first line, print two positive integers $\mathrm{nn and mm (n\times m=tn\times m=t) —\; the\; size\; of\; the\; matrix.}$

In the second line, print two integers $\mathrm{xx and yy (1\le x\le n1\le x\le n, 1\le y\le m1\le y\le m) —\; the\; row\; number\; and\; the\; column\; number\; where\; the\; cell\; with 00 is\; located.}$

If there are multiple possible answers, print any of them. If there is no solution, print the single integer $-1-1.$

Examples

input

Copy

20
1 0 2 3 5 3 2 1 3 2 3 1 4 2 1 4 2 3 2 4

output

Copy

4 5
2 2

input

Copy

18
2 2 3 2 4 3 3 3 0 2 4 2 1 3 2 1 1 1

output

Copy

3 6
2 3

input

Copy

6
2 1 0 2 1 2

output

Copy

-1

Note

You can see the solution to the first example in the legend. You also can choose the cell $(2,2)(2,2) for\; the\; cell\; where 00 is\; located.\; You\; also\; can\; choose\; a 5\times 45\times 4 matrix\; with\; zero\; at (4,2)(4,2).$

In the second example, there is a $\mathrm{3\times 63\times 6 matrix,\; where\; the\; zero\; is\; located\; at (2,3)(2,3) there.}$

In the third example, a solution does not exist.

给定n个数，求是否存在n*m的矩阵，使的给定的条件成立，并求出0的坐标。一个矩阵，旋转180还是类似的。

所以假设0的坐标为(x , y)，到(1, 1)的距离是a, 到(n , m)的距离是b，其中b是给定的最大的数字。并且有：

x-1+y-1 = a    　　n-x+m-y = b

所以有n+m = a + b + 2

并且可以得到y = n+m-b-x

b和x是已知的，然后遍历所以存在的n,m就行。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int a[N], n, x, c[N], t;
int main() {
    cin >> t;
    int b = 0, m, xx, y;
    for(int i = 0; i < t; i ++) {
        scanf("%d", &x);
        a[x]++;
        b = max(b, x);
    }
    xx = 1;
    for(int i = 1; a[i] ; i ++) {
        if(a[i] != 4*i) {
            xx = i;
            break;
        }
    }
    for(int n = 1; n <= t; n ++) {
        if(t%n == 0) {
            memset(c, 0, sizeof(c));
            m = t/n;
            y = n+m-b-xx;
            for(int i = 1; i <= n; i ++) {
                for(int j = 1; j <= m; j ++) {
                    c[abs(i-xx)+abs(j-y)]++;
                }
            }
            bool flag = 1;
            for(int i = 0; i <= b; i ++) {
                if(a[i] != c[i]) {
                    flag = 0;
                    break;
                }
            }
            if(flag) {
                return 0*printf("%d %d\n%d %d\n",n,m,xx,y);
            }
        }
    }
    printf("-1\n");
    return 0;
}