ACM-ICPC Asia Training League 暑假第一阶段第三场 BFGHIK
B Bounty Hunter II
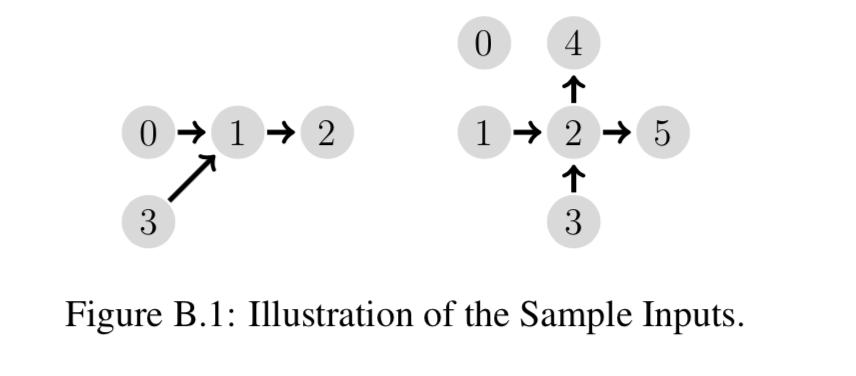
Spike the bounty hunter is tracking another criminal through space. Luckily for him hyperspace travel has made the task of visiting several planets a lot easier. Each planet has a number of Astral Gates; each gate connects with a gate on another planet. These hyperspace connections are, for obvious safety reasons, one-way only with one gate being the entry point and the other gate being the exit point from hyperspace. Furthermore, the network of hyperspace connections must be loop-free to prevent the Astral Gates from exploding, a tragic lesson learned in the gate accident of 20222022 that destroyed most of the moon.
While looking at his star map Spike wonders how many friends he needs to conduct a search on every planet. Each planet should not be visited by more than one friend otherwise the criminal might get suspicious and flee before he can be captured. While each person can start at a planet of their choosing and travel along the hyperspace connections from planet to planet they are still bound by the limitations of hyperspace travel.
Input Format
The input begins with an integer NN specifying the number of planets (0 < N \le 1000)(0<N≤1000). The planets are numbered from 00 to N-1N−1. The following NN lines specify the hyperspace connections.
The i-th of those lines first contains the count of connections KK (0\le K\le N-1)(0≤K≤N−1) from planet ii followed by KK integers specifying the destination planets.
Output Format
Output the minimum number of persons needed to visit every planet.
样例输入1
4 1 1 1 2 0 1 1
样例输出1
2
样例输入2
6 0 1 2 2 4 5 1 2 0 0
样例输出2
4
在一个有向图中,求最少可以分人一条路径,是的每个路径的顶点都不重复。可以转换成求二分图最大匹配
1 #include <bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 #define ll long long 4 using namespace std; 5 const int N = 2e3+10; 6 int edge[N][N], vis[N], match[N]; 7 int n, k, v, u; 8 9 bool dfs(int v) { 10 for(int i = n; i < 2*n; i ++) { 11 if(edge[v][i] && !vis[i]) { 12 vis[i] = 1; 13 if(match[i] == -1 || dfs(match[i])) { 14 match[i] = v; 15 return true; 16 } 17 } 18 } 19 return false; 20 } 21 int max_match() { 22 int res = 0; 23 memset(match, -1, sizeof(match)); 24 for(int i = 0; i < n; i ++) { 25 if(match[i] < 0) { 26 memset(vis, 0, sizeof(vis)); 27 if(dfs(i)) res++; 28 } 29 } 30 return res; 31 } 32 int main() { 33 cin >> n; 34 for(int i = 0; i < n; i ++) { 35 cin >> k; 36 for(int j = 0; j < k; j ++) { 37 cin >> v; 38 edge[i][v+n] = 1; 39 } 40 } 41 cout << n-max_match() << endl; 42 return 0; 43 }
F Divisions
David is a young boy and he loves numbers. Recently he learned how to divide two numbers.David divides the whole day. He is happy if the result of the division is an integer, but he is not very amused if this is not the case. After quite a while he decided to use only a single dividend each day.
The parents of David are very careful and they would like to ensure that David experiences enough happiness. Therefore they decide which number David will use as the dividend for this day.
There is still a problem: The parents are not very good at math and don’t know how to calculate the number of positive integral divisors for a given dividend N , which lead to an integral result.Now it’s up to you to help David’s parents.
Input
The single input line contains the single integer N , where N is chosen as a dividend (1 ≤ N ≤10^{18}1018).
Output
Print the number of positive integral divisors of N that lead to an integral result of the division.
样例输入1
12
样例输出1
6
样例输入2
999999999999999989
样例输出2
2
求一个数的因子有多少个,主要是求素因子,知道素因子了就很好求了。用的是随机算法,网上找的模板
1 #include <bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 #define ll long long 4 using namespace std; 5 const int N = 1e5+10; 6 ll a[N], tot; 7 8 ll mod_mul(ll a, ll b, ll n){ 9 ll cnt = 0LL; 10 while(b){ 11 if(b&1LL) cnt = (cnt+a)%n; 12 a=(a+a)%n; 13 b >>= 1LL; 14 } 15 return cnt; 16 } 17 ll mod_exp(ll a, ll b, ll n){ 18 ll res = 1LL; 19 while(b){ 20 if(b&1LL) res = mod_mul(res,a,n); 21 a = mod_mul(a,a,n); 22 b >>= 1LL; 23 } 24 return res; 25 } 26 bool ispirme(ll n){ 27 int respat = 5; 28 if(n==2LL || n==3LL || n==5LL || n==7LL || n==11LL) return true; 29 if(n==1 || !(n%2) || !(n%3) || !(n%5) || !(n%7) || !(n%11)) return false; 30 31 int k = 0; 32 ll d = n-1; 33 34 while(!(d&1LL)){ 35 k++; d >>= 1LL; 36 } 37 srand((ll)time(0)); 38 for(int i = 0; i < respat; i ++) { 39 ll a = rand()%(n-2)+2; 40 ll x = mod_exp(a,d,n); 41 ll y = 0LL; 42 for(int j = 0; j < k; j ++){ 43 y = mod_mul(x,x,n); 44 if(1LL==y && 1LL!=x && n-1LL!=x)return false; 45 x = y; 46 } 47 if(1LL != y) return false; 48 } 49 return true; 50 } 51 52 ll gcd(ll a, ll b) { 53 if(a == 0) return 1; 54 if(a < 0) return gcd(-a,b); 55 while(b) { 56 ll t = a%b; 57 a = b; 58 b = t; 59 } 60 return a; 61 } 62 63 ll Pollard_rho(ll x, ll c) { 64 ll i =1, k=2; 65 ll x0=rand()%x; 66 ll y = x0; 67 while(1) 68 { 69 i++; 70 x0 = (mod_mul(x0,x0,x)+c)%x; 71 ll d = gcd(y-x0,x); 72 if(d!=1 && d!=x) return d; 73 if(y == x0) return x; 74 if(i == k) {y=x0; k+=k;} 75 } 76 } 77 78 void findfac(ll n) { 79 if(n <= 1) return ; 80 if(ispirme(n)) { 81 a[tot++] = n; 82 return; 83 } 84 ll p = n; 85 while(p >= n) 86 p = Pollard_rho(p,rand()%(n-1)+1); 87 findfac(p); 88 findfac(n/p); 89 } 90 91 int main() { 92 ll t, n, ans = 1, cnt = 0; 93 scanf("%lld", &n); 94 if(ispirme(n)) printf("2\n"); 95 else { 96 findfac(n); 97 for(int i = 0; i < tot; i ++) { 98 ll cnt = 0; 99 // printf("%d\n",a[i]); 100 while(n > 0 && n%a[i] == 0) { 101 cnt++; 102 n /= a[i]; 103 } 104 if(cnt) ans *= (cnt+1); 105 } 106 printf("%lld\n",ans); 107 } 108 return 0; 109 }
G Extreme Sort
John likes sorting algorithms very much. He has studied quick sort, merge sort, radix sort, and many more.
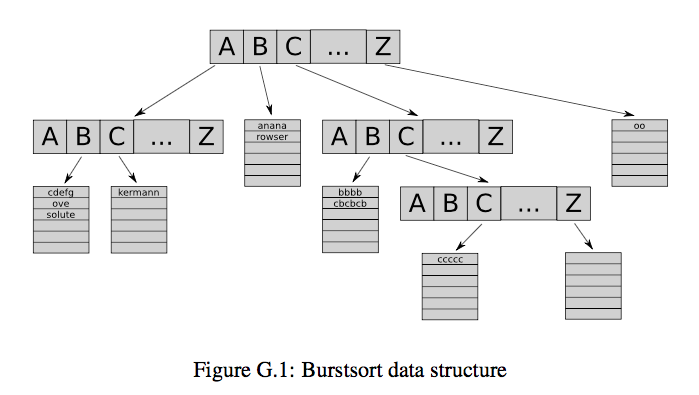
A long time ago he has written a lock-free parallel string sorting program. It was a combination of burst sort and multi-key quick sort. To implement burst sort you need to build a tree of buckets.For each input string you walk through the tree and insert part of the string into the right bucket.When a bucket fills up, it "bursts" and becomes a new subtree (with new buckets).
Well, enough about the past. Today John is playing with sorting algorithms again. This time it’s numbers. He has an idea for a new algorithm, “extreme sort”. It’s extremely fast, performance levels are OVER NINETHOUSAND. Before he tells anyone any details, he wants to make sure that it works correctly.
Your task is to help him and verify that the so-called extreme property holds after the first phase of the algorithm. The extreme property is defined as min (xi,j ) ≥ 0, where
Input
The first line contains a single integer N (1 ≤ N ≤ 1024). The second line contains N integers a1 a2 ... aN (1≤ai≤1024).
Output
Print one line of output containing “yes” if the extreme property holds for the given input, “no”otherwise.
样例输入1
2 1 2
样例输出1
yes
样例输入2
4 2 1 3 4
样例输出2
no
水题。
1 #include <bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 #define ll long long 4 using namespace std; 5 const int N = 1e3+10; 6 int a[N]; 7 int main() { 8 int t, n; 9 cin >> n; 10 for(int i = 1; i <= n; i ++) cin >> a[i]; 11 for(int i = 1; i <= n; i ++) { 12 for(int j = i+1; j <= n; j ++) { 13 if(a[j]-a[i] < 0) return 0*printf("no\n"); 14 } 15 } 16 printf("yes\n"); 17 return 0; 18 }
H Legacy Code
Once again you lost days refactoring code, which never runs in the first place. Enough is enough– your time is better spent writing a tool that finds unused code!
Your software is divided into packages and executables. A package is a collection of methods. Executables are packages defining among other methods exactly one method with namePROGRAM. This method is executed on the start of the corresponding executable. Ordinary packages have no method named PROGRAM.
Each method is uniquely identified by the combination of package and method names. E.g.the method with the identifier SuperGame::PROGRAM would be the main method of the executable SuperGame.
For every method in your software you are given a list of methods directly invoking it. Thus you can easily identify methods, that are never called from any method. However, your task is more challenging: you have to find unused methods. These are methods that are never reached by the control flow of any executable in your software.
Input
The first line of the input contains an integer N, the number of methods in your software(1≤N ≤400).
Each method is described by two lines, totaling in 2 · N lines. The first line consists of the unique identifier of the method and ki, the number of methods directly invoking this one (0 ≤ ki ≤ N).The second line consists of a set of ki identifiers of these calling methods or is empty if there are no such methods, i.e. ki = 0.
Method identifiers consist of a package name followed by two colons and a method name like Packagename::Methodname. Both strings, the package and the method name, each consist of up to 20 lowercase, uppercase characters or digits (a-z, A-Z, 0-9).
There will be exactly N different method identifiers mentioned in the input.
Output
A line containing the number of unused methods in your software.
样例输入1
2 SuperGame::PROGRAM 0 HelpPackage::HelpFunction 2 HelpPackage::HelpFunction SuperGame::PROGRAM
样例输出1
0
样例输入2
2 Loop::CallA 1 Loop::CallB Loop::CallB 1 Loop::CallA
样例输出2
2
每个方法都可以由其他方法调用,带有PROGRAM的是可执行文件,问最要有几个方法没有被执行
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 1010; 4 map<string,int> mp; 5 map<int,string> mp1; 6 vector<int> vs[N]; 7 vector<string> vs1[N]; 8 bool vis[N]; 9 void dfs(int x) { 10 vis[x] = 1; 11 for(int i = 0; i < vs[x].size(); i ++) { 12 if(!vis[vs[x][i]]) { 13 dfs(vs[x][i]); 14 } 15 } 16 } 17 int main() { 18 int n, k; 19 cin >> n; 20 string s; 21 for(int i = 1; i <= n; i ++) { 22 cin >> s; 23 mp[s] = i; 24 mp1[i] = s; 25 cin >> k; 26 for(int j = 0; j < k; j ++) { 27 cin >> s; 28 vs1[i].push_back(s); 29 } 30 } 31 for(int i = 1; i <= n; i ++) { 32 for(int j = 0; j < vs1[i].size(); j ++) { 33 vs[mp[vs1[i][j]]].push_back(i); 34 } 35 } 36 for(int i = 1; i <= n; i ++) { 37 if(mp1[i].find("PROGRAM") != string::npos && !vis[i]) { 38 for(int j = 0; j < vs[i].size(); j ++) { 39 dfs(vs[i][j]); 40 vis[vs[i][j]] = 1; 41 } 42 vis[i] = 1; 43 } 44 } 45 int ans = 0; 46 for(int i =1; i <= n; i ++) { 47 if(!vis[i]) ans++; 48 } 49 cout << ans << endl; 50 return 0; 51 }
I Milling machines
A fab lab is an open, small-scale workshop where you can create or fabricate almost anything you want mostly by using computer controlled tools like a laser cutter or a 3D printer. The FAU fab lab recently got a CNC milling machine. Using the milling machine you can cut or remove material with different tools from the surface of a workpiece. It is controlled via a computer program.
I sometimes wondered what happens if multiple different shaped workpieces are sent through the same milling program. For simplification assume that we have only two dimensional workpieces without holes. A milling program consists of multiple steps; each step describes where the milling machine has to remove material (using different tools) from the top of the surface.
Input
The first line consists of two integers W and S, where W gives the number of workpieces andS the number of steps in the milling program (1 ≤ W, S ≤ 10^4104). The next line consists of two integers X and Y , where X gives the width and Y gives the maximal possible height of workpieces (1 ≤ X, Y ≤ 100).
Then follow W lines, each describing one workpiece. Each workpiece description consists of X non-negative integers specifying the surface height in that column.
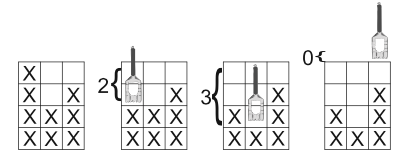
Then follow S lines, each describing one milling step of the milling program. Each milling step description consists of X non-negative integers si (0 ≤ si ≤ Y ) specifying the amount of surface to cut off in each column (relative to the height of the milling area, i.e. Y , not relative to the top of the workpiece). See Fig. I.1 for details.
Output
For each workpiece, output one line containing X integers specifying the remaining surface heights (in the same order as in the input).
Figure I.1: Second workpiece in first sample: initial workpiece followed by milling in each column – the value in the milling program determines the vertical position of the cutter head.
样例输入1
2 1 3 4 4 4 4 4 2 3 2 3 0
样例输出1
2 1 4 2 1 3
样例输入2
1 3 10 100 11 22 33 44 55 66 77 88 99 100 1 100 1 100 1 100 1 100 1 100 58 58 58 58 58 58 58 58 58 58 42 42 42 42 42 42 42 42 66 42
样例输出2
11 0 33 0 42 0 42 0 34 0
水题
1 #include <bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 #define ll long long 4 using namespace std; 5 const int N = 1e4+10; 6 int a[N][101], b[110]; 7 int main() { 8 int w, s, x, y, tmp; 9 cin >> w >>s; 10 cin >> x >> y; 11 for(int i = 1; i <= w; i ++) { 12 for(int j = 1; j <= x; j ++) scanf("%d", &a[i][j]); 13 } 14 for(int i = 1; i <= s; i ++) { 15 for(int j = 1; j <= x; j ++) { 16 scanf("%d", &tmp); 17 b[j] = max(b[j], tmp); 18 } 19 } 20 for(int i = 1; i <= w; i ++) { 21 for(int j = 1; j <= x; j ++) { 22 a[i][j] = min(a[i][j], y-b[j]); 23 printf("%d%c",a[i][j]," \n"[j==x]); 24 } 25 } 26 return 0; 27 }
K Upside down primes
Last night, I must have dropped my alarm clock. When the alarm went off in the morning, it showed 51:80 instead of 08:15. This made me realize that if you rotate a seven segment display like it is used in digital clocks by 180 degrees, some numbers still are numbers after turning them upside down.
As you can see,
My favourite numbers are primes, of course. Your job is to check whether a number is a prime and still a prime when turned upside down.
Input
One line with the integer N in question (1 ≤ N ≤ 10^{16}1016). N will not have leading zeros.
Output
Print one line of output containing “yes” if the number is a prime and still a prime if turned upside down, “no” otherwise.
样例输入1
151
样例输出1
yes
样例输入2
23
样例输出2
no
样例输入3
18115211
样例输出3
no
求一个数是否是素数,180°倒置是否也是素数。
1 #include <bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 #define ll long long 4 using namespace std; 5 const int N = 1e5+10; 6 char str[30]; 7 ll mod_mul(ll a, ll b, ll n){ 8 ll cnt = 0LL; 9 while(b){ 10 if(b&1LL) cnt = (cnt+a)%n; 11 a=(a+a)%n; 12 b >>= 1LL; 13 } 14 return cnt; 15 } 16 ll mod_exp(ll a, ll b, ll n){ 17 ll res = 1LL; 18 while(b){ 19 if(b&1LL) res = mod_mul(res,a,n); 20 a = mod_mul(a,a,n); 21 b >>= 1LL; 22 } 23 return res; 24 } 25 bool ispirme(ll n){ 26 int respat = 5; 27 if(n==2LL || n==3LL || n==5LL || n==7LL || n==11LL) return true; 28 if(n==1 || !(n%2) || !(n%3) || !(n%5) || !(n%7) || !(n%11)) return false; 29 30 int k = 0; 31 ll d = n-1; 32 33 while(!(d&1LL)){ 34 k++; d >>= 1LL; 35 } 36 srand((ll)time(0)); 37 for(int i = 0; i < respat; i ++) { 38 ll a = rand()%(n-2)+2; 39 ll x = mod_exp(a,d,n); 40 ll y = 0LL; 41 for(int j = 0; j < k; j ++){ 42 y = mod_mul(x,x,n); 43 if(1LL==y && 1LL!=x && n-1LL!=x)return false; 44 x = y; 45 } 46 if(1LL != y) return false; 47 } 48 return true; 49 } 50 int main() { 51 ll x = 0, y = 0; 52 cin >> str; 53 int len = strlen(str); 54 for(int i = 0; i < len; i ++) { 55 if(str[i] == '3' || str[i] == '4' || str[i] == '7') return 0*printf("no\n"); 56 x = x*10 + str[i]-'0'; 57 } 58 for(int i = len-1; i >= 0; i --) { 59 ll tmp = str[i] - '0'; 60 if(tmp == 9) tmp = 6; 61 else if(tmp == 6) tmp = 9; 62 y = y*10 + tmp; 63 } 64 // cout << x << ' ' << y << endl; 65 if(ispirme(x) && ispirme(y)) printf("yes\n"); 66 else printf("no\n"); 67 return 0; 68 }