hdu 2256 Problem of Precision

Problem of Precision

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1695    Accepted Submission(s): 1047

Problem Description

 

 

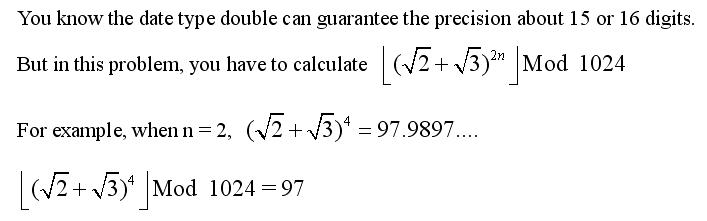
Input

The first line of input gives the number of cases, T. T test cases follow, each on a separate line. Each test case contains one positive integer n. (1 <= n <= 10^9)

 

 

Output

For each input case, you should output the answer in one line.

 

 

Sample Input

3

1

2

5

 

 

Sample Output

9

97

841

 

(√2+√3)²ⁿ = (5+2√6)ⁿ =  x_n + y_n√6 , 即x_n + y_n√6 = (x_n-1 + y_n-1√6)*(5+2√6) = (5x_n-1+12y_n-1)+(5√6y_n-1+2√6x_n-1)

 

由于有根号，浮点求模有误差

同理可得(5+2√6)ⁿ + (5-2√6)ⁿ = 2X_n

(5-2√6)ⁿ < 1

所以(5+2√6)ⁿ = 2X_n-1

(5+26‾√)n+(5−26‾√)n=2A

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 const int mod = 1024;
 4 typedef vector<int> vec;
 5 typedef vector<vec> mat;
 6 
 7 mat mul(mat &A, mat &B) {
 8     mat C(A.size(), vec(B[0].size()));
 9     for(int i = 0; i < A.size(); i ++) {
10         for(int j = 0; j < B[0].size(); j ++) {
11             for(int k = 0; k < B.size(); k ++) {
12                 C[i][j] = (C[i][j] + A[i][k]*B[k][j]);
13             }
14             C[i][j] %= mod;
15         }
16     }
17     return C;
18 }
19 
20 mat pow(mat A, int n) {
21     mat B(A.size(), vec(A[0].size()));
22     for(int i = 0; i < B.size(); i ++) B[i][i] = 1;
23     while(n) {
24         if(n&1) B = mul(A, B);
25         A = mul(A, A);
26         n >>= 1;
27     }
28     return B;
29 }
30 
31 int main() {
32     int t, n;
33     cin >> t;
34     while(t--) {
35         cin >> n;
36         mat A(2, vec(2));
37         A[0][0] = 5; A[0][1] = 12;
38         A[1][0] = 2; A[1][1] = 5;
39         A = pow(A, n-1);
40         // cout << A[0][0]*5+A[0][1]*2 << ' ' << A[1][0]*5+A[1][1]*2 << endl;
41         int ans = (A[0][0]*5+A[0][1]*2)*2-1;
42         cout << ans%mod << endl;
43     }
44     return 0;
45 }