Codeforces Round #465 (Div. 2) ABCD

A. Fafa and his Company

Fafa owns a company that works on huge projects. There are n employees in Fafa's company. Whenever the company has a new project to start working on, Fafa has to divide the tasks of this project among all the employees.

Fafa finds doing this every time is very tiring for him. So, he decided to choose the best l employees in his company as team leaders. Whenever there is a new project, Fafa will divide the tasks among only the team leaders and each team leader will be responsible of some positive number of employees to give them the tasks. To make this process fair for the team leaders, each one of them should be responsible for the same number of employees. Moreover, every employee, who is not a team leader, has to be under the responsibility of exactly one team leader, and no team leader is responsible for another team leader.

Given the number of employees n, find in how many ways Fafa could choose the number of team leaders l in such a way that it is possible to divide employees between them evenly.

Input

The input consists of a single line containing a positive integer n (2 ≤ n ≤ 105) — the number of employees in Fafa's company.

Output

Print a single integer representing the answer to the problem.

Examples

input

Copy

2

output

Copy

1

input

Copy

10

output

Copy

3

Note

In the second sample Fafa has 3 ways:

• choose only 1 employee as a team leader with 9 employees under his responsibility.
• choose 2 employees as team leaders with 4 employees under the responsibility of each of them.
• choose 5 employees as team leaders with 1 employee under the responsibility of each of them.

计算有多少种分法

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 110;
int main() {
    int n, ans = 0;
    cin >> n;
    for(int i = 1; i <= n/2; i ++) {
        if((n-i)%i==0) ans++;
    }
    cout << ans << endl;
    return 0;
}

 

B. Fafa and the Gates

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Two neighboring kingdoms decided to build a wall between them with some gates to enable the citizens to go from one kingdom to another. Each time a citizen passes through a gate, he has to pay one silver coin.

The world can be represented by the first quadrant of a plane and the wall is built along the identity line (i.e. the line with the equation x = y). Any point below the wall belongs to the first kingdom while any point above the wall belongs to the second kingdom. There is a gate at any integer point on the line (i.e. at points (0, 0), (1, 1), (2, 2), ...). The wall and the gates do not belong to any of the kingdoms.

Fafa is at the gate at position (0, 0) and he wants to walk around in the two kingdoms. He knows the sequence S of moves he will do. This sequence is a string where each character represents a move. The two possible moves Fafa will do are 'U' (move one step up, from (x, y)to (x, y + 1)) and 'R' (move one step right, from (x, y) to (x + 1, y)).

Fafa wants to know the number of silver coins he needs to pay to walk around the two kingdoms following the sequence S. Note that if Fafa visits a gate without moving from one kingdom to another, he pays no silver coins. Also assume that he doesn't pay at the gate at point (0, 0), i. e. he is initially on the side he needs.

Input

The first line of the input contains single integer n (1 ≤ n ≤ 105) — the number of moves in the walking sequence.

The second line contains a string S of length n consisting of the characters 'U' and 'R' describing the required moves. Fafa will follow the sequence S in order from left to right.

Output

On a single line, print one integer representing the number of silver coins Fafa needs to pay at the gates to follow the sequence S.

Examples

input

Copy

1
U

output

Copy

0

input

Copy

6
RURUUR

output

Copy

1

input

Copy

7
URRRUUU

output

Copy

2

Note

The figure below describes the third sample. The red arrows represent the sequence of moves Fafa will follow. The green gates represent the gates at which Fafa have to pay silver coins.

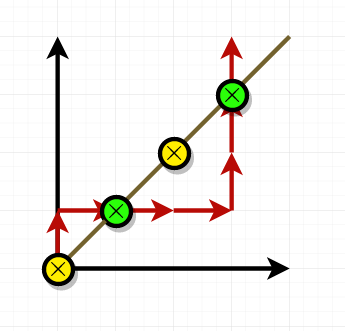
模拟题

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+10;
char str[N];
int main() {
    int n, ans = 0, flag = -1, x = 0, y = 0;
    cin >> n >> str;
    for(int i = 0; i < n; i ++) {
        if(str[i] == 'U') {
            y++;
            if(i == 0) flag = 1;
            if(y > x && flag == 2) {
                ans++;
                flag = 1;
            }
        } else{
            x++;
            if(i == 0) flag = 2;
            if(x > y && flag == 1) {
                ans++;
                flag = 2;
            }
        }
    }
    cout << ans << endl;
    return 0;
}

 

C. Fifa and Fafa

Fifa and Fafa are sharing a flat. Fifa loves video games and wants to download a new soccer game. Unfortunately, Fafa heavily uses the internet which consumes the quota. Fifa can access the internet through his Wi-Fi access point. This access point can be accessed within a range of r meters (this range can be chosen by Fifa) from its position. Fifa must put the access point inside the flat which has a circular shape of radius R. Fifa wants to minimize the area that is not covered by the access point inside the flat without letting Fafa or anyone outside the flat to get access to the internet.

The world is represented as an infinite 2D plane. The flat is centered at (x1, y1) and has radius R and Fafa's laptop is located at (x2, y2), not necessarily inside the flat. Find the position and the radius chosen by Fifa for his access point which minimizes the uncovered area.

Input

The single line of the input contains 5 space-separated integers R, x1, y1, x2, y2 (1 ≤ R ≤ 105, |x1|, |y1|, |x2|, |y2| ≤ 105).

Output

Print three space-separated numbers xap, yap, r where (xap, yap) is the position which Fifa chose for the access point and r is the radius of its range.

Your answer will be considered correct if the radius does not differ from optimal more than 10 - 6 absolutely or relatively, and also the radius you printed can be changed by no more than 10 - 6 (absolutely or relatively) in such a way that all points outside the flat and Fafa's laptop position are outside circle of the access point range.

Examples

input

Copy

5 3 3 1 1

output

Copy

3.7677669529663684 3.7677669529663684 3.914213562373095

input

Copy

10 5 5 5 15

output

Copy

5.0 5.0 10.0

 

几何题。给定一个圆和点，在圆内求一内圈是的点不在内圆内，且内圆占圆的面积最大。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 110;
double dis(double x1, double y1, double x2, double y2) {
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
int main() {
    double r, x1, x2, y1, y2;
    cin >> r >> x1 >> y1 >> x2 >> y2;
    if(dis(x1,y1,x2,y2) >= r) {
        printf("%lf %lf %lf\n",x1,y1,r);
    } else if(x1 == x2 && y1 == y2){
        printf("%lf %lf %lf\n",x1,y1+r/2,r/2);
    }else{
        double d = dis(x1,y1,x2,y2);
        double R = (r+d)/2;
        printf("%lf %lf %lf\n",x2+(x1-x2)*R/d,y2+(y1-y2)*R/d,R);
    }
    return 0;
}

D. Fafa and Ancient Alphabet

Ancient Egyptians are known to have used a large set of symbols  to write on the walls of the temples. Fafa and Fifa went to one of the temples and found two non-empty words S1 and S2 of equal lengths on the wall of temple written one below the other. Since this temple is very ancient, some symbols from the words were erased. The symbols in the set  have equal probability for being in the position of any erased symbol.

Fifa challenged Fafa to calculate the probability that S1 is lexicographically greater than S2. Can you help Fafa with this task?

You know that 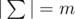, i. e. there were m distinct characters in Egyptians' alphabet, in this problem these characters are denoted by integers from 1 to m in alphabet order. A word x is lexicographically greater than a word y of the same length, if the words are same up to some position, and then the word x has a larger character, than the word y.

We can prove that the probability equals to some fraction 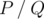, where P and Q are coprime integers, and 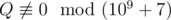. Print as the answer the value 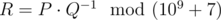, i. e. such a non-negative integer less than 109 + 7, such that 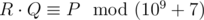, where  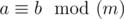means that a and b give the same remainders when divided by m.

Input

The first line contains two integers n and m (1 ≤ n,  m ≤ 105) — the length of each of the two words and the size of the alphabet 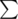, respectively.

The second line contains n integers a1, a2, ..., an (0 ≤ ai ≤ m) — the symbols of S1. If ai = 0, then the symbol at position i was erased.

The third line contains n integers representing S2 with the same format as S1.

Output

Print the value 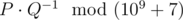, where P and Q are coprime and  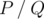is the answer to the problem.

Examples

input

Copy

1 2
0
1

output

Copy

500000004

input

Copy

1 2
1
0

output

Copy

0

input

Copy

7 26
0 15 12 9 13 0 14
11 1 0 13 15 12 0

output

Copy

230769233

Note

In the first sample, the first word can be converted into (1) or (2). The second option is the only one that will make it lexicographically larger than the second word. So, the answer to the problem will be 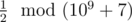, that is 500000004, because .

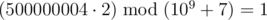In the second example, there is no replacement for the zero in the second word that will make the first one lexicographically larger. So, the answer to the problem is 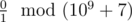, that is 0.

 

概率+逆元。

两个字符串，求a>b的概率是多少。数字0表示可以变成1-m中的其中一个数字。

四种情况：

1、都不为0，ai>bi的话概率就用之前的。

2、ai为0，bi不为0，概率就是p*(m-b[i)/m

3、ai不为0，bi为0，概率就是p*(ai-1)/m

4、都为0，概率是p*(m-1)/2*m

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 1e9+7;
const int N = 1e5+10;
ll a[N], b[N];
ll pow_mod(ll x, ll n){
    ll res=1;
    while(n>0){
        if(n&1)res=res*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return res;
}
int main() {
    ll n, m, p = 1, ans = 0;
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i <= n; i ++) cin >> b[i];
    for(int i = 1; i <= n; i ++) {
        if(a[i]&&b[i]) {
            if(a[i] > b[i]) {
                ans += p;
                ans %= mod;
                break;
            } else if(a[i] < b[i])break;
        } else if(a[i]&&!b[i]){
            ans += p*(a[i]-1LL)%mod*pow_mod(m,mod-2);
            ans %= mod;
            p *= pow_mod(m,mod-2);
            p %= mod;
        } else if(!a[i]&&b[i]) {
            ans += p*(m-b[i])%mod*pow_mod(m,mod-2);
            ans %= mod;
            p *= pow_mod(m,mod-2);
            p %= mod;
        } else{
            ans += p*(m-1)%mod*pow_mod(2*m,mod-2);
            ans %= mod;
            p *= pow_mod(m,mod-2);
            p %= mod;
        }
        // cout << ans << endl;
    }
    cout << ans << endl;
    return 0;
}