ICM Technex 2018 and Codeforces Round #463 ABC

A. Palindromic Supersequence

 

You are given a string A. Find a string B, where B is a palindrome and A is a subsequence of B.

A subsequence of a string is a string that can be derived from it by deleting some (not necessarily consecutive) characters without changing the order of the remaining characters. For example, "cotst" is a subsequence of "contest".

A palindrome is a string that reads the same forward or backward.

The length of string B should be at most 104. It is guaranteed that there always exists such string.

You do not need to find the shortest answer, the only restriction is that the length of string B should not exceed 104.

Input

First line contains a string A (1 ≤ |A| ≤ 103) consisting of lowercase Latin letters, where |A| is a length of A.

Output

Output single line containing B consisting of only lowercase Latin letters. You do not need to find the shortest answer, the only restriction is that the length of string B should not exceed 104. If there are many possible B, print any of them.

Examples

input

Copy

aba

output

Copy

aba

input

Copy

ab

output

Copy

aabaa

Note

In the first example, "aba" is a subsequence of "aba" which is a palindrome.

In the second example, "ab" is a subsequence of "aabaa" which is a palindrome.

 

 s+reverse(s)

#include <bits/stdc++.h>
using namespace std;
char str[1010];
int main() {
    cin >> str;
    int len = strlen(str);
    cout << str;
    for(int i = len-1; i >= 0; i --) cout << str[i];
    cout << endl;
    return 0;
}

 

B. Recursive Queries

 

Let us define two functions f and g on positive integer numbers.

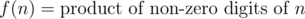
You need to process Q queries. In each query, you will be given three integers l, r and k. You need to print the number of integers xbetween l and r inclusive, such that g(x) = k.

Input

The first line of the input contains an integer Q (1 ≤ Q ≤ 2 × 105) representing the number of queries.

Q lines follow, each of which contains 3 integers l, r and k (1 ≤ l ≤ r ≤ 106, 1 ≤ k ≤ 9).

Output

For each query, print a single line containing the answer for that query.

Examples

input

Copy

4
22 73 9
45 64 6
47 55 7
2 62 4

output

Copy

1
4
0
8

input

Copy

4
82 94 6
56 67 4
28 59 9
39 74 4

output

Copy

3
1
1
5

Note

In the first example:

• g(33) = 9 as g(33) = g(3 × 3) = g(9) = 9
• g(47) = g(48) = g(60) = g(61) = 6
• There are no such integers between 47 and 55.
• g(4) = g(14) = g(22) = g(27) = g(39) = g(40) = g(41) = g(58) = 4

 dfs预处理1e6，然后查询的话就直接查询了。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int g[N], vis[N][10];
int dfs(int x) {
    if(x < 10) return x;
    int ans = 1, tmp = x;
    while(tmp) {
        if(tmp%10) ans *= tmp%10;
        tmp /= 10;
    }
    g[x] = ans>=10?dfs(ans):ans;
    return g[x];
}
int main() {
    for(int i = 1; i <= N; i ++) {
        if(!g[i]) g[i] = dfs(i);
    }
    for(int i = 1; i <= N; i ++) {
        for(int j = 1; j < 10; j ++) {
            vis[i][j] = vis[i-1][j] + (j==g[i]);
        }
    }
    int q, l, r, k;
    cin >> q;
    while(q--) {
        cin >> l >> r >> k;
        cout << vis[r][k] - vis[l-1][k] << endl;
    }
    return 0;
}

C. Permutation Cycle

For a permutation P[1... N] of integers from 1 to N, function f is defined as follows:

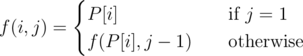
Let g(i) be the minimum positive integer j such that f(i, j) = i. We can show such j always exists.

For given N, A, B, find a permutation P of integers from 1 to N such that for 1 ≤ i ≤ N, g(i) equals either A or B.

Input

The only line contains three integers N, A, B (1 ≤ N ≤ 106, 1 ≤ A, B ≤ N).

Output

If no such permutation exists, output -1. Otherwise, output a permutation of integers from 1 to N.

Examples

input

Copy

9 2 5

output

Copy

6 5 8 3 4 1 9 2 7

input

Copy

3 2 1

output

Copy

1 2 3 

Note

In the first example, g(1) = g(6) = g(7) = g(9) = 2 and g(2) = g(3) = g(4) = g(5) = g(8) = 5

In the second example, g(1) = g(2) = g(3) = 1

 

 求循环节。只要有存在ax+by=n就不是-1，然后按a、b的循环。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int p[N];
int main() {
    int n, a, b, x, y;
    cin >> n >> a >> b;
    for(x = 0; x <= n; x ++) {
        int ans = n-x*a;
        if(ans < 0) break;
        if(ans >= 0 && ans%b==0) {
            y = ans/b;
            break;
        }
    }
    if(x*a > n) printf("-1\n");
    else{
        for(int i = 0; i < x; i ++) {
            p[i*a+1] = (i+1)*a;
            for(int j = i*a+2; j <= (i+1)*a; j ++) {
                p[j] = j-1;
            }
        }
        for(int i = 0; i < y; i ++) {
            p[a*x+i*b+1] = (i+1)*b+a*x;
            for(int j = x*a+i*b+2; j <= (i+1)*b+a*x; j ++) {
                p[j] = j-1;
            }
        }
        for(int i = 1; i <= n; i ++) {
            printf("%d ",p[i]);
        }
    }
    return 0;
}