Codeforces Round #461 (Div. 2) ABC

A. Cloning Toys

Recently, he found a machine that can clone plush toys. Imp knows that if he applies the machine to an original toy, he additionally gets one more original toy and one copy, and if he applies the machine to a copied toy, he gets two additional copies.

Initially, Imp has only one original toy. He wants to know if it is possible to use machine to get exactly x copied toys and y original toys? He can't throw toys away, and he can't apply the machine to a copy if he doesn't currently have any copies.

Input

The only line contains two integers x and y (0 ≤ x, y ≤ 109) — the number of copies and the number of original toys Imp wants to get (including the initial one).

Output

Print "Yes", if the desired configuration is possible, and "No" otherwise.

You can print each letter in arbitrary case (upper or lower).

Examples

input

Copy

6 3

output

Copy

Yes

input

Copy

4 2

output

Copy

No

input

Copy

1000 1001

output

Copy

Yes

Note

In the first example, Imp has to apply the machine twice to original toys and then twice to copies.

 

初始x = 0, y = 1,用1个y可以得到1个x和1个y，用1个x可以得到2个x，问给定的(x,y)是否可以根据给定的规则得到。

#include <bits/stdc++.h>
using namespace std;

int main() {
	int x, y;
	cin >> x >>y;
	if(y==0||(y==1&&x)||x<y-1||(x-y)%2==0)printf("No\n");
	else printf("Yes\n");
	return 0;
}

　　

B. Magic Forest

Imp is in a magic forest, where xorangles grow (wut?)

A xorangle of order n is such a non-degenerate triangle, that lengths of its sides are integers not exceeding n, and the xor-sum of the lengths is equal to zero. Imp has to count the number of distinct xorangles of order n to get out of the forest.

Formally, for a given integer n you have to find the number of such triples (a, b, c), that:

• 1 ≤ a ≤ b ≤ c ≤ n;
• , where 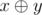 denotes the bitwise xor of integers x and y.
• (a, b, c) form a non-degenerate (with strictly positive area) triangle.

Input

The only line contains a single integer n (1 ≤ n ≤ 2500).

Output

Print the number of xorangles of order n.

Examples

input

Copy

6

output

Copy

1

input

Copy

10

output

Copy

2

Note

The only xorangle in the first sample is (3, 5, 6).

 

 为是否有这样的三角形边满足i^j^k等于0，只要得到i^j  满足x [j,n]且能构成三角形即可

#include <bits/stdc++.h>
using namespace std;

int main() {
	int n, ans = 0;
	cin >> n;
	for(int i = 1; i <= n; i ++) {
		for(int j = i; j <= n; j ++) {
			int x = i^j;
			if(x >= j && i+j > x && x <= n) ans++;
		}
	}
	cout << ans<<endl;
	return 0;
}

　　

C. Cave Painting

Imp is watching a documentary about cave painting.

Some numbers, carved in chaotic order, immediately attracted his attention. Imp rapidly proposed a guess that they are the remainders of division of a number n by all integers i from 1 to k. Unfortunately, there are too many integers to analyze for Imp.

Imp wants you to check whether all these remainders are distinct. Formally, he wants to check, if all 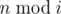, 1 ≤ i ≤ k, are distinct, i. e. there is no such pair (i, j) that:

• 1 ≤ i < j ≤ k,
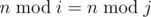• , where  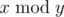is the remainder of division x by y.

Input

The only line contains two integers n, k (1 ≤ n, k ≤ 1018).

Output

Print "Yes", if all the remainders are distinct, and "No" otherwise.

You can print each letter in arbitrary case (lower or upper).

Examples

input

Copy

4 4

output

Copy

No

input

Copy

5 3

output

Copy

Yes

Note

In the first sample remainders modulo 1 and 4 coincide.

 

 给定n，k。求n%1,n%2...n%k  是否是k个不同的数，是就是yes，否则就是no。

n%1 = 0,n%2 = (0|1)

由于n%1=0,所以n%2一定要等于1才行,n%3=(0|1|2) 所以一定要等于2

即n%i = i-1才行，有一个不成立就是No

#include <bits/stdc++.h>
using namespace std;
#define ll long long
int main() {
	ll n, k;
	cin >> n >> k;
	bool flag = true;
	for(ll i = 1; i <= k; i ++) {
		if(n%i != i-1) {
			flag = false;
			break;
		}
	}
	if(flag) printf("Yes\n");
	else printf("No\n");
	return 0;
}