Codeforces Round #453 (Div. 2) ABC
Pig is visiting a friend.
Pig's house is located at point 0, and his friend's house is located at point m on an axis.
Pig can use teleports to move along the axis.
To use a teleport, Pig should come to a certain point (where the teleport is located) and choose where to move: for each teleport there is the rightmost point it can move Pig to, this point is known as the limit of the teleport.
Formally, a teleport located at point x with limit y can move Pig from point x to any point within the segment [x; y], including the bounds.
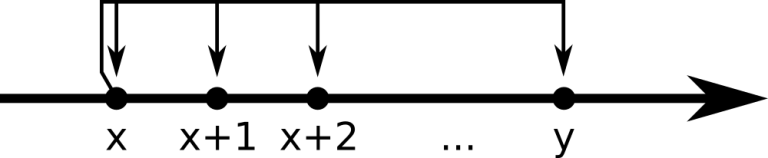
Determine if Pig can visit the friend using teleports only, or he should use his car.
The first line contains two integers n and m (1 ≤ n ≤ 100, 1 ≤ m ≤ 100) — the number of teleports and the location of the friend's house.
The next n lines contain information about teleports.
The i-th of these lines contains two integers ai and bi (0 ≤ ai ≤ bi ≤ m), where ai is the location of the i-th teleport, and bi is its limit.
It is guaranteed that ai ≥ ai - 1 for every i (2 ≤ i ≤ n).
Print "YES" if there is a path from Pig's house to his friend's house that uses only teleports, and "NO" otherwise.
You can print each letter in arbitrary case (upper or lower).
3 5
0 2
2 4
3 5
YES
3 7
0 4
2 5
6 7
NO
The first example is shown on the picture below:
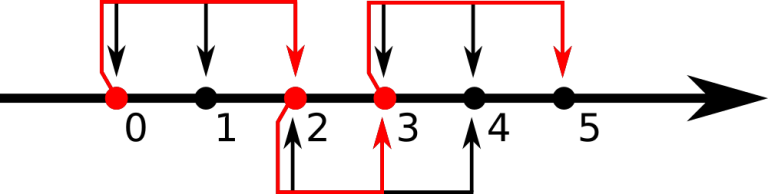
Pig can use the first teleport from his house (point 0) to reach point 2, then using the second teleport go from point 2 to point 3, then using the third teleport go from point 3 to point 5, where his friend lives.
The second example is shown on the picture below:
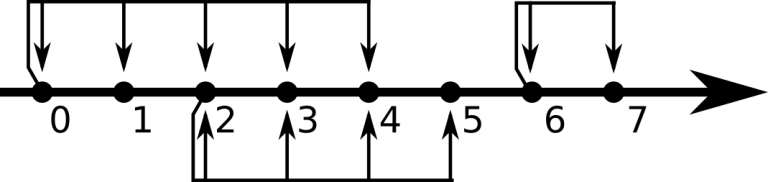
You can see that there is no path from Pig's house to his friend's house that uses only teleports.
问是否可以从0传送到m n个[x,y] 代表可以从x+i 传送到x+j (0<= i <= j <= y-x)边界可以走
1 n, m = map(int,input().split()) 2 l = 0 3 for i in range(n): 4 x,y = map(int, input().split()) 5 if l >= x and l <= y: 6 l = y 7 print(["NO","YES"][l >= m])
You are given a rooted tree with n vertices. The vertices are numbered from 1 to n, the root is the vertex number 1.
Each vertex has a color, let's denote the color of vertex v by cv. Initially cv = 0.
You have to color the tree into the given colors using the smallest possible number of steps. On each step you can choose a vertex v and a color x, and then color all vectices in the subtree of v (including v itself) in color x. In other words, for every vertex u, such that the path from root to u passes through v, set cu = x.
It is guaranteed that you have to color each vertex in a color different from 0.
You can learn what a rooted tree is using the link: https://en.wikipedia.org/wiki/Tree_(graph_theory).
The first line contains a single integer n (2 ≤ n ≤ 104) — the number of vertices in the tree.
The second line contains n - 1 integers p2, p3, ..., pn (1 ≤ pi < i), where pi means that there is an edge between vertices i and pi.
The third line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ n), where ci is the color you should color the i-th vertex into.
It is guaranteed that the given graph is a tree.
Print a single integer — the minimum number of steps you have to perform to color the tree into given colors.
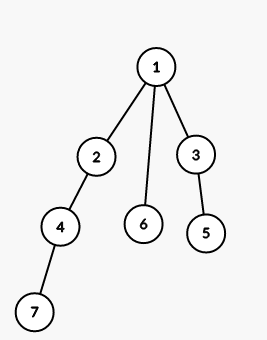
6
1 2 2 1 5
2 1 1 1 1 1
3
7
1 1 2 3 1 4
3 3 1 1 1 2 3
5
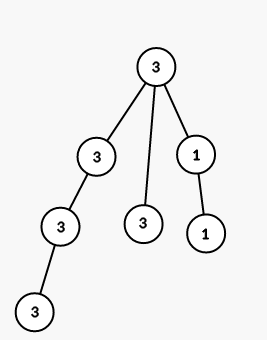
The tree from the first sample is shown on the picture (numbers are vetices' indices):
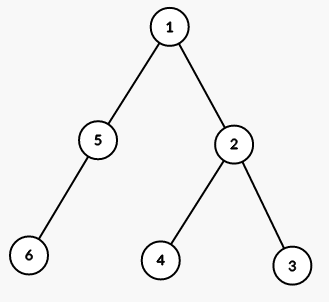
On first step we color all vertices in the subtree of vertex 1 into color 2 (numbers are colors):
On seond step we color all vertices in the subtree of vertex 5 into color 1:

On third step we color all vertices in the subtree of vertex 2 into color 1:
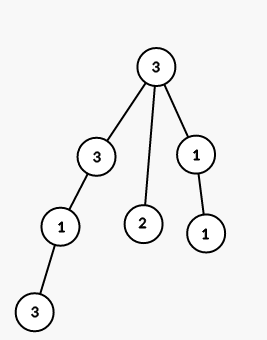
The tree from the second sample is shown on the picture (numbers are vetices' indices):
On first step we color all vertices in the subtree of vertex 1 into color 3 (numbers are colors):
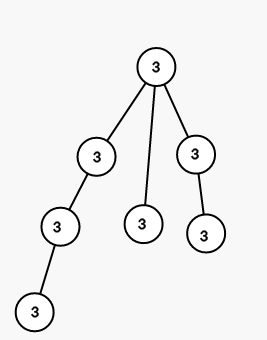
On second step we color all vertices in the subtree of vertex 3 into color 1:
On third step we color all vertices in the subtree of vertex 6 into color 2:

On fourth step we color all vertices in the subtree of vertex 4 into color 1:

On fith step we color all vertices in the subtree of vertex 7 into color 3:
n个定点,pi表示i与pi相连,可以看成i的父亲节点是pi,ci表示i的颜色是i,每一步都看x及x的子节点全部变成一个颜色,所以值要判断定点i与i的父亲节点是否相同就行。
不同的话步骤就要加1了
1 n = int(input()) 2 fa = list(map(int,input().split())) 3 c = list(map(int,input().split())) 4 ans = 1 5 for i in range(n-1): 6 if c[i+1] != c[fa[i]-1]: 7 ans += 1 8 print(ans)
Sasha is taking part in a programming competition. In one of the problems she should check if some rooted trees are isomorphic or not. She has never seen this problem before, but, being an experienced participant, she guessed that she should match trees to some sequences and then compare these sequences instead of trees. Sasha wants to match each tree with a sequence a0, a1, ..., ah, where his the height of the tree, and ai equals to the number of vertices that are at distance of i edges from root.
Unfortunately, this time Sasha's intuition was wrong, and there could be several trees matching the same sequence. To show it, you need to write a program that, given the sequence ai, builds two non-isomorphic rooted trees that match that sequence, or determines that there is only one such tree.
Two rooted trees are isomorphic, if you can reenumerate the vertices of the first one in such a way, that the index of the root becomes equal the index of the root of the second tree, and these two trees become equal.
The height of a rooted tree is the maximum number of edges on a path from the root to any other vertex.
The first line contains a single integer h (2 ≤ h ≤ 105) — the height of the tree.
The second line contains h + 1 integers — the sequence a0, a1, ..., ah (1 ≤ ai ≤ 2·105). The sum of all ai does not exceed 2·105. It is guaranteed that there is at least one tree matching this sequence.
If there is only one tree matching this sequence, print "perfect".
Otherwise print "ambiguous" in the first line. In the second and in the third line print descriptions of two trees in the following format: in one line print 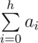 integers, the k-th of them should be the parent of vertex k or be equal to zero, if the k-th vertex is the root.
integers, the k-th of them should be the parent of vertex k or be equal to zero, if the k-th vertex is the root.
These treese should be non-isomorphic and should match the given sequence.
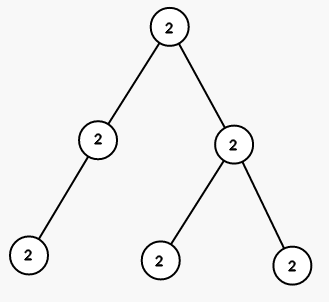
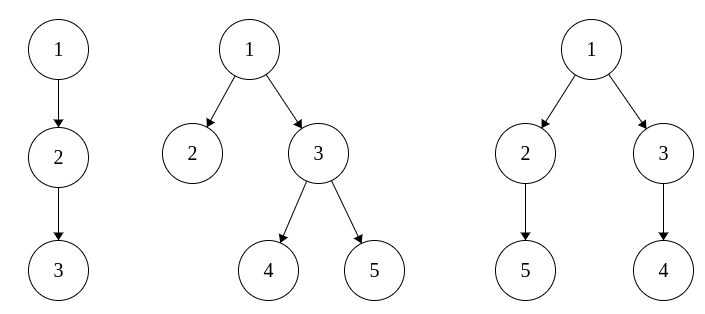
2
1 1 1
perfect
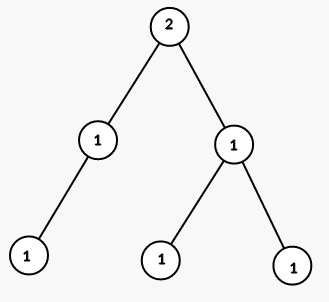
2
1 2 2
ambiguous
0 1 1 3 3
0 1 1 3 2
The only tree in the first example and the two printed trees from the second example are shown on the picture:
求是否存在同构,存在同构的条件是第i层和第i-1层的节点数都大于1就存在,我们可以把第i层的所以父亲节点都当作上一层的最后一个节点,当存在同构时,就把其中一个节点的父亲节点当做上一层的倒数第二个节点。这样遍历下去就可以了。
1 h = int(input()) 2 a = list(map(int,input().split())) 3 p, c, f = 0, 0, False 4 s1, s2 = [], [] 5 for i in a: 6 for j in range(i): 7 s1.append(c) 8 if not f and p >= 2 and i >= 2: 9 f = True 10 s2.append(c-1) 11 else : 12 s2.append(c) 13 c += i 14 p = i 15 print('perfect' if not f else 'ambiguous') 16 if f: 17 print(*s1) 18 print(*s2)


