2017 Multi-University Training Contest - Team 5 1006 Rikka with Graph

 题目链接http://acm.hdu.edu.cn/showproblem.php?pid=6090

Problem Description

As we know, Rikka is poor at math. Yuta is worrying about this situation, so he gives Rikka some math tasks to practice. There is one of them:

For an undirected graph G with n nodes and m edges, we can define the distance between (i,j) (dist(i,j)) as the length of the shortest path between i and j. The length of a path is equal to the number of the edges on it. Specially, if there are no path between i and j, we make dist(i,j) equal to n.

Then, we can define the weight of the graph G (wG) as ∑ni=1∑nj=1dist(i,j).

Now, Yuta has n nodes, and he wants to choose no more than m pairs of nodes (i,j)(i≠j) and then link edges between each pair. In this way, he can get an undirected graph G with n nodes and no more than m edges.

Yuta wants to know the minimal value of wG.

It is too difficult for Rikka. Can you help her?  

In the sample, Yuta can choose (1,2),(1,4),(2,4),(2,3),(3,4).

 

 

Input

The first line contains a number t(1≤t≤10), the number of the testcases.

For each testcase, the first line contains two numbers n,m(1≤n≤106,1≤m≤1012).

 

 

Output

For each testcase, print a single line with a single number -- the answer.

 

 

Sample Input

1 4 5

 

 

Sample Output

14

 

 

找规律。其实可以让1连接其他所有的点，当m = n -1时，比如n = 6， m = 5。可以这样连，1到所以的点都是1，其他的点除了到1的距离是1的话都是2。

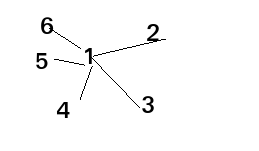
1、m  <= n-1时，假设有x个点没有连接任何点，1连接的是 m + x*n ,其他m个连接1的点都是1+2*(m-1)+x*n ,x个没有连接的点都是 n*(n-1)。所以答案是m+x*n+m*(1+2*(m-1)+x*n)+x*n*(n-1)，化简就是2*m*m+x*n*m+x*n*n。

2、n - 1 < m < n*(n-1)/2是就好办了，就是2*(n-1)*(n-1) - 2 * x

3、m >= n*(n-1)/2 就是n*(n-1)。

 

#include <iostream>
#include <stdio.h>
#include <string.h>
#define ll long long
using namespace std;

int main() {
    int t;
    scanf("%d", &t);
    while(t--) {
        ll n, m;
        scanf("%lld %lld", &n, &m);
        if(m <= n-1) {
            ll x = n-1-m;
            printf("%lld\n",2*m*m+x*n*m+x*n*n);
        } else if(m >= n*(n-1)/2) {
            printf("%lld\n",n*(n-1));
        } else {
            ll x = m - n + 1;
            printf("%lld\n",2*(n-1)*(n-1) - 2 * x);
        }
    }
    return 0;
}