并查集（初步）

并查集可以查询某个是否在一个集合里，而且可以把两个或以上的集合合并起来。

比如有三个集合{1, 3, 5, 7, 9}, {2, 4, 6, 8, 10}, {11, 12, 13, 14},其中1和5在一个集合里2和11不在一个集合里。

经典的题目：n个人，有m对关系，如果a和b是亲戚，b和c是亲戚，则a和c也是亲戚，求有多少组亲戚。描述的不是很好，看例子吧。假设有5个人，1和2是亲戚，2和3是亲戚，4和5是亲戚。那么答案是2，因为亲戚组有两组，分别是{1, 2, 3}，{4, 5}。

树关系如下

 

在查询两个人是否是亲戚时，最要查询他们最终的根是否相同即可，比如查询1和3是否是亲戚，因为1的最终根是1,3的最终根也是1，所以1和3是亲戚。

当然，层数很多时速度很慢，那我们就可以把路径压缩下了。

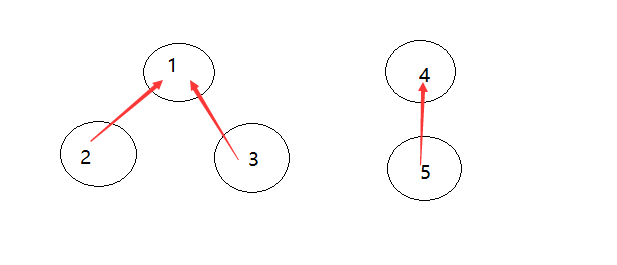
这样从3查询最终的根只要查询一次，之前要查询两次，但层数很多时，用路径压缩的速度可快了很多。

下面写下主要的代码：

int find(int x){
    if(fa[x] == x)return x;
    else return fa[x] = find(fa[x]);
}
void uni(int x, int y){
    x = find(x);
    y = find(y);
    if(x == y)return;
    if(x < y){
        fa[x] = y;
    }else{
        fa[y] = x;
    }
}

其中fa[i] 表示i的父亲，第三行实现了路径压缩。

下面给出一个标准的并查集题目:

畅通工程

某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？ 

Input

测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。 
注意:两个城市之间可以有多条道路相通,也就是说 
3 3 
1 2 
1 2 
2 1 
这种输入也是合法的 
当N为0时，输入结束，该用例不被处理。 
Output

对每个测试用例，在1行里输出最少还需要建设的道路数目。 
Sample Input

4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0

Sample Output

1
0
2
998


        
 
Huge input, scanf is recommended.

题意是求把所有的道路直接或间接的连接，最少需要修多少条道路。
代码如下：

#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 1e3+10;
int fa[maxn];
int n, m;
int find(int x){
    if(fa[x] == x)return x;
    else return fa[x] = find(fa[x]);
}
void uni(int x, int y){
    x = find(x);
    y = find(y);
    if(x == y)return;
    if(x < y){
        fa[x] = y;
    }else{
        fa[y] = x;
    }
}
int main(){
    int a, b;
    while(~scanf("%d",&n)){
        if(n == 0)break;
        scanf("%d",&m);
        int ans = 0;
        for(int i = 1; i <= n; i ++) {
            fa[i] = i;
        }
        for(int i = 1; i <= m; i ++){
            scanf("%d%d",&a,&b);
            uni(a,b);
        }
        for(int i = 1; i <= n; i ++){
            if(fa[i] == i) ans++;
        }
        cout << ans - 1 << endl;
    }
    return 0;
}