递归学习

今天学长教了递归，下面说说我对递归的一些理解。

 

以下面这个题目为例：

题目描述

Ø例5.2 求Fibonacci数列问题。
─斐波那契数列指的是这样一个数列：
─0、1、1、2、3、5、8、13、21、……
─F[0]=0, F[1]=1, F[i]=F[i-1]+F[i-2], i>=2;
编程输出前n个Fibonacci数

输入

输入n

输出

输出前n个Fibonacci数

样例输入

5

样例输出

0
1
1
2
3


当求F[5]时，它们的层数关系如下：

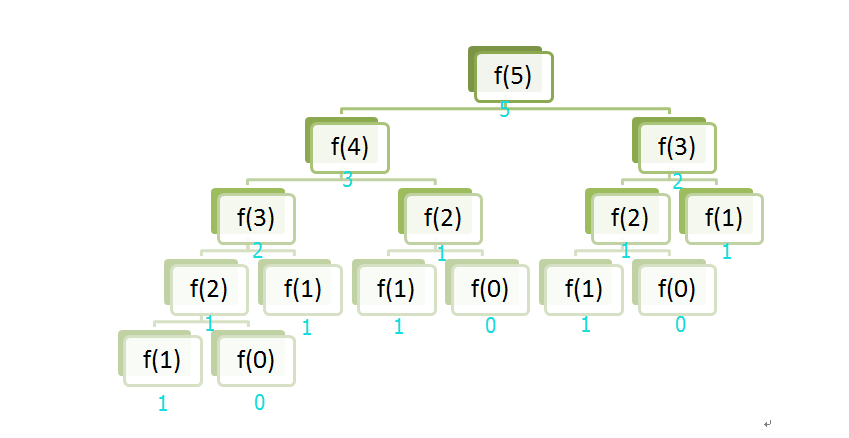
求F[5]时就要知道F[4]和F[3]的值，而F[4]的值等于F[3]+F[2]，F[3]的值等于F[2]+F[1]，依次递归下去，由于F[1]和F[0]的值知道，所以直到等于F[1]或F[0]时递归结束。

 

具体代码如下：

 

#include <iostream>
using namespace std;
 
int f(int x){
    if(x == 0){
        return 0;
    }
    else if(x == 1){
      return 1;
    }
    else return f(x-1)+f(x-2);
}
int main(){
    int n;
    cin >> n;
    for(int i = 0; i < n; i++){
        cout << f(i) << endl;
    }
    return 0;
}

 

类似的递归问题还有：

题目描述

对1~ n 的 n个整数进行全排列(n<=9),编写程序输出所有可能的排列组合. 用递归算法实现.

输入

输入n

输出

输入n个整数的所有可能的排列组合.

样例输入

3

样例输出

   1   2   3
   1   3   2
   2   1   3
   2   3   1
   3   2   1
   3   1   2

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
void f(int arr[], int k, int m){
    if(k == m){
        for(int i = 0; i <= m; i++){
            printf("%4d",arr[i]);
        }
        printf("\n");
    }
    else{
        for(int i = k; i <= m; i++){
            swap(arr[i], arr[k]);
            f(arr, k+1, m);
            swap(arr[i], arr[k]);
        }
    }
}
int main(){
    int n;
    cin >> n;
    int a[11];
    for(int i = 0; i < n; i++)
        a[i] = i+1;
    f(a,0,n-1);
    return 0;
}

 

 

题目描述

汉诺（Hanoi）塔问题：古代有一个梵塔，塔内有三个座A、B、C，A座上有n个盘子，盘子大小不等，大的在下，小的在上（如图）。有一个和尚想把这n个盘子从A座移到C座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，小盘在上。在移动过程中可以利用B座，要求打印移动的步骤。如果只有一个盘子，则不需要利用B座，直接将盘子从A移动到C。

输入

输入盘子个数n

输出

输出盘子最少移动的步骤

样例输入

3

样例输出

1:A->C
2:A->B
3:C->B
4:A->C
5:B->A
6:B->C
7:A->C

#include <iostream>
#include <cstdio>
using namespace std;
void move(char x, char y);
void f(int n, char a, char b, char c){
    if(n == 1)
        move(a, c);
    else{
        f(n-1,a,c,b);
        move(a,c);
        f(n-1,b,a,c);
    }
}
void move(char x, char y){
    static int i = 1;
    printf("%d:%c->%c\n",i++,x,y);
}
int main(){
    int n;
    cin >> n;
    f(n, 'A', 'B','C');
    return 0;
}

 

题目描述

八皇后问题
是一个古老而著名的问题，是回溯算法的典型案例。
该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出的，在8*8格的国际象棋上摆放八个皇后;使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上;
问有多少种摆法, 输出所有可能的解？

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const int N = 8;
int a[N][N] = {0};
void Print(){
    static int ans = 1;
    printf("Case %d:\n",ans++);
    for(int i = 0; i < N; i++){
        for(int j = 0; j < N; j++){
            printf("%c ",a[i][j]?'Q':'.');
        }
        printf("\n");
    }
    printf("\n");
}
bool Safety(int row, int col){
    for(int i = 0; i < row; i++){
        for(int j = 0; j < N; j++){
            if(a[i][j]&&(j==col||abs(row-i)==abs(col-j)))
                return false;
        }
    }
    return true;
}
void BlackTrack(int i){
    if(i >= N){
        Print();
        return;
    }
    else{
        for(int j = 0; j < N; j++){
            a[i][j] = 1;
            if(Safety(i,j)){
                BlackTrack(i+1);
            }
            a[i][j] = 0;
        }
    }
}
int main(){
    BlackTrack(0);
    return 0;
}

 

 

输入

没有输入

输出

输出所有可能的解