Weekly Contest 196
周赛地址(英):weekly contest 196
周赛地址(中):第 196 场周赛
仓库地址:week-Leetcode
1502. Can Make Arithmetic Progression From Sequence
Given an array of numbers arr. A sequence of numbers is called an arithmetic progression if the difference between any two consecutive elements is the same.
Return true if the array can be rearranged to form an arithmetic progression, otherwise, return false.
Example 1:
Input: arr = [3,5,1]
Output: true
Explanation: We can reorder the elements as [1,3,5] or [5,3,1] with differences 2 and -2 respectively, between each consecutive elements.
Example 2:
Input: arr = [1,2,4]
Output: false
Explanation: There is no way to reorder the elements to obtain an arithmetic progression.
Constraints:
- 2 <= arr.length <= 1000
- -10^6 <= arr[i] <= 10^6
题解
/**
* @param {number[]} arr
* @return {boolean}
*/
const canMakeArithmeticProgression = function(arr) {
arr.sort((a,b)=>a-b);
console.log(arr)
let space=arr[1]-arr[0]
let flag=true
for(let i=2;i<arr.length;i++){
if(arr[i]-arr[i-1]!==space){
flag=false;
break;
}
}
return flag
};
1503. Last Moment Before All Ants Fall Out of a Plank
We have a wooden plank of the length n units. Some ants are walking on the plank, each ant moves with speed 1 unit per second. Some of the ants move to the left, the other move to the right.
When two ants moving in two different directions meet at some point, they change their directions and continue moving again. Assume changing directions doesn't take any additional time.
When an ant reaches one end of the plank at a time t, it falls out of the plank imediately.
Given an integer n and two integer arrays left and right, the positions of the ants moving to the left and the right. Return the moment when the last ant(s) fall out of the plank.
Example 1:
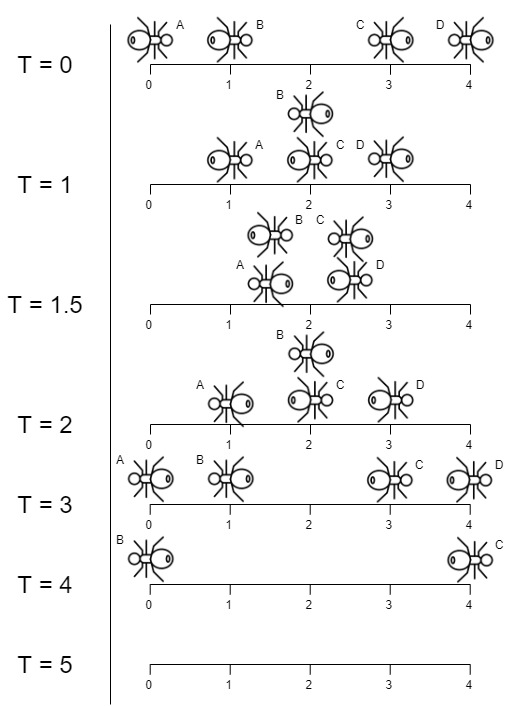
Input: n = 4, left = [4,3], right = [0,1]
Output: 4
Explanation: In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
Note that the last moment when an ant was on the plank is t = 4 second, after that it falls imediately out of the plank. (i.e. We can say that at t = 4.0000000001, there is no ants on the plank).
Example 2:

Input: n = 7, left = [], right = [0,1,2,3,4,5,6,7]
Output: 7
Explanation: All ants are going to the right, the ant at index 0 needs 7 seconds to fall.
Example 3:

Input: n = 7, left = [0,1,2,3,4,5,6,7], right = []
Output: 7
Explanation: All ants are going to the left, the ant at index 7 needs 7 seconds to fall.
Example 4:
Input: n = 9, left = [5], right = [4]
Output: 5
Explanation: At t = 1 second, both ants will be at the same intial position but with different direction.
Example 5:
Input: n = 6, left = [6], right = [0]
Output: 6
Constraints:
- 1 <= n <= 10^4
- 0 <= left.length <= n + 1
- 0 <= left[i] <= n
- 0 <= right.length <= n + 1
- 0 <= right[i] <= n
- 1 <= left.length + right.length <= n + 1
- All values of left and right are unique, and each value can appear only in one of the two arrays.
题解
/**
* left 向左爬,取最大值
* right 向右爬,取最小值
* @param {number} n
* @param {number[]} left
* @param {number[]} right
* @return {number}
*/
const getLastMoment = function(n, left, right) {
let maxSteps=0;
//遍历向左移动的🐜
for(let i=0;i<left.length;i++){
maxSteps=Math.max(left[i],maxSteps)
}
//遍历向右移动的🐜
for(let i=0;i<right.length;i++){
maxSteps=Math.max(n-right[i],maxSteps)
}
return maxSteps
};
1504. Count Submatrices With All Ones
Given a rows * columns matrix mat of ones and zeros, return how many submatrices have all ones.
Example 1:
Input: mat = [[1,0,1],
[1,1,0],
[1,1,0]]
Output: 13
Explanation:
There are 6 rectangles of side 1x1.
There are 2 rectangles of side 1x2.
There are 3 rectangles of side 2x1.
There is 1 rectangle of side 2x2.
There is 1 rectangle of side 3x1.
Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.
Example 2:
Input: mat = [[0,1,1,0],
[0,1,1,1],
[1,1,1,0]]
Output: 24
Explanation:
There are 8 rectangles of side 1x1.
There are 5 rectangles of side 1x2.
There are 2 rectangles of side 1x3.
There are 4 rectangles of side 2x1.
There are 2 rectangles of side 2x2.
There are 2 rectangles of side 3x1.
There is 1 rectangle of side 3x2.
Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.
Example 3:
Input: mat = [[1,1,1,1,1,1]]
Output: 21
Example 4:
Input: mat = [[1,0,1],[0,1,0],[1,0,1]]
Output: 5
Constraints:
- 1 <= rows <= 150
- 1 <= columns <= 150
- 0 <= mat[i][j] <= 1
题解
/**
* @param {number[][]} mat
* @return {number}
*/
const numSubmat = function(mat) {
let m = mat.length, n = mat[0].length;
let cnt=[]
for(let i=0;i<m;i++){
cnt[i]=[]
for(let j=0;j<n;j++){
cnt[i][j]=0
}
}
let total = 0;
for(let i = 0; i < m; i++) {
for(let j = 0; j < n; j++) {
if(mat[i][j] == 1) {
cnt[i][j] = (i > 0? cnt[i - 1][j]: 0) + 1;
total += cnt[i][j];
let min = cnt[i][j];
for(let k = j - 1; k >= 0; k--) {
if(cnt[i][k] > 0) {
min = Math.min(min, Math.min(cnt[i][k], cnt[i][j]));
total += min;
}else {
break;
}
}
}
}
}
return total;
};
1505. Minimum Possible Integer After at Most K Adjacent Swaps On Digits
Given a string num representing the digits of a very large integer and an integer k.
You are allowed to swap any two adjacent digits of the integer at most k times.
Return the minimum integer you can obtain also as a string.
Example 1:
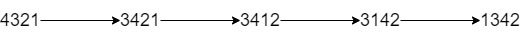
Input: num = "4321", k = 4
Output: "1342"
Explanation: The steps to obtain the minimum integer from 4321 with 4 adjacent swaps are shown.
Example 2:
Input: num = "100", k = 1
Output: "010"
Explanation: It's ok for the output to have leading zeros, but the input is guaranteed not to have any leading zeros.
Example 3:
Input: num = "36789", k = 1000
Output: "36789"
Explanation: We can keep the number without any swaps.
Example 4:
Input: num = "22", k = 22
Output: "22"
Example 5:
Input: num = "9438957234785635408", k = 23
Output: "0345989723478563548"
Constraints:
- 1 <= num.length <= 30000
- num contains digits only and doesn't have leading zeros.
- 1 <= k <= 10^9
题解
/**
* @param {string} num
* @param {number} k
* @return {string}
*/
const minInteger = function(num, k) {
let ca=num.split('');
helper(ca,0,k);
return ca.join('')
};
const helper = function(ca,I,k) {
if (k==0 || I==ca.length) return;
let min = ca[I], minIdx = I;
for (let i = I+1; i<Math.min(I+k+1, ca.length); i++)
if (ca[i]<min){
min=ca[i];
minIdx=i;
}
let temp = ca[minIdx];
for (let i = minIdx; i>I; i--) ca[i]=ca[i-1];
ca[I] = temp;
helper(ca, I+1, k-(minIdx-I));
}




