Weekly Contest 195
周赛地址(英):weekly contest 195
周赛地址(中):第 195 场周赛
仓库地址:week-Leetcode
1496. Path Crossing
Given a string path, where path[i] = 'N', 'S', 'E' or 'W', each representing moving one unit north, south, east, or west, respectively. You start at the origin (0, 0) on a 2D plane and walk on the path specified by path.
Return True if the path crosses itself at any point, that is, if at any time you are on a location you've previously visited. Return False otherwise.
Example 1:
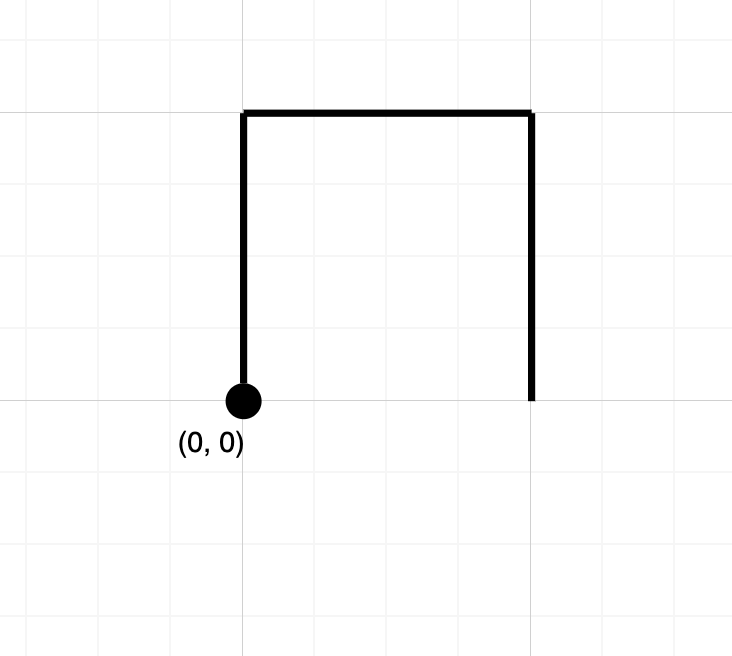
Input: path = "NES"
Output: false
Explanation: Notice that the path doesn't cross any point more than once.
Example 2:
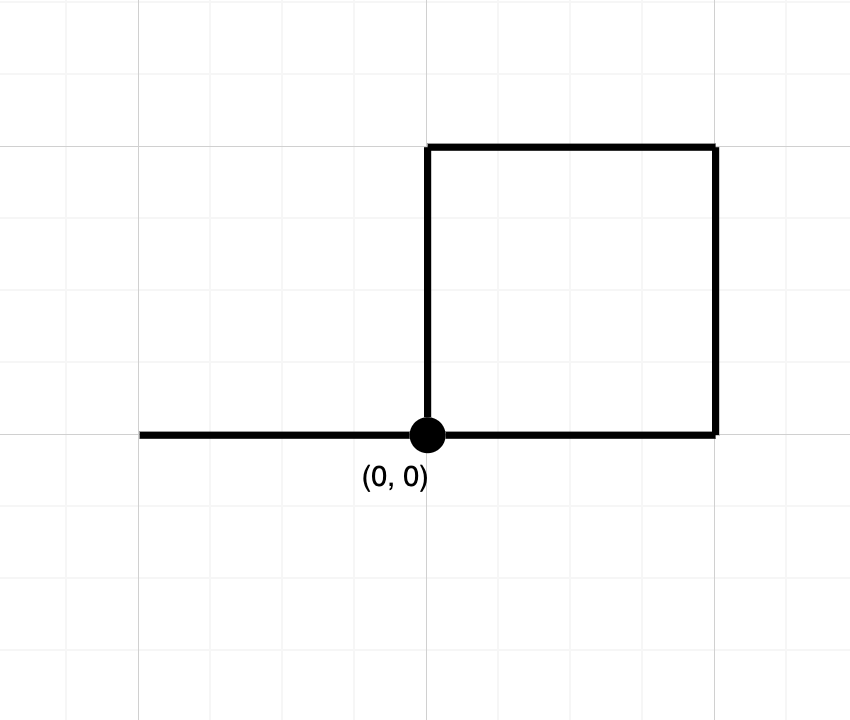
Input: path = "NESWW"
Output: true
Explanation: Notice that the path visits the origin twice.
Constraints:
- 1 <= path.length <= 10^4
- path will only consist of characters in
题解
/**
* @param {string} path
* @return {boolean}
*/
const isPathCrossing = function(path) {
let x=0,y=0;
let obj={'00':true}
for(let i=0;i<path.length;i++){
if(path[i]==='N') y++;
if(path[i]==='S') y--;
if(path[i]==='E') x++;
if(path[i]==='W') x--;
if(obj[x+''+y]) return true
obj[x+''+y]=true
}
return false
};
1497. Check If Array Pairs Are Divisible by k
Given an array of integers arr of even length n and an integer k.
We want to divide the array into exactly n / 2 pairs such that the sum of each pair is divisible by k.
Return True If you can find a way to do that or False otherwise.
Example 1:
Input: arr = [1,2,3,4,5,10,6,7,8,9], k = 5
Output: true
Explanation: Pairs are (1,9),(2,8),(3,7),(4,6) and (5,10).
Example 2:
Input: arr = [1,2,3,4,5,6], k = 7
Output: true
Explanation: Pairs are (1,6),(2,5) and(3,4).
Example 3:
Input: arr = [1,2,3,4,5,6], k = 10
Output: false
Explanation: You can try all possible pairs to see that there is no way to divide arr into 3 pairs each with sum divisible by 10.
Example 4:
Input: arr = [-10,10], k = 2
Output: true
Example 5:
Input: arr = [-1,1,-2,2,-3,3,-4,4], k = 3
Output: true
Constraints:
- arr.length == n
- 1 <= n <= 10^5
- n is even.
- -10^9 <= arr[i] <= 10^9
- 1 <= k <= 10^5
题解
/**
* @param {number[]} arr
* @param {number} k
* @return {boolean}
*/
const canArrange = function(arr, k) {
let sum=0;
for(let item of arr){
sum+=item
}
return sum%k===0
};
1498. Number of Subsequences That Satisfy the Given Sum Condition
Given an array of integers nums and an integer target.
Return the number of non-empty subsequences of nums such that the sum of the minimum and maximum element on it is less or equal than target.
Since the answer may be too large, return it modulo 10^9 + 7.
Example 1:
Input: nums = [3,5,6,7], target = 9
Output: 4
Explanation: There are 4 subsequences that satisfy the condition.
[3] -> Min value + max value <= target (3 + 3 <= 9)
[3,5] -> (3 + 5 <= 9)
[3,5,6] -> (3 + 6 <= 9)
[3,6] -> (3 + 6 <= 9)
Example 2:
Input: nums = [3,3,6,8], target = 10
Output: 6
Explanation: There are 6 subsequences that satisfy the condition. (nums can have repeated numbers).
[3] , [3] , [3,3], [3,6] , [3,6] , [3,3,6]
Example 3:
Input: nums = [2,3,3,4,6,7], target = 12
Output: 61
Explanation: There are 63 non-empty subsequences, two of them don't satisfy the condition ([6,7], [7]).
Number of valid subsequences (63 - 2 = 61).
Example 4:
Input: nums = [5,2,4,1,7,6,8], target = 16
Output: 127
Explanation: All non-empty subset satisfy the condition (2^7 - 1) = 127
Constraints:
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^6
- 1 <= target <= 10^6
题解
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
const numSubseq = function(nums, target) {
const mod = 1000000007;
const powersOf2 = [];
let powerOf2 = 1;
for (let i = 0; i < nums.length; i++) {
powersOf2.push(powerOf2);
powerOf2 = powerOf2 * 2 % mod;
}
nums.sort((a,b) => a - b);
let count = 0;
let j = nums.length - 1;
for (let i = 0; i < nums.length && nums[i] + nums[i] <= target; i++) {
while (j && nums[j] + nums[i] > target) j--;
count = (count + powersOf2[j - i]) % mod;
}
return count;
};
1499. Max Value of Equation
Given an array points containing the coordinates of points on a 2D plane, sorted by the x-values, where points[i] = [xi, yi] such that xi < xj for all 1 <= i < j <= points.length. You are also given an integer k.
Find the maximum value of the equation yi + yj + |xi - xj| where |xi - xj| <= k and 1 <= i < j <= points.length. It is guaranteed that there exists at least one pair of points that satisfy the constraint |xi - xj| <= k.
Example 1:
Input: points = [[1,3],[2,0],[5,10],[6,-10]], k = 1
Output: 4
Explanation: The first two points satisfy the condition |xi - xj| <= 1 and if we calculate the equation we get 3 + 0 + |1 - 2| = 4. Third and fourth points also satisfy the condition and give a value of 10 + -10 + |5 - 6| = 1.
No other pairs satisfy the condition, so we return the max of 4 and 1.
Example 2:
Input: points = [[0,0],[3,0],[9,2]], k = 3
Output: 3
Explanation: Only the first two points have an absolute difference of 3 or less in the x-values, and give the value of 0 + 0 + |0 - 3| = 3.
Constraints:
- 2 <= points.length <= 10^5
- points[i].length == 2
- -10^8 <= points[i][0], points[i][1] <= 10^8
- 0 <= k <= 2 * 10^8
- points[i][0] < points[j][0] for all 1 <= i < j <= points.length
- xi form a strictly increasing sequence.
题解
/**
* @param {number[][]} points
* @param {number} k
* @return {number}
*/
var findMaxValueOfEquation = function(points, k) {
const monoQ = new MaxMonoqueue();
let j = 0;
let max = -Infinity;
for (const [x, y] of points) {
while (!monoQ.isEmpty() && x - points[j][0] > k) {
monoQ.dequeue();
j++;
}
max = Math.max(max, x + y + monoQ.max());
monoQ.enqueue(y - x);
}
return max;
};
class MaxMonoqueue {
constructor() {
this.head = new Node();
this.tail = this.head;
}
enqueue(value) {
let count = 1
while (!this.isEmpty() && value > this.tail.value) {
count += this.tail.count;
const { prev: node } = this.tail;
this.tail.prev = null;
node.next = null;
this.tail = node;
}
this.tail.next = new Node(value, count);
this.tail.next.prev = this.tail;
this.tail = this.tail.next;
}
dequeue() {
if (this.isEmpty()) return
const { next: node } = this.head;
node.count--;
if (!node.count) {
this.head = this.head.next;
this.head.setToHead()
}
}
max() {
if (this.isEmpty()) return -Infinity;
return this.head.next.value;
}
isEmpty() {
return this.head === this.tail;
}
}
class Node {
constructor(value = -Infinity, count = -Infinity) {
this.value = value;
this.count = count;
this.next = this.prev = null;
}
setToHead() {
this.value = -Infinity;
this.count = -Infinity;
this.prev = null;
}
}




