算法——二叉树的遍历 前序 中序 后序 广度优先 深度优先 (转)
二叉树的遍历
1、先序遍历
先序遍历的顺序是:先根节点,再左节点,再右节点,即根节点->左节点->右节点。
如:
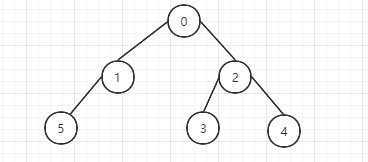
先序遍历的顺序为:0,1,5,2,3,4
2、中序遍历
中序遍历的顺序为,先左节点,再根节点,再右节点,即左节点->根节点->右节点。
还是以下面的二叉树为例:
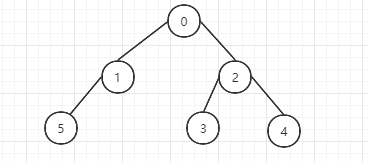
中序遍历的顺序为:5,1,0,3,2,4
3、后序遍历
后序遍历的顺序是:先左节点,再右节点,再根节点,即左节点->右节点->根节点。
还是以上面的二叉树为例:
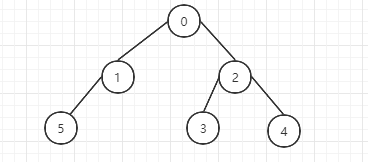
后序遍历的顺序为:5,1,3,4,2,0
4、广度优先遍历
广度优先遍历的顺序是:从根节点向下,从左到右遍历,下面还是拿上面的二叉树为例:
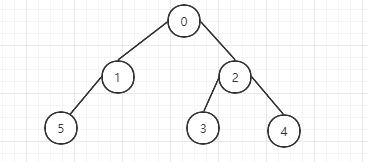
广度优先遍历顺序为:0,1,2,5,3,4
/** * 二叉树的广度优先遍历 */ public List<Integer> bfs(TreeNode root) { Queue<TreeNode> queue = new LinkedList<TreeNode>(); List<Integer> list=new LinkedList<Integer>(); if(root==null) return list; queue.add(root); while (!queue.isEmpty()){ TreeNode t=queue.remove(); if(t.left!=null) queue.add(t.left); if(t.right!=null) queue.add(t.right); list.add(t.val); } return list;
5、深度优先遍历
深度优先遍历的顺序为:先从根节点一直往下直到叶子节点进行遍历,然后叶子节点回到其父节点的右节点进行遍历。
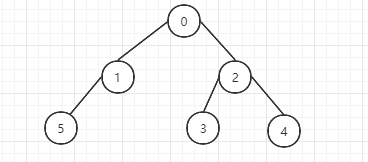
深度优先遍历顺序:0,1,5,2,3,4
/** * 二叉树的深度优先遍历 * @param root * @return */ public List<Integer> dfs(TreeNode root){ Stack<TreeNode> stack=new Stack<TreeNode>(); List<Integer> list=new LinkedList<Integer>(); if(root==null) return list; //压入根节点 stack.push(root); //然后就循环取出和压入节点,直到栈为空,结束循环 while (!stack.isEmpty()){ TreeNode t=stack.pop(); if(t.right!=null) stack.push(t.right); if(t.left!=null) stack.push(t.left); list.add(t.val); } return list; }
public void solution(TreeNode root) { List<Integer> list=new LinkedList<Integer>(); depthTraversal(list,root); } private void dfs(List<Integer> list,TreeNode tn) { if (tn!=null) { list.add(tn); //每次先添加左节点,直到没有子节点点,返回上一级 dfs(tn.left); dfs(tn.right); }






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律