吴恩达机器学习笔记 —— 2 单变量线性回归
第一章讲述了基本的机器学习的概念以及分类,这里从单变量的线性回归入手,吴恩达讲解了机器学习中的几个重要因素,如模型、损失函数、优化方法等
更多内容参考 机器学习&深度学习
首先以房价预测入手:
| 房子的面积 | 每平米的房价 |
|---|---|
| 2104 | 460 |
| 1416 | 232 |
| 1534 | 315 |
| 852 | 178 |
其中:
- m 为 样本的数量
- x 是样本的特征
- y 是预测的值
- 就是一条样本数据
- 是第i条样本
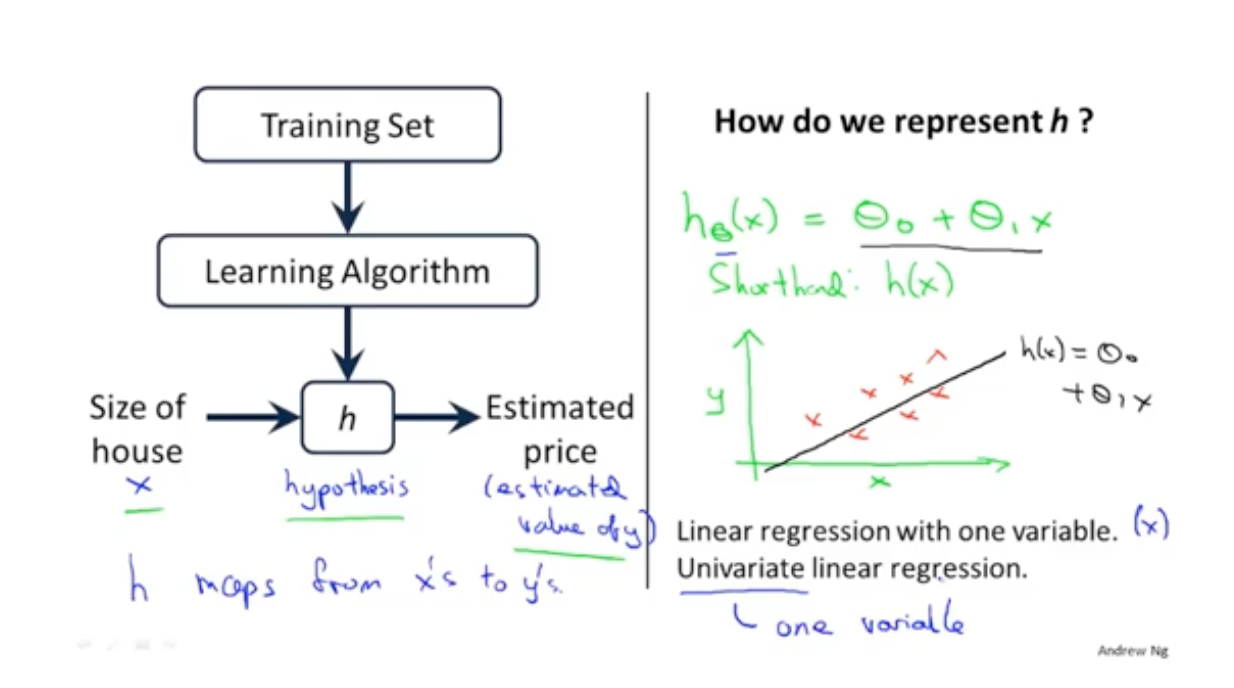
机器学习的过程就是通过上面的例子学习一个模型,当再次有数据x进来的时候,能给出对应的y值
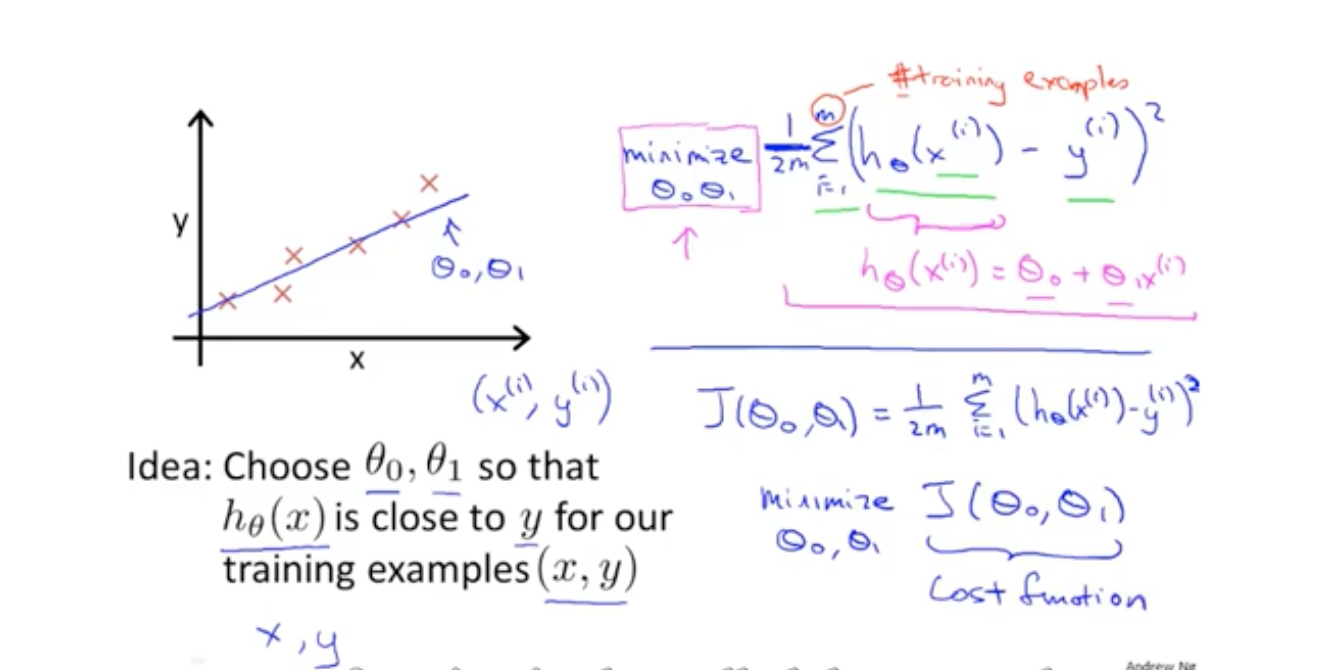
代价函数就是真实的值与我们预测的值之间的偏差,由于偏差有可能正,有可能负,因此使用均方差来表示。

不同的参数对应的损失值是不一样的,最终机器学习的目的就是寻找这个损失之最低的方法。
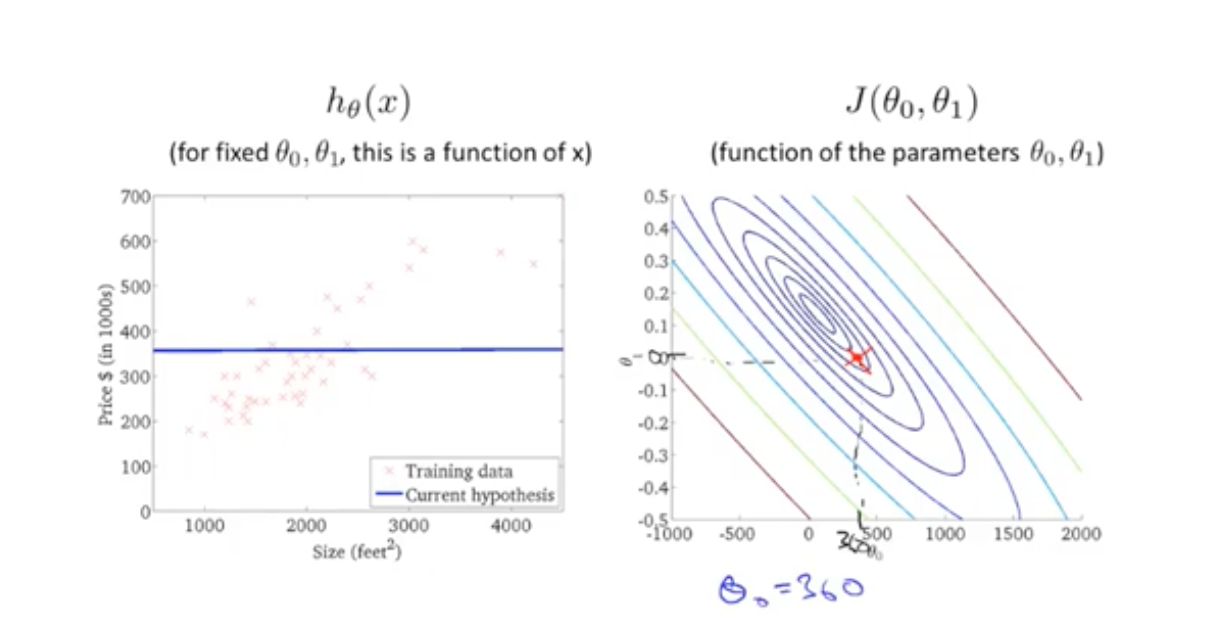
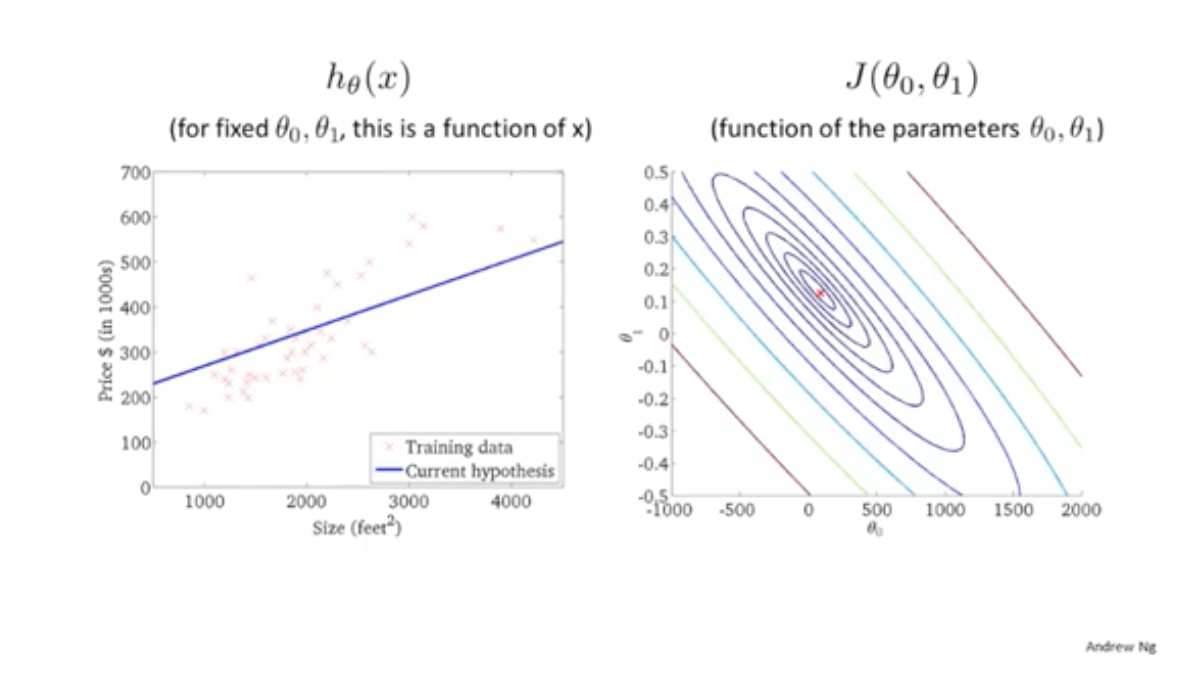
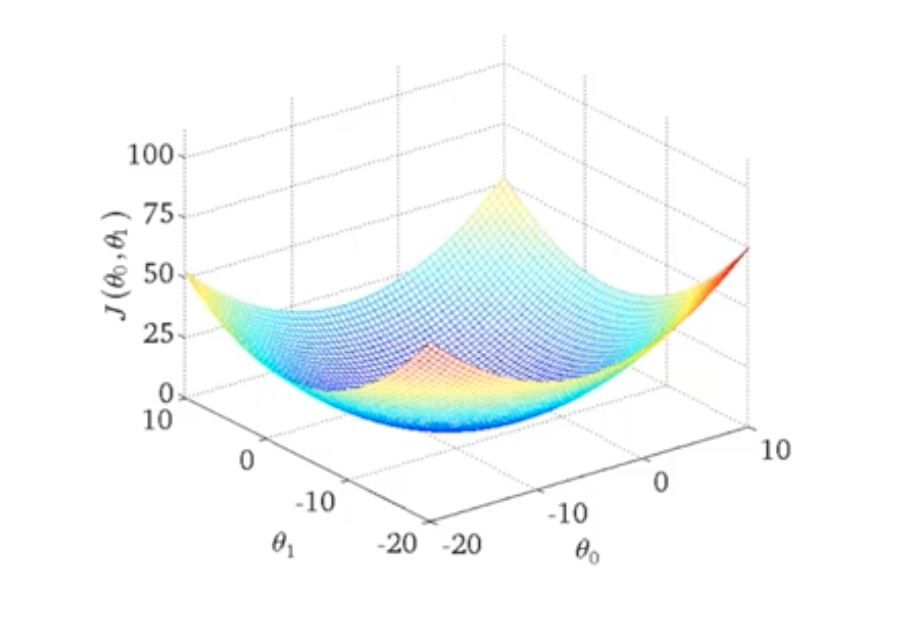
在二维特征下,可以看成一个关于损失函数的等高线图。同一个线圈,损失函数的值是相同的。在越来越靠近中心点时,可以看到预测的直线越来越贴近样本值。证明在等高线最中心的位置(最低点),损失值是最小的。
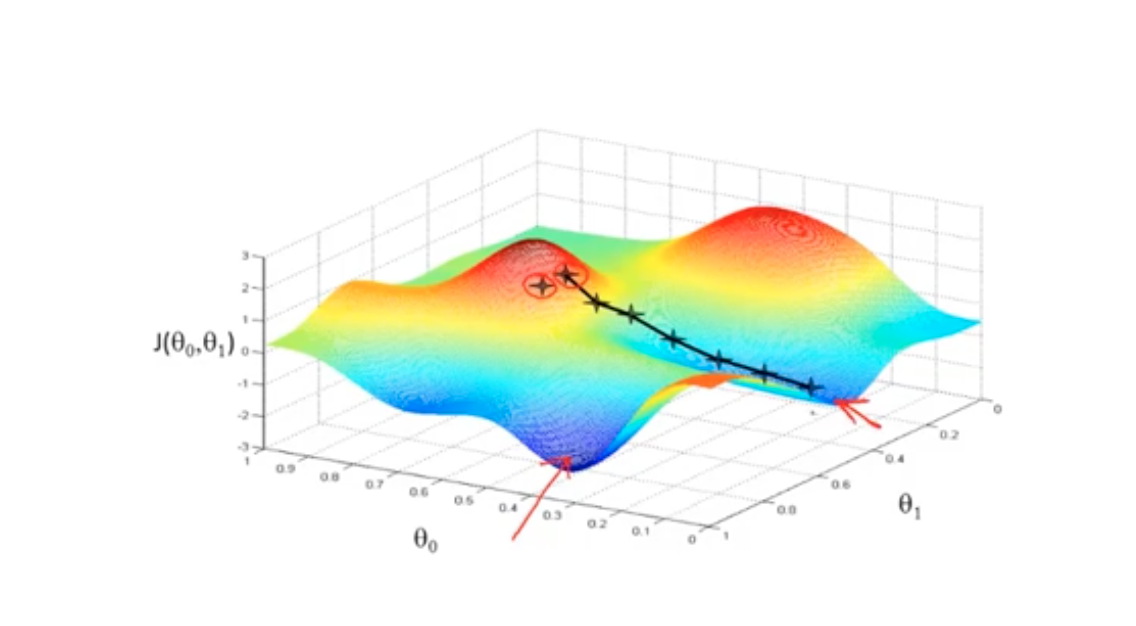
梯度下降可能找到是一个局部最优解,而不是全局最优解。

- 参数随着每次迭代而改变
- α是学习率,可以控制每次步长的变化
- 每次改变的长度是基于偏导求解的
- 在修改参数时,应该统一计算修改的值,再统一进行调整
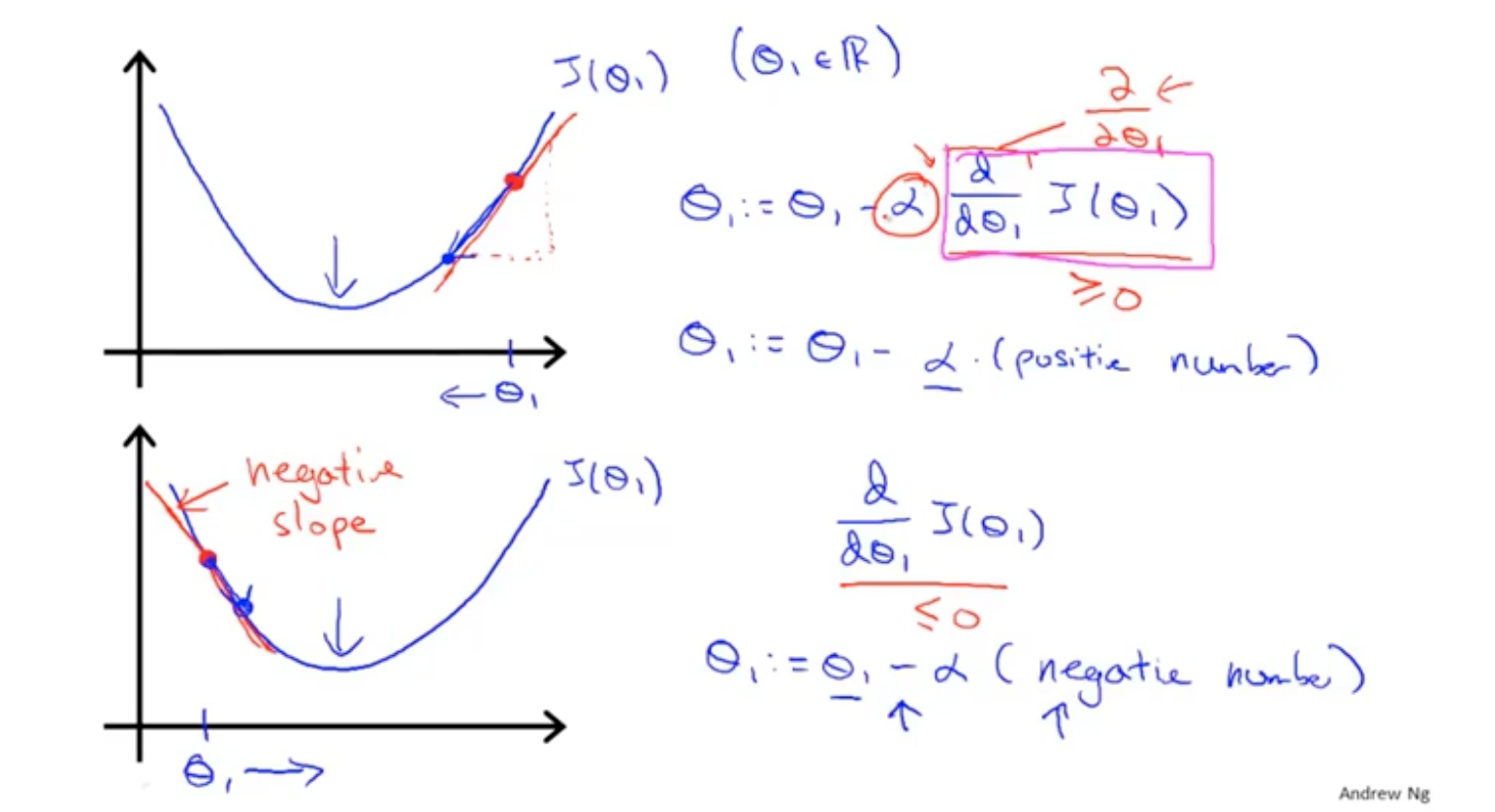
无论在最低点的哪一侧,公式都能保证θ是朝着最低点的位置在变化。
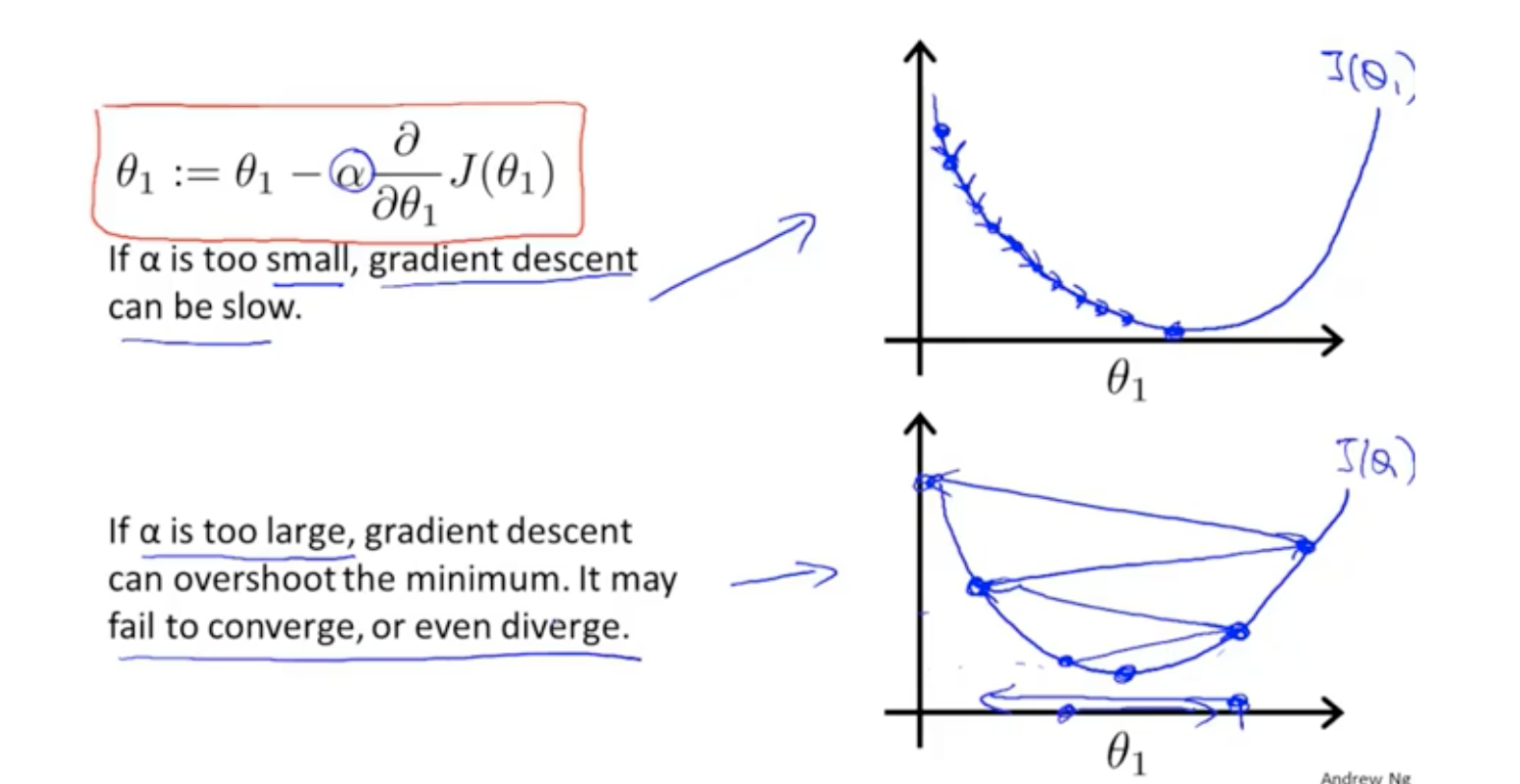
学习率的大小决定了能否快速找到最优解。
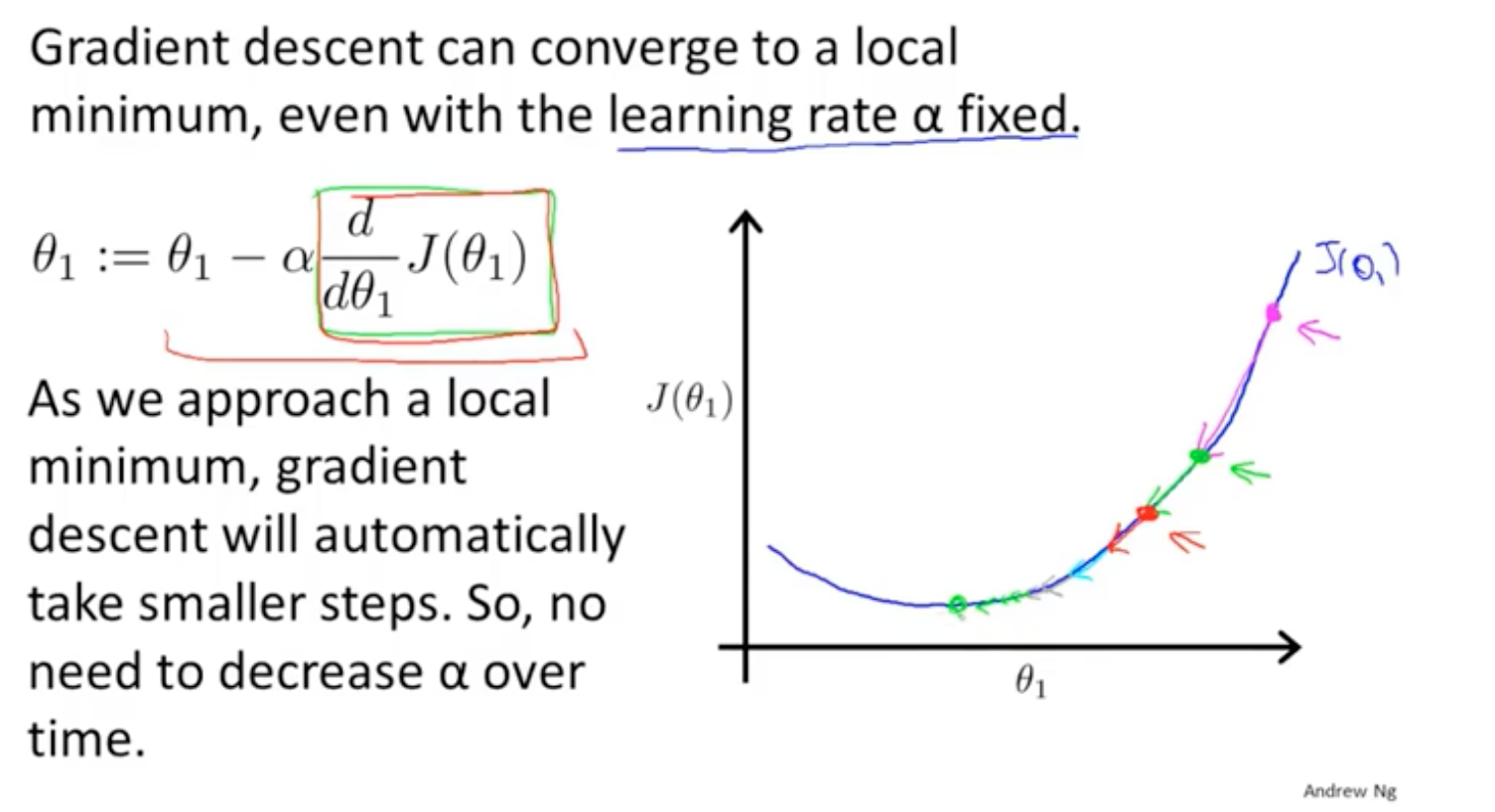
随机梯度下降在靠近最优解的时候,步长将会变得越来越小。

线性回归中,梯度下降是上面这样的。

针对优化的方法,有batch梯度下降、随机梯度下降、mini-batch梯度下降等等
batch梯度下降
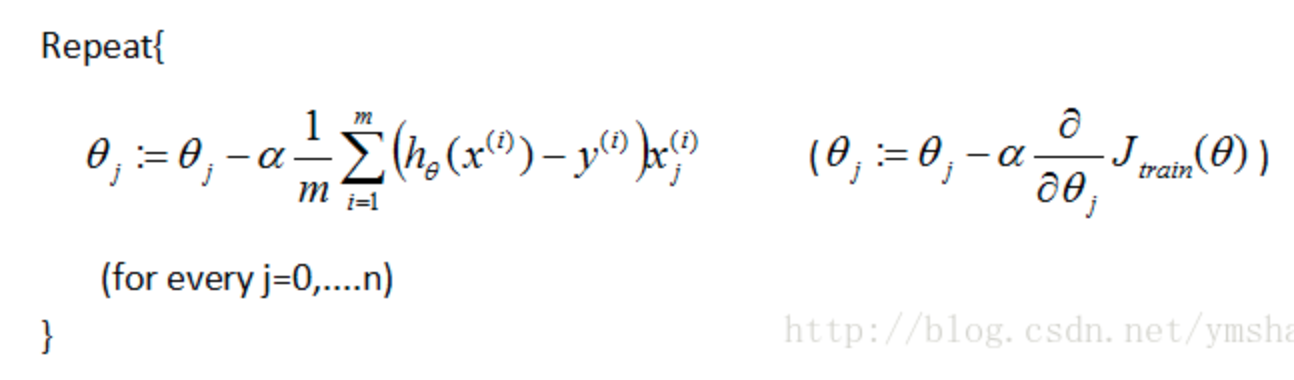
随机梯度下降
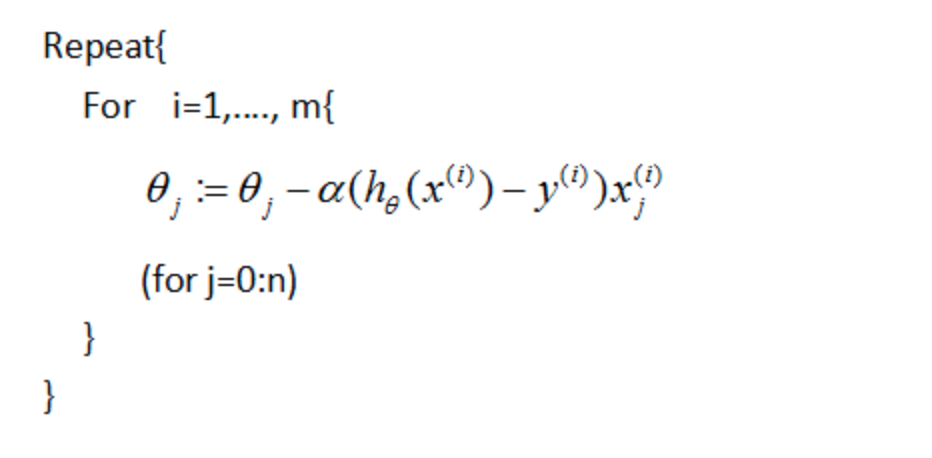
mini-batch梯度下降
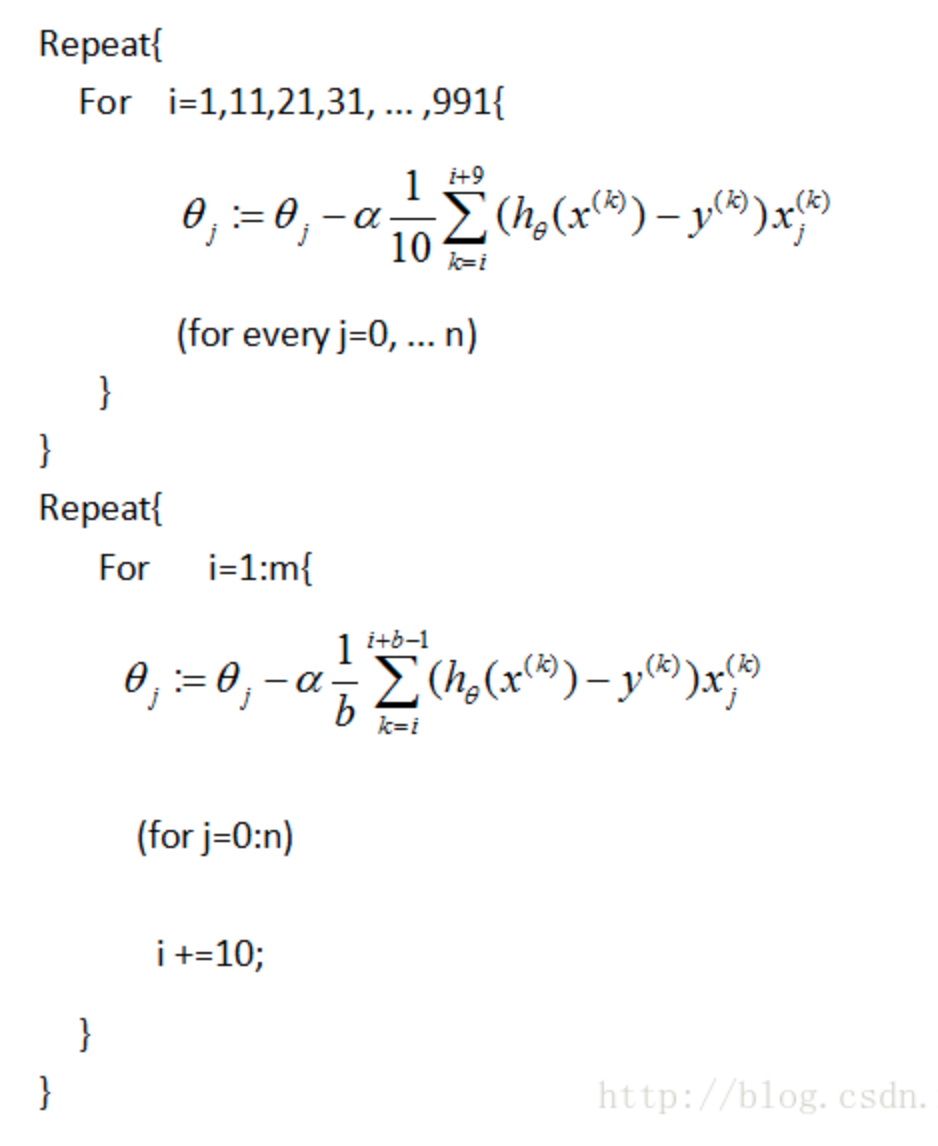




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 分享 3 个 .NET 开源的文件压缩处理库,助力快速实现文件压缩解压功能!
· Ollama——大语言模型本地部署的极速利器
· DeepSeek如何颠覆传统软件测试?测试工程师会被淘汰吗?
2016-07-10 Oracle使用小记