SM2数据加密(公钥私钥模式)
import cn.hutool.core.util.CharsetUtil; import cn.hutool.core.util.StrUtil; import cn.hutool.crypto.SecureUtil; import cn.hutool.crypto.SmUtil; import cn.hutool.crypto.asymmetric.KeyType; import cn.hutool.crypto.asymmetric.SM2; import lombok.extern.slf4j.Slf4j; import org.apache.commons.codec.binary.Base64; import org.springframework.stereotype.Component; import org.springframework.util.StringUtils; import java.io.UnsupportedEncodingException; import java.security.KeyPair; @Slf4j @Component("SM2Util") public class SM2Util { private static SM2 sm2; /**私钥*/ final private static String privateKey = "调用下面的getSM2Key生成";//自己调用下面的getSM2Key生成 /**公钥*/ final private static String publicKey = "调用下面的getSM2Key生成";//自己调用下面的getSM2Key生成 private static synchronized SM2 getSm2() { if (sm2 == null) { // Environment environment = SpringBeanUtil.getApplicationContext().getEnvironment(); // String privateKey = environment.getProperty("encrypt.sm2.privateKey"); // String publicKey = environment.getProperty("encrypt.sm2.publicKey"); sm2 = SmUtil.sm2(Base64.decodeBase64(privateKey), Base64.decodeBase64(publicKey)); } return sm2; } /** * 公钥加密 * * @param cipherTxt * @return */ public static String encrypt(String cipherTxt) { if (!StringUtils.hasText(cipherTxt)) { return cipherTxt; } String encryptStr = getSm2().encryptBcd(cipherTxt, KeyType.PublicKey); return encryptStr; } /** * 私钥解密 * * @param plainTxt * @return */ public static String decrypt(String plainTxt) { if (!StringUtils.hasText(plainTxt)) { return plainTxt; } String decryptStr = StrUtil.utf8Str(getSm2().decryptFromBcd(plainTxt, KeyType.PrivateKey)); return decryptStr; } /** * 生成一对 C1C2C3 格式的SM2密钥 * * @return 处理结果 */ public static void getSM2Key() { KeyPair pair = SecureUtil.generateKeyPair("SM2"); byte[] privateKey = pair.getPrivate().getEncoded(); byte[] publicKey = pair.getPublic().getEncoded(); try { System.out.println("私钥" + new String(Base64.encodeBase64(privateKey), CharsetUtil.UTF_8)); System.out.println("公钥" + new String(Base64.encodeBase64(publicKey), CharsetUtil.UTF_8)); } catch (UnsupportedEncodingException e) { log.error(e.getMessage()); } } public static void main(String[] args) { // getSM2Key(); String name = "张三"; String mi = encrypt(name); System.out.println(mi); System.out.println(decrypt(mi)); } }
引入的Maven依赖(目前看好像可以不引)
<dependency>
<groupId>cn.hutool</groupId>
<artifactId>hutool-all</artifactId>
</dependency>
<!-- SM2加密 -->
<dependency>
<groupId>org.bouncycastle</groupId>
<artifactId>bcprov-jdk15on</artifactId>
<version>1.64</version>
</dependency>
复杂的知识:
国密系列算法简介
其中SM1、SM4、SM7、祖冲之密码(ZUC)是对称算法;SM2、SM9是非对称算法;SM3是哈希算法。目前,这些算法已广泛应用于各个领域中,期待有一天会有采用国密算法的区块链应用出现。
1、SM1对称密码
SM1 算法是分组密码算法,分组长度为128位,密钥长度都为 128 比特,算法安全保密强度及相关软硬件实现性能与 AES 相当,算法不公开,仅以IP核的形式存在于芯片中。
采用该算法已经研制了系列芯片、智能IC卡、智能密码钥匙、加密卡、加密机等安全产品,广泛应用于电子政务、电子商务及国民经济的各个应用领域(包括国家政务通、警务通等重要领域)。
2、SM2椭圆曲线公钥密码算法
SM2算法就是ECC椭圆曲线密码机制,但在签名、密钥交换方面不同于ECDSA、ECDH等国际标准,而是采取了更为安全的机制。另外,SM2推荐了一条256位的曲线作为标准曲线。
SM2标准包括总则,数字签名算法,密钥交换协议,公钥加密算法四个部分,并在每个部分的附录详细说明了实现的相关细节及示例。
SM2算法主要考虑素域Fp和F2m上的椭圆曲线,分别介绍了这两类域的表示,运算,以及域上的椭圆曲线的点的表示,运算和多倍点计算算法。然后介绍了编程语言中的数据转换,包括整数和字节串,字节串和比特串,域元素和比特串,域元素和整数,点和字节串之间的数据转换规则。详细说明了有限域上椭圆曲线的参数生成以及验证,椭圆曲线的参数包括有限域的选取,椭圆曲线方程参数,椭圆曲线群基点的选取等,并给出了选取的标准以便于验证。最后给椭圆曲线上密钥对的生成以及公钥的验证,用户的密钥对为(s,sP),其中s为用户的私钥,sP为用户的公钥,由于离散对数问题从sP难以得到s,并针对素域和二元扩域给出了密钥对生成细节和验证方式。总则中的知识也适用于SM9算法。在总则的基础上给出了数字签名算法(包括数字签名生成算法和验证算法),密钥交换协议以及公钥加密算法(包括加密算法和解密算法),并在每个部分给出了算法描述,算法流程和相关示例。
数字签名算法,密钥交换协议以及公钥加密算法都使用了国家密管理局批准的SM3密码杂凑算法和随机数发生器。数字签名算法,密钥交换协议以及公钥加密算法根据总则来选取有限域和椭圆曲线,并生成密钥对。
3、SM3杂凑算法
SM3密码杂凑(哈希、散列)算法给出了杂凑函数算法的计算方法和计算步骤,并给出了运算示例。此算法适用于商用密码应用中的数字签名和验证,消息认证码的生成与验证以及随机数的生成,可满足多种密码应用的安全需求。在SM2,SM9标准中使用。
此算法对输入长度小于2的64次方的比特消息,经过填充和迭代压缩,生成长度为256比特的杂凑值,其中使用了异或,模,模加,移位,与,或,非运算,由填充,迭代过程,消息扩展和压缩函数所构成。具体算法及运算示例见SM3标准。
4、SM4对称算法
此算法是一个分组算法,用于无线局域网产品。该算法的分组长度为128比特,密钥长度为128比特。加密算法与密钥扩展算法都采用32轮非线性迭代结构。解密算法与加密算法的结构相同,只是轮密钥的使用顺序相反,解密轮密钥是加密轮密钥的逆序。
此算法采用非线性迭代结构,每次迭代由一个轮函数给出,其中轮函数由一个非线性变换和线性变换复合而成,非线性变换由S盒所给出。其中rki为轮密钥,合成置换T组成轮函数。轮密钥的产生与上图流程类似,由加密密钥作为输入生成,轮函数中的线性变换不同,还有些参数的区别。SM4算法的具体描述和示例见SM4标准。
5、SM7对称密码
SM7算法,是一种分组密码算法,分组长度为128比特,密钥长度为128比特。SM7适用于非接触式IC卡,应用包括身份识别类应用(门禁卡、工作证、参赛证),票务类应用(大型赛事门票、展会门票),支付与通卡类应用(积分消费卡、校园一卡通、企业一卡通等)。
6、SM9标识密码算法
为了降低公开密钥系统中密钥和证书管理的复杂性,以色列科学家、RSA算法发明人之一Adi Shamir在1984年提出了标识密码(Identity-Based Cryptography)的理念。标识密码将用户的标识(如邮件地址、手机号码、QQ号码等)作为公钥,省略了交换数字证书和公钥过程,使得安全系统变得易于部署和管理,非常适合端对端离线安全通讯、云端数据加密、基于属性加密、基于策略加密的各种场合。2008年标识密码算法正式获得国家密码管理局颁发的商密算法型号:SM9(商密九号算法),为我国标识密码技术的应用奠定了坚实的基础。
SM9算法不需要申请数字证书,适用于互联网应用的各种新兴应用的安全保障。如基于云技术的密码服务、电子邮件安全、智能终端保护、物联网安全、云存储安全等等。这些安全应用可采用手机号码或邮件地址作为公钥,实现数据加密、身份认证、通话加密、通道加密等安全应用,并具有使用方便,易于部署的特点,从而开启了普及密码算法的大门。
7、ZUC祖冲之算法
祖冲之序列密码算法是中国自主研究的流密码算法,是运用于移动通信4G网络中的国际标准密码算法,该算法包括祖冲之算法(ZUC)、加密算法(128-EEA3)和完整性算法(128-EIA3)三个部分。目前已有对ZUC算法的优化实现,有专门针对128-EEA3和128-EIA3的硬件实现与优化。
四、其它参考
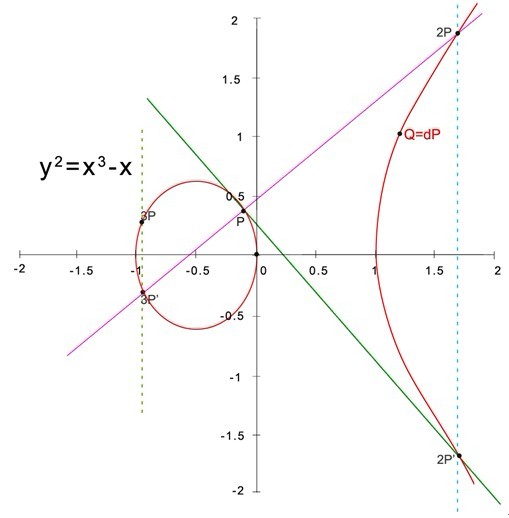
sm2算法,相关网址
http://www.oscca.gov.cn/sca/xxgk/2010-12/17/1002386/files/b791a9f908bb4803875ab6aeeb7b4e03.pdf
https://github.com/teclan/teclan-utils/blob/master/src/main/java/teclan/utils/security/SM2Utils.java
关于bouncycastle下国密SM2 API的使用 - jeffreyluo - 博客园
sm2: SM2加密解密java示例 - Gitee.com
https://github.com/guanzhi/GmSSL/
国密算法SM2证书制作_Mr.Kim.Wu 的日记-CSDN博客_国密证书
通过openssl生成sm2的公私钥的方法_dong_beijing的博客-CSDN博客_openssl 生成sm2
https://cloud.tencent.com/developer/article/1057477
用gmssl制作国密SM2证书_hknaruto的专栏-CSDN博客_gmssl sm2证书
sm2证书生成(单证书)_csj50的专栏-CSDN博客_生成sm2证书
openssl - 数字证书的编程解析 - huhu0013 - 博客园


 浙公网安备 33010602011771号
浙公网安备 33010602011771号