南大2021高级机器学习期末复习

目录

• 十、降维和度量学习
  • 10.1、k-近邻学习
    • 10.1.1、懒惰学习
    • 10.1.2、KNN错误率
  • 10.2、低维嵌入
    • 10.2.1、维数灾难
    • 10.2.2、多维数缩放方法MDS
  • 10.3、PCA
    • 10.3.1、最近重构性:样本点到这个超平面的距离都足够近
    • 10.3.2、最大可分性:样本点在这个超平面上的投影能尽可能分开
  • 10.3.3、求解
  • 10.4、流形学习
    • 10.4.1、核化PAC
    • 10.4.2、ISOMAP
    • 10.4.3、LLE
  • 10.5、度量学习
    • 10.5.1、马氏距离
• 十一、特征选择和稀疏学习
  • 11.1、子集搜索
  • 11.2、子集评价
  • 11.3、常见的特征选择方法
    • 11.3.1、Filter：过滤法
      • 11.3.1.1、Relief方法
      • 11.3.1.2、其扩展变体Relief-F能处理多分类问题
    • 11.3.2、包裹式
      • 11.3.2.1、LVW
    • 11.3.3、嵌入式
      • 11.3.3.1、岭回归 (ridge regression) [Tikhonov and Arsenin, 1977]
      • 11.3.3.2、将L2范数替换为L1范数，则有LASSO [Tibshirani, 1996]
  • 11.4、使用范数正则化易获得稀疏解
  • 11.5、稀疏表示
  • 11.6、矩阵补全
• 十二、半监督学习
  • 12.1、高斯混合模型（Gaussian Mixture Model）通常简称GMM
  • 12.2、TSVM
  • 12.3、图半监督学习
  • 12.4、基于分歧
  • 12.5、半监督聚类
• 十三、概率图模型:基本概念和方法
  • 13.1、隐马尔可夫模型(动态贝叶斯网)
  • 13.2、马尔可夫随机场
  • 13.3、条件随机场
  • 13.4、学习与推断
    • 13.4.1、精确推断
    • 13.4.2、信念传播
    • 13.4.3、近似推断
      • 13.4.3.1、MCMC采样
      • 13.4.3.2、MH算法
    • 13.4.4、变分推断
  • 13.5、话题模型
• 十四、强化学习简介
  • 14.1、MDP

十、降维和度量学习

10.1、k-近邻学习

10.1.1、懒惰学习

不关心学到什么，只一字不差的存储内容

10.1.2、KNN错误率

最近邻分离器的错误率：设样本x，最近邻z，错误率为1-(x和z同类)

X=z时，求得最近邻分离器的泛化错误率<=2*最优贝叶斯分类器的泛化错误率。

\[\begin{aligned} P(e r r) &=1-\sum_{c \in \mathcal{Y}} P(c \mid \boldsymbol{x}) P(c \mid \boldsymbol{z}) \\ & \simeq 1-\sum_{c \in \mathcal{Y}} P^{2}(c \mid \boldsymbol{x}) \\ & \leqslant 1-P^{2}\left(c^{*} \mid \boldsymbol{x}\right) \\ &=\left(1+P\left(c^{*} \mid \boldsymbol{x}\right)\right)\left(1-P\left(c^{*} \mid \boldsymbol{x}\right)\right) \\ & \leqslant 2 \times\left(1-P\left(c^{*} \mid \boldsymbol{x}\right)\right) \end{aligned} \]

最近邻分类器虽简单，但它的泛化错误率不超过贝叶斯最优分类器的错误率的两倍!

10.2、低维嵌入

10.2.1、维数灾难

在高维情形下出现的数据样本稀疏、 距离计算困难等问题， 是所有机器学习方法共同面临的严重障碍， 被称为维数灾难。

10.2.2、多维数缩放方法MDS

MDS (Multiple Dimensional Scaling) 旨在寻找一个低维子空间，

样本在此子空间内的距离和样本原有距离尽量保持不变

---

输入:距离矩阵 \(\mathbf{D} \in \mathbb{R}^{m \times m}\), 其元素 \(d i s t_{i j}\) 为样本 \(x_{i}\) 到 \(x_{j}\) 的距离; 低维空间维数d' :

过程：

1: 计算\({dist}_{i .}^{2}\),\({dist}_{. j}^{2}\),\({dist}_{. .}^{2}\)

\[\begin{aligned} \text { dist }_{i .}^{2} &=\frac{1}{m} \sum_{j=1}^{m} \operatorname{dist}_{i j}^{2} \\ \text { dist }_{\cdot j}^{2} &=\frac{1}{m} \sum_{i=1}^{m} \operatorname{dist}_{i j}^{2} \\ \text { dist }_{. .}^{2} &=\frac{1}{m^{2}} \sum_{i=1}^{m} \sum_{j=1}^{m} d i s t_{i j}^{2} \end{aligned} \]

2: 由此即可通过降维前后保持不变的距离矩阵 D 求取内积矩阵 B.

\[b_{i j}=-\frac{1}{2}\left(d i s t_{i j}^{2}-d i s t_{i .}^{2}-d i s t_{\cdot j}^{2}+\right. dist.. \left.^{2}\right) \]

3: 对矩阵 B 做特征值分解;
\(B = V{\Lambda}V^T\)

其中 \({\Lambda} = diag(λ_1,λ_2， ...，{\lambda}_d)\)为特征值构成的对角矩阵，

4: 取 \(\tilde{\Lambda}\) 为 d' 个最大特征值所构成的对角矩阵，\(\tilde{V}\)为相应的特征向量矩阵.

输出:矩阵\(\tilde{\mathbf{V}} \tilde{\mathbf{\Lambda}}^{1 / 2} \in \mathbb{R}^{m \times d^{\prime}}\)，每行是一个样本的低维坐标

---

10.3、PCA

https://blog.csdn.net/u010910642/article/details/51442939

10.3.1、最近重构性:样本点到这个超平面的距离都足够近

考虑整个训练集，原样本点\(x_i\)与基于投影重构的样本点\(\hat{x_i}\)之间的距离为

\[\begin{aligned} \sum_{i=1}^{m}\left\|\sum_{j=1}^{d^{\prime}} z_{i j} \boldsymbol{w}_{j}-\boldsymbol{x}_{i}\right\|_{2}^{2} &=\sum_{i=1}^{m} \boldsymbol{z}_{i}^{\mathrm{T}} \boldsymbol{z}_{i}-2 \sum_{i=1}^{m} \boldsymbol{z}_{i}^{\mathrm{T}} \mathbf{W}^{\mathrm{T}} \boldsymbol{x}_{i}+\mathrm{const((\sum{x}_{i}^{{T}} {x}_{i})} \\ & \propto-\operatorname{tr}\left(\mathbf{W}^{\mathrm{T}}\left(\sum_{i=1}^{m} \boldsymbol{x}_{i} \boldsymbol{x}_{i}^{\mathrm{T}}\right) \mathbf{W}\right) \end{aligned} \]

\(\propto\)代表是正比

\(\boldsymbol{w}_{j}\) 是正交基 \(\sum_{i} \boldsymbol{x}_{i} \boldsymbol{x}_{i}^{\mathrm{T}}\) 是协方差矩阵，于是由最近重构性，有：

\[\begin{array}{cl} \min _{\mathbf{W}} & -\operatorname{tr}\left(\mathbf{W}^{\mathrm{T}} \mathbf{X} \mathbf{X}^{\mathrm{T}} \mathbf{W}\right) \\ \text { s.t. } & \mathbf{W}^{\mathrm{T}} \mathbf{W}=\mathbf{I} \end{array} \]

10.3.2、最大可分性:样本点在这个超平面上的投影能尽可能分开

样本点\(x_i\)在新空间上的投影为\(W^Tx_i\)
若所有样本点能近可能分开，则应该使投影后样本的方差最大，即\(\sum_ix_i^TWW^Tx_i\)
由\(x_i^TWW^Tx_i\)=\(tr(W^Tx_ix^T_iW)\)
可知优化目标函数为

\[\begin{array}{cl} \max _{\mathbf{W}} & \operatorname{tr}\left(\mathbf{W}^{\mathrm{T}} \mathbf{X} \mathbf{X}^{\mathrm{T}} \mathbf{W}\right) \\ \text { s.t. } & \mathbf{W}^{\mathrm{T}} \mathbf{W}=\mathbf{I} \end{array} \]

10.3.3、求解

\[\begin{array}{cl} \max _{\mathbf{W}} & \operatorname{tr}\left(\mathbf{W}^{\mathrm{T}} \mathbf{X} \mathbf{X}^{\mathrm{T}} \mathbf{W}\right) \\ \text { s.t. } & \mathbf{W}^{\mathrm{T}} \mathbf{W}=\mathbf{I} \end{array} \]

使用拉格朗日乘子法可得

\(XX^TW = {\lambda}W\)

只需对协方差矩阵 \(XX^T\) 进行特征值分解，并将求得的特征值排序\(:{\lambda}_1,{\lambda}_ 2 ··· {\lambda}_d\) ，再取前 d’ 个特征值对应的特征向量构成 \(W = (w_1, w_2, . . . , w_{d'} )\)，这就是主成分分析的解。

10.4、流形学习

线性降维方法假设从高维空间到低维空间的函数映射是线性的,然而在许多现实任务中，可能需要非线性映射才能找到恰当的低维嵌入

10.4.1、核化PAC

核化PCA:加了一个核函数

假定 \(z_{i}\) 是由原始属性空间中样本点通过映射 \(\phi\) 产生, 即 \(_{\mathbf{z}_{i}}=\phi\left(\boldsymbol{x}_{i}\right), i=1,2, \ldots, m\)
于是有

\[\begin{array}{l} \left(\sum_{i=1}^{m} \phi\left(\mathbf{x}_{i}\right) \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\right) \mathbf{W}=\lambda \mathbf{W}, \\ \mathbf{W}=\sum_{i=1}^{m} \phi\left(\boldsymbol{x}_{i}\right) \boldsymbol{\alpha}_{i} \end{array} \]

令 \(\kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}} \phi\left(\boldsymbol{x}_{j}\right)\) 可得 \(\mathbf{K A}=\lambda \mathbf{A}, \mathbf{A}=\left(\boldsymbol{\alpha}_{1} ; \boldsymbol{\alpha}_{\mathbf{2}} ; \ldots ; \boldsymbol{\alpha}_{\mathbf{m}}\right)\)
于是

\[\begin{aligned} z_{j} &=\boldsymbol{w}_{j}^{\mathrm{T}} \phi(\boldsymbol{x})=\sum_{i=1}^{m} \alpha_{i}^{j} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}} \phi(\boldsymbol{x}) \\ &=\sum_{i=1}^{m} \alpha_{i}^{j} \kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right) \end{aligned} \]

10.4.2、ISOMAP

• 构造近邻图
• 基于最短路径算法近似任意两点之间的测地线(geodesic)距离
• 基于距离矩阵通过MDS获得低维嵌入

10.4.3、LLE

• 为每个样本构造近邻集合\(Q_i\)

• 为每个样本计算基于Qi的线性重构系数

  \[\begin{aligned} \min _{\mathbf{w}_{1}, \mathbf{w}_{2}, \ldots, \mathbf{w}_{m}} & \sum_{i=1}^{m}\left\|\boldsymbol{x}_{i}-\sum_{j \in Q_{i}} w_{i j} \boldsymbol{x}_{j}\right\|_{2}^{2} \\ \text { s.t. } & \sum_{j \in Q_{i}} w_{i j}=1, \\ \end{aligned} \]

• 在低维空间中保持\(w_{ij}\) 不变，求解下式

  \[\\ \min _{\mathbf{z}_{1}, \mathbf{z}_{2}, \ldots, \mathbf{z}_{m}} \sum_{i=1}^{m}\left\|\boldsymbol{z}_{i}-\sum_{j \in Q_{i}} w_{i j} \boldsymbol{z}_{j}\right\|_{2}^{2} \]

10.5、度量学习

10.5.1、马氏距离

马氏距离就是特征空间通过矩阵L做完线性变换后的欧式距离。当L为单位阵时，马氏距离就等于欧式距离。

\[\operatorname{dist}_{\operatorname{mah}}^{2}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\left(\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right)^{\mathrm{T}} \mathbf{M}\left(\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right)=\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right\|_{\mathrm{M}}^{2} \]

其中 M 是一个半正定对称矩阵，亦称“度量矩阵”，距离度量学习就是要对 M 进行学习

十一、特征选择和稀疏学习

11.1、子集搜索

用贪心策略选择包含重要信息的特征子集

前向搜索:逐渐增加相关特征
后向搜索:从完整的特征集合开始，逐渐减少特征
双向搜索:每一轮逐渐增加相关特征，同时减少无关特征

11.2、子集评价

\[\operatorname{Gain}(A)=\operatorname{Ent}(D)-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right) \]

其中信息熵定义为：

\[\operatorname{Ent}(D)=-\sum_{i=1}^{|\mathcal{Y}|} p_{k} \log _{2} p_{k} \]

信息增益 Gain(A) 越大，意味着特征子集 A 包含的有助于分类的信息越多.于 是，对每个候选特征子集，我们可基于训练数据集 D 来计算其信息增益，以此作为评价准则.

11.3、常见的特征选择方法

11.3.1、Filter：过滤法

先对特征集进行特征选择，然后再训练学习器

特点：特征选择过程与后续学习器无关，直接“过滤”特征

方法：对各个特征进行评分，设定阈值或者待选择阈值的个数，来选择特征。

11.3.1.1、Relief方法

针对二分类问题。

1、给定训练集\({(x_1,y_1),(x_2,y_2)...(x_m,y_m,)}\)。

2、对每个示例，先在\(x_{i}\),的同类样本中寻找其最近邻\(x_{i,nh}\)，称为“猜中近邻”(near-hit) 。

3、再从\(x_i\);的异类样本中寻找最近邻\(x_{i,nm}\)，称为“猜错近邻”(near-miss)， 然后相关统计量。

4、在对应属性j的分量为
\(\delta_{j}=\sum_{i}-\operatorname{diff}\left(x_{i}^{j}-x_{i, n h}^{j}\right)^{2}+\operatorname{diff}\left(x_{i}^{j}-x_{i, n m}^{j}\right)^{2}\)

5、其中\(x_{a}^j\),表示样本\(x_{a}\)在属性j上的取值。注意x。已经归一化到[0,1]区间。

6、从上面的式子可以看出，若\(x_i\)与其猜中近邻\(x_{i,nh}\)在属性j上的距离小于与其猜错近邻\(x_{i,nm}\)的距离，则说明属性j对区分同类与异类样本是有益的，反之，则说明是无意义的。

11.3.1.2、其扩展变体Relief-F能处理多分类问题

\(\delta^{j}=\sum_{i}-\operatorname{diff}\left(x_{i}^{j}, x_{i, n h}^{j}\right)^{2}+\sum_{l \neq k}\left(p_{l} \times \operatorname{diff}\left(x_{i}^{j}, x_{i, l, n m}^{j}\right)^{2}\right)\)

\(p_l\)为第l类样本在数据集D中所占的比例

11.3.2、包裹式

直接把最终将要使用的学习器的性能作为特征子集的评价准则，选择的是“量身定做”的特征子集。

特点：多个特征联合评价，对子集进行模型训练和评价。

11.3.2.1、LVW

LVW（拉斯维加斯方法）：随机产生特征子集，使用交叉验证来估计学习器的误差，当在新特征子集上表现的误差更小，或者误差相当但包含的特征更少，就将新特征子集保留下来。

• 在循环的每一轮随机产生一个特征子集

• 在随机产生的特征子集上通过交叉验证推断当前特征子集的误差

• 进行多次循环，在多个随机产生的特征子集中选择误差最小的特征子集作为最终解*

• 若有运行时间限制，则该算法有可能给不出解

蒙特卡洛：在规定时间给出不符合要求的解。

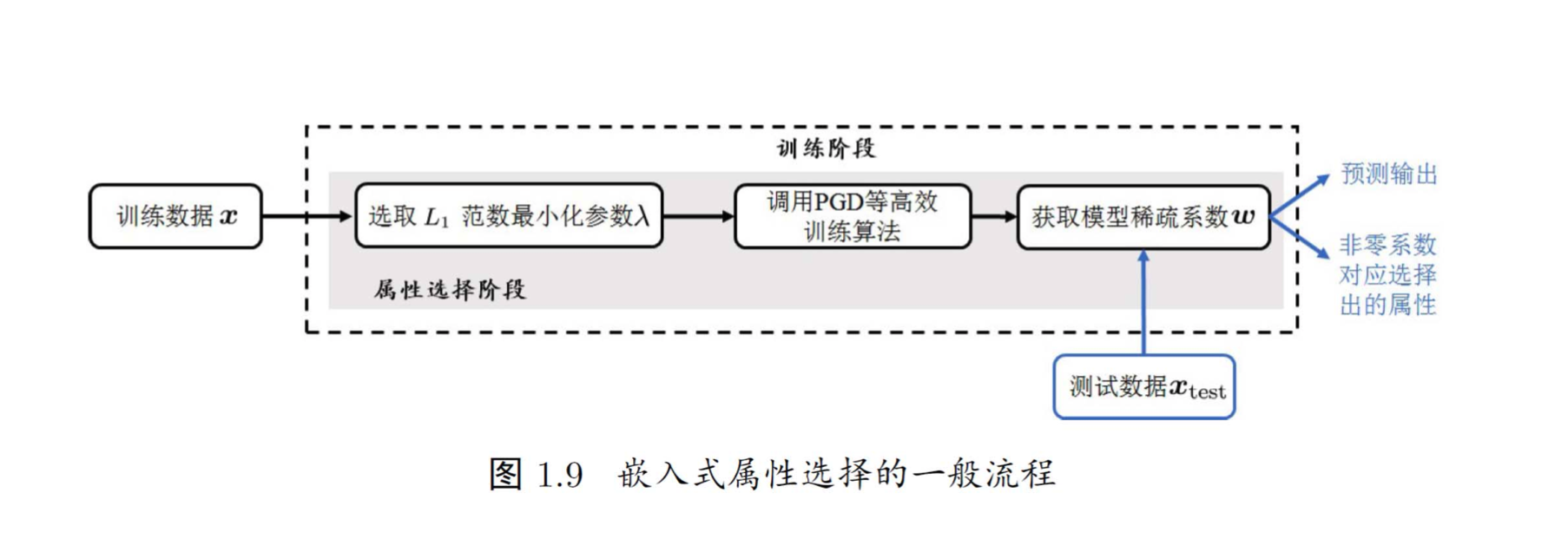
11.3.3、嵌入式

特点：嵌入法将两者融为一体，在同一个优化过程中完成，在学习训练的过程中，自动进行了特征选择。

方法：先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。

为了防止过拟合，会引入正则化项

考虑最简单的线性回归模型，以平方误差为损失函数，并引入\(L_2\)范数正则化项防止过拟合，则有

11.3.3.1、岭回归 (ridge regression) [Tikhonov and Arsenin, 1977]

\(\min _{\boldsymbol{w}} \sum_{i=1}^{m}\left(y_{i}-\boldsymbol{w}^{\top} \boldsymbol{x}_{i}\right)^{2}+\lambda\|\boldsymbol{w}\|_{2}^{2}\)

11.3.3.2、将L2范数替换为L1范数，则有LASSO [Tibshirani, 1996]

易获得稀疏解，是一种嵌入式特 征选择方法

\(\min _{\boldsymbol{w}} \sum_{i=1}^{m}\left(y_{i}-\boldsymbol{w}^{\top} \boldsymbol{x}_{i}\right)^{2}+\lambda\|\boldsymbol{w}\|_{1}\)

11.4、使用范数正则化易获得稀疏解

L1正则化的解具有稀疏性，可用于特征选择。

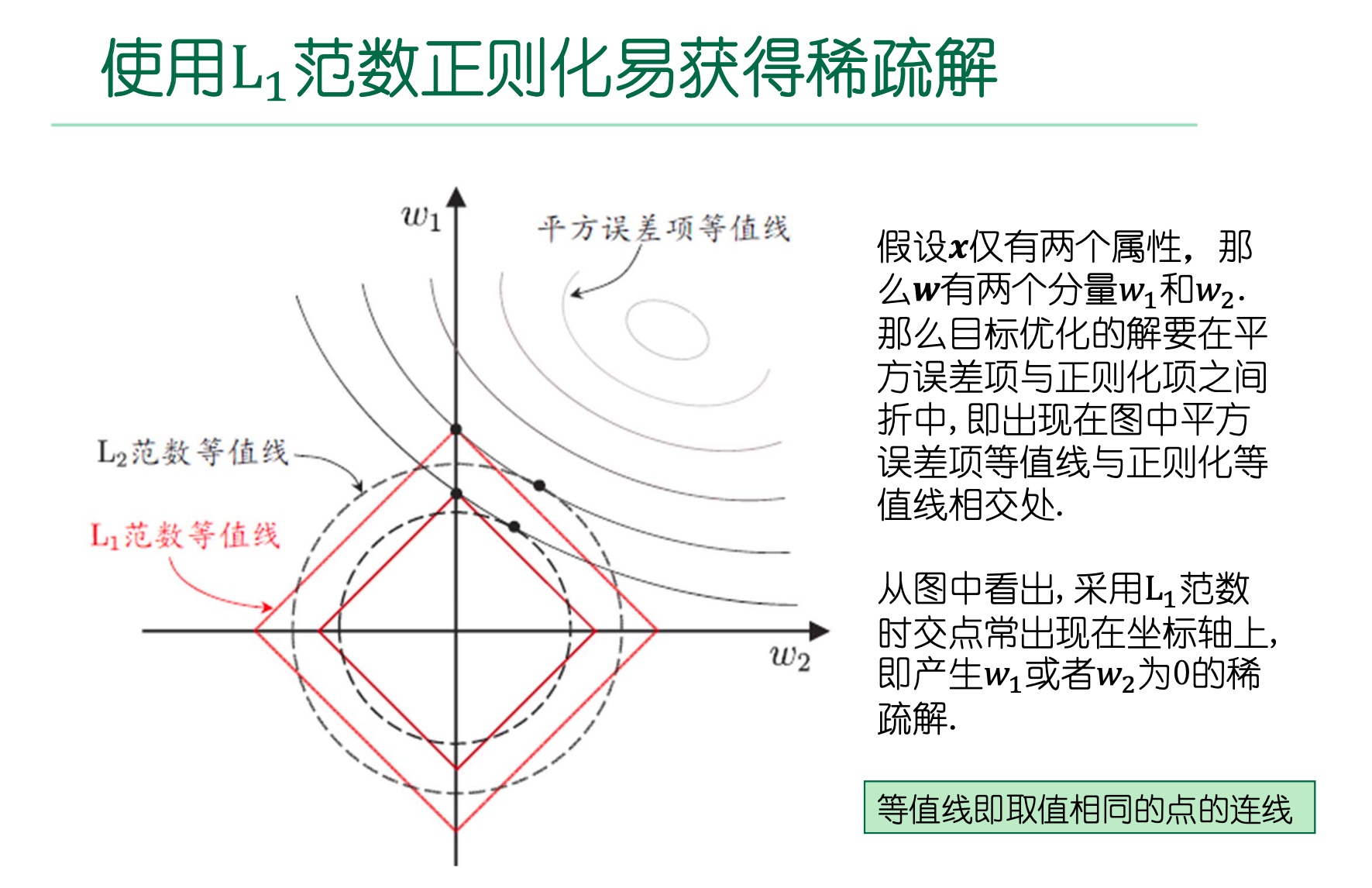
L1正则化方法：近端梯度下降。

L2正则化的解都比较小，抗扰动能力强。

从贝叶斯的角度，L2相当于给θ一个先验分布为高斯分布

11.5、稀疏表示

稀疏表示：特征—>矩阵，矩阵->稀疏矩阵

文本数据线性可分l 存储高效

普通稠密表达的样本找到合适的字典，将样本转化为稀疏表示，这一过程称为字典学习。

压缩感知：利用部分数据恢复全部数据。

𝐴具有“限定等距性”时，可以近乎完美地恢复𝒔

11.6、矩阵补全

NP难问题. 将rank(𝐗)转化为其凸包“核范数”（nuclear norm）

凸优化问题，通过半正定规划求解（SDP，Semi-Definite

十二、半监督学习

12.1、高斯混合模型（Gaussian Mixture Model）通常简称GMM

1、通过观察采样的概率值和模型概率值的接近程度，来判断一个模型是否拟合良好。

2、然后我们通过调整模型以让新模型更适配采样的概率值。反复迭代这个过程很多次，直到两个概率值非常接近时，我们停止更新并完成模型训练。

3、我们要将这个过程用算法来实现，所使用的方法是模型生成的数据来决定似然值，即通过模型来计算数据的期望值。

4、通过更新参数μ和σ来让期望值最大化。

5、这个过程可以不断迭代直到两次迭代中生成的参数变化非常小为止。

12.2、TSVM

https://blog.csdn.net/u011826404/article/details/74358913

监督学习中的SVM试图找到一个划分超平面，使得两侧支持向量之间的间隔最大，即“最大划分间隔”思想。对于半监督学习，S3VM则考虑超平面需穿过数据低密度的区域。TSVM是半监督支持向量机中的最著名代表，其核心思想是：尝试为未标记样本找到合适的标记指派，使得超平面划分后的间隔最大化。TSVM采用局部搜索的策略来进行迭代求解，即首先使用有标记样本集训练出一个初始SVM，接着使用该学习器对未标记样本进行打标，这样所有样本都有了标记，并基于这些有标记的样本重新训练SVM，之后再寻找易出错样本不断调整。整个算法流程如下所示：

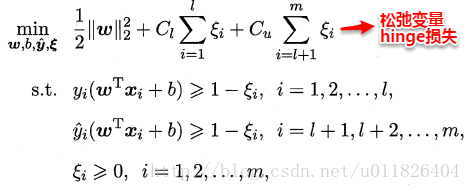
类别不平衡问题：

\(C_u^+=\frac{u_-}{u_+}C_u^-\)

开销巨大

12.3、图半监督学习

12.4、基于分歧

两个“充分”(sufficient)且“条件独立”视图。

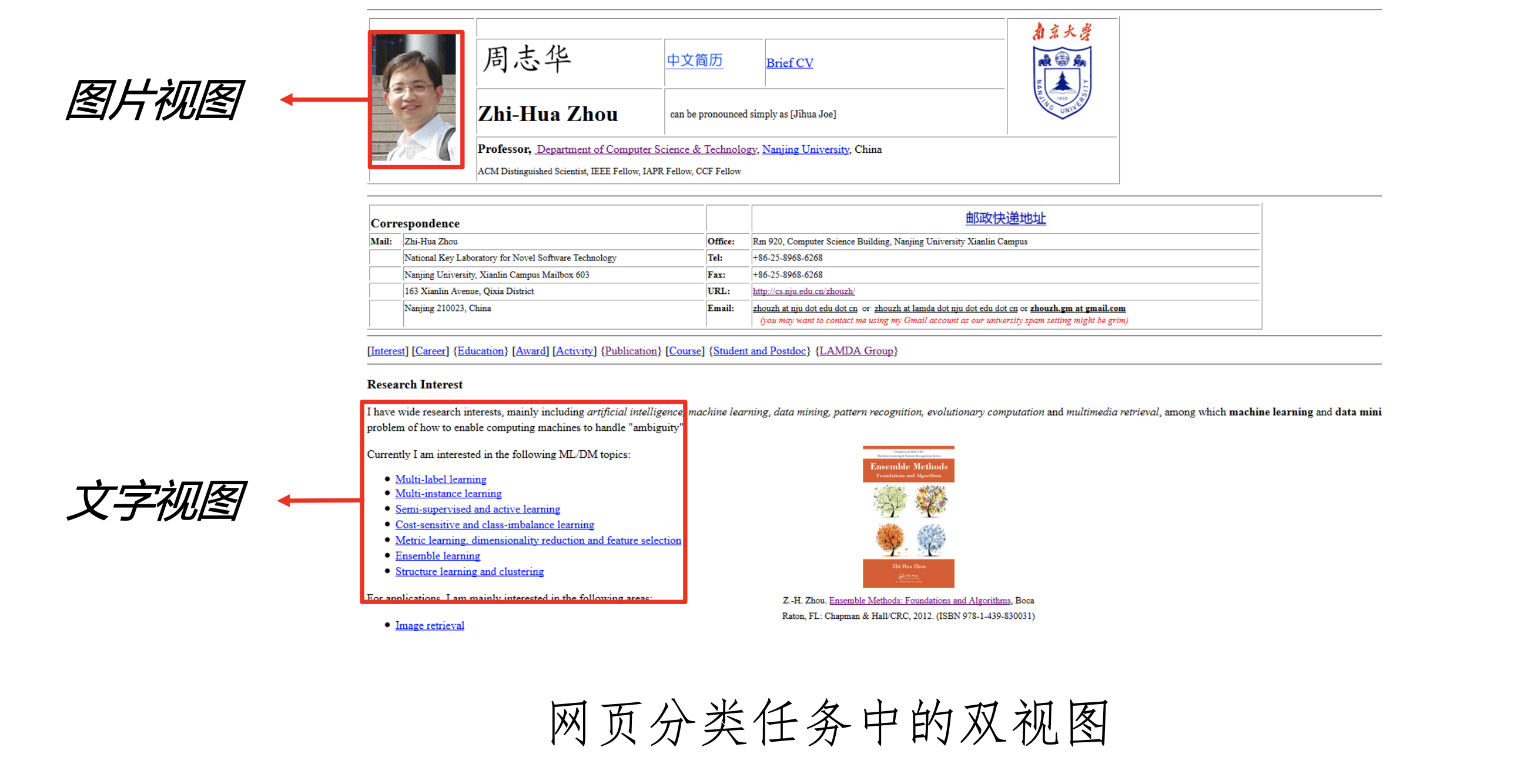
两个learner分别给无标记数据生成一个伪标签喂给另一个learner，进行训练。

仅需弱学习器之间具有显著的分歧(或差异), 即可通过相互提供伪标记样本的方式来提高泛化性能。

特点：

• 只需采用合适的基学习器，学习方法简单有效、理论基础相对坚实、适用范围较为广泛。

• 需能生成具有显著分歧、性能尚可的多个学习器,

• 但当有标记样本很少、尤其是数据不具有多视图时, 要做到这一点并不容易。

12.5、半监督聚类

基于无监督，有标记样本提供额外的监督信息。

1. 勿连和必连：约束k均值。选择最近簇时出错不满足要求则选择次近簇。约束k均值算法。

   1. 该算法是k均值算法的扩展,它在聚类过程中要确保“必连 ”关系集合与“勿连”关系集合中的约束得以满足，否则将返回错误提示。

2. 类标：第二种监督信息是少量有标记样本。即假设少量有标记样本属于k个聚类簇。

   1. 约束种子k均值。作为聚类种子初始化，更新簇时不计算，计算簇中心计算，

十三、概率图模型:基本概念和方法

13.1、隐马尔可夫模型(动态贝叶斯网)

13.2、马尔可夫随机场

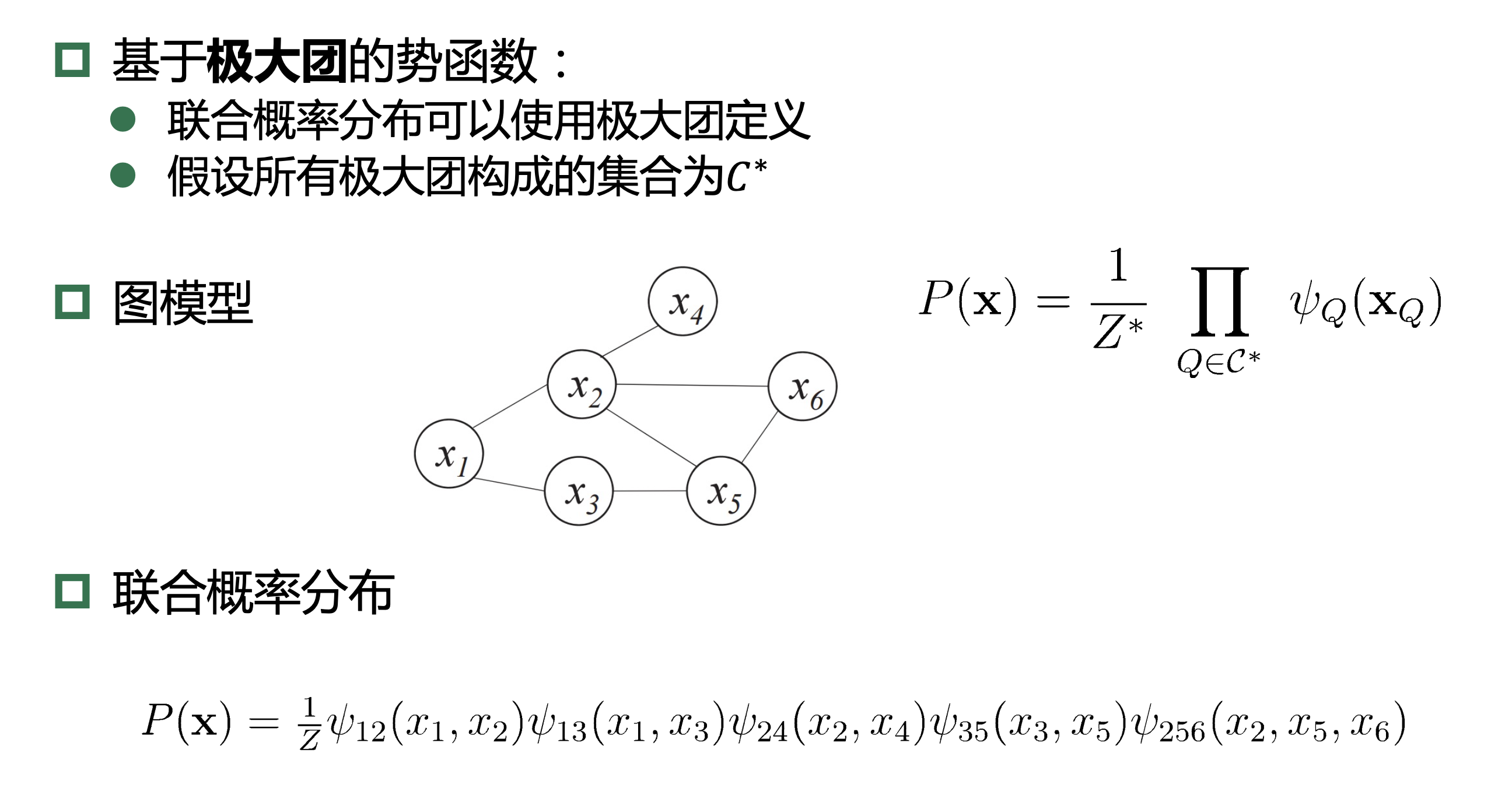
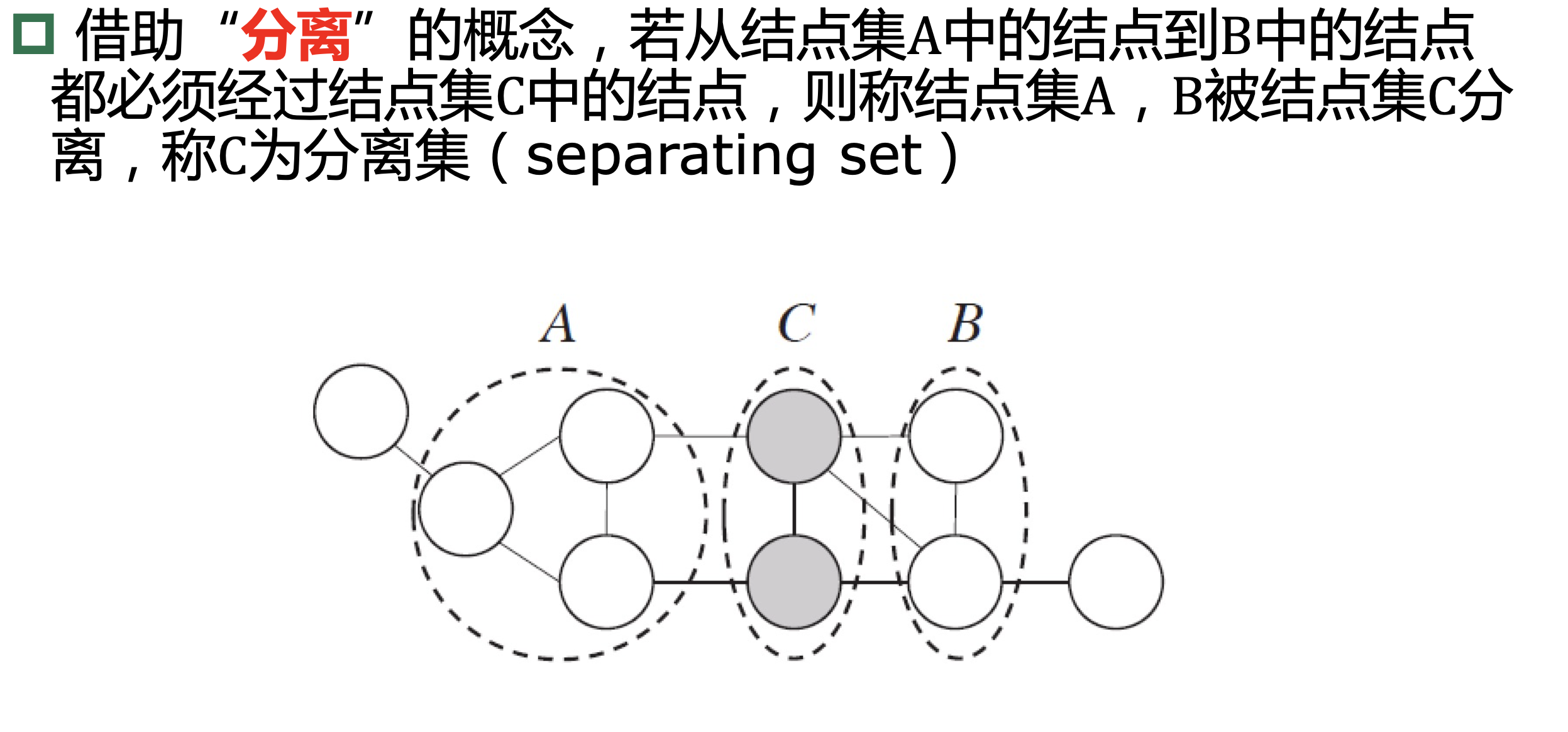
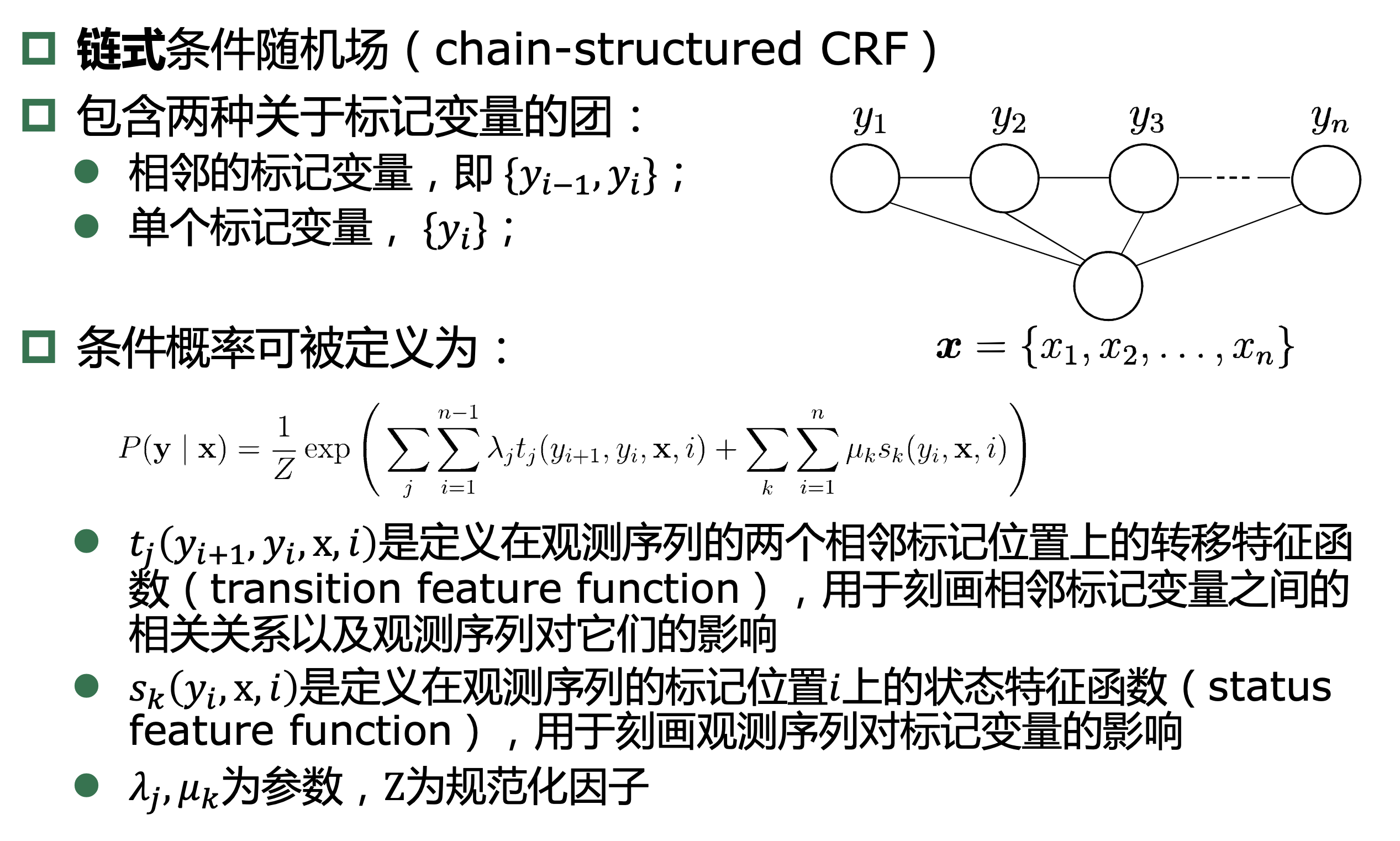
13.3、条件随机场

条件随机场是一种判别式 无向图模型(可看作给定观测值的MRF)

条件随机场对多个变量 给定相应观测值后的条件概率进行建模，若令\(x= x_1,x_2,...,x_n\)为观测序列,\(y= y_1,y_2,...,y_n\)为对应的标记序列， CRF的目标是构 建条件概率模型\(P(y|x)\)。

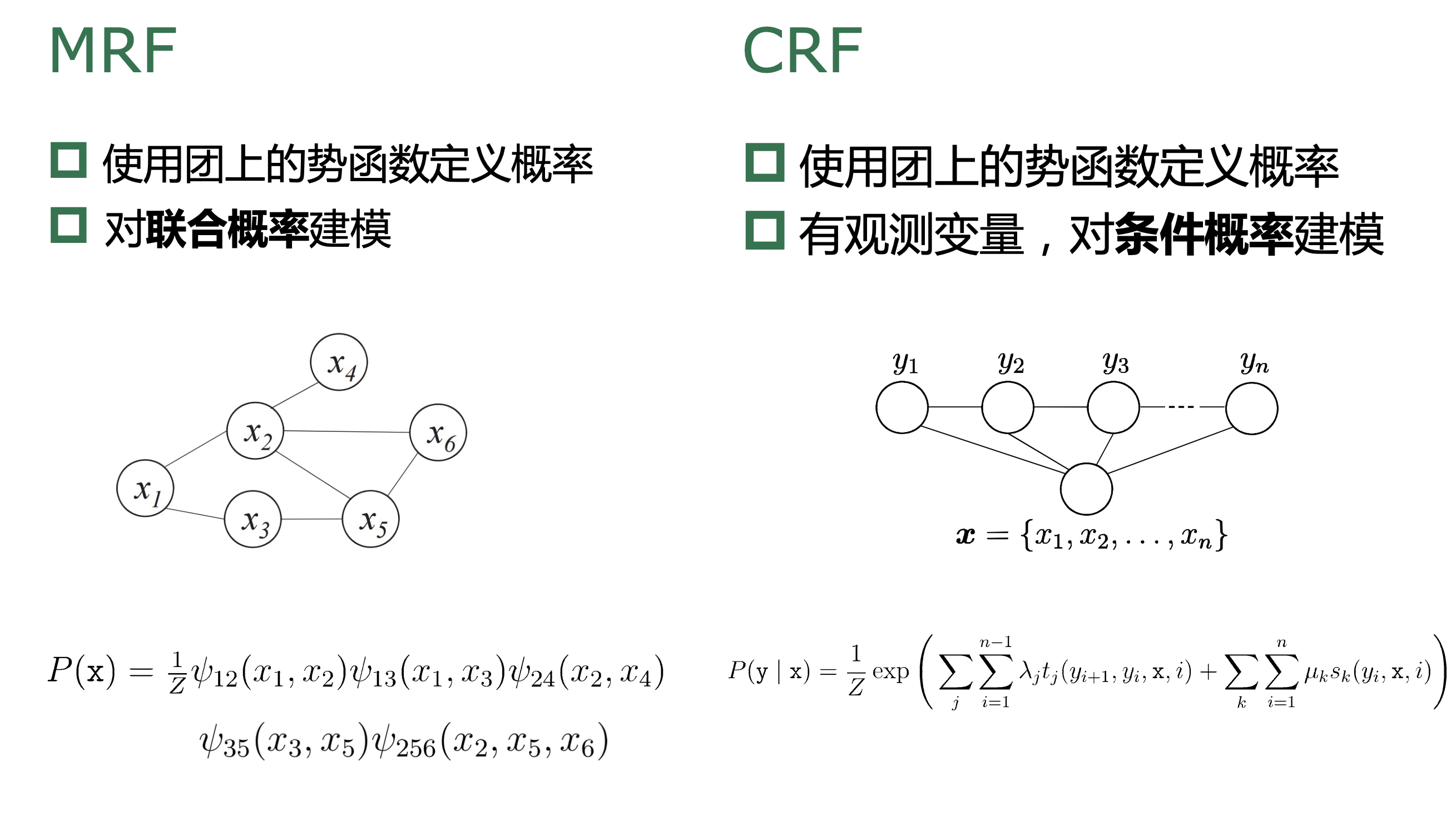
13.4、学习与推断

13.4.1、精确推断

13.4.2、信念传播

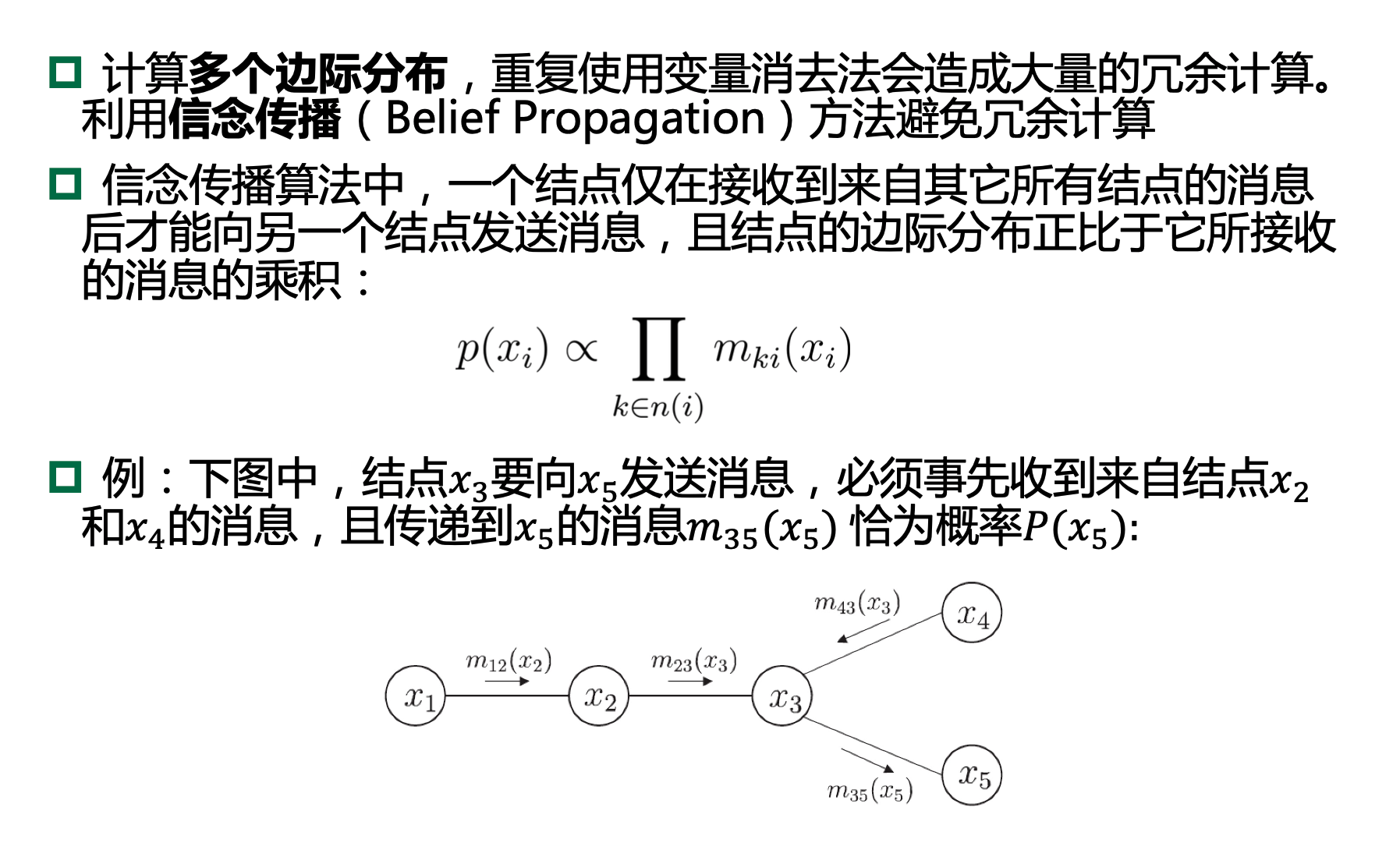
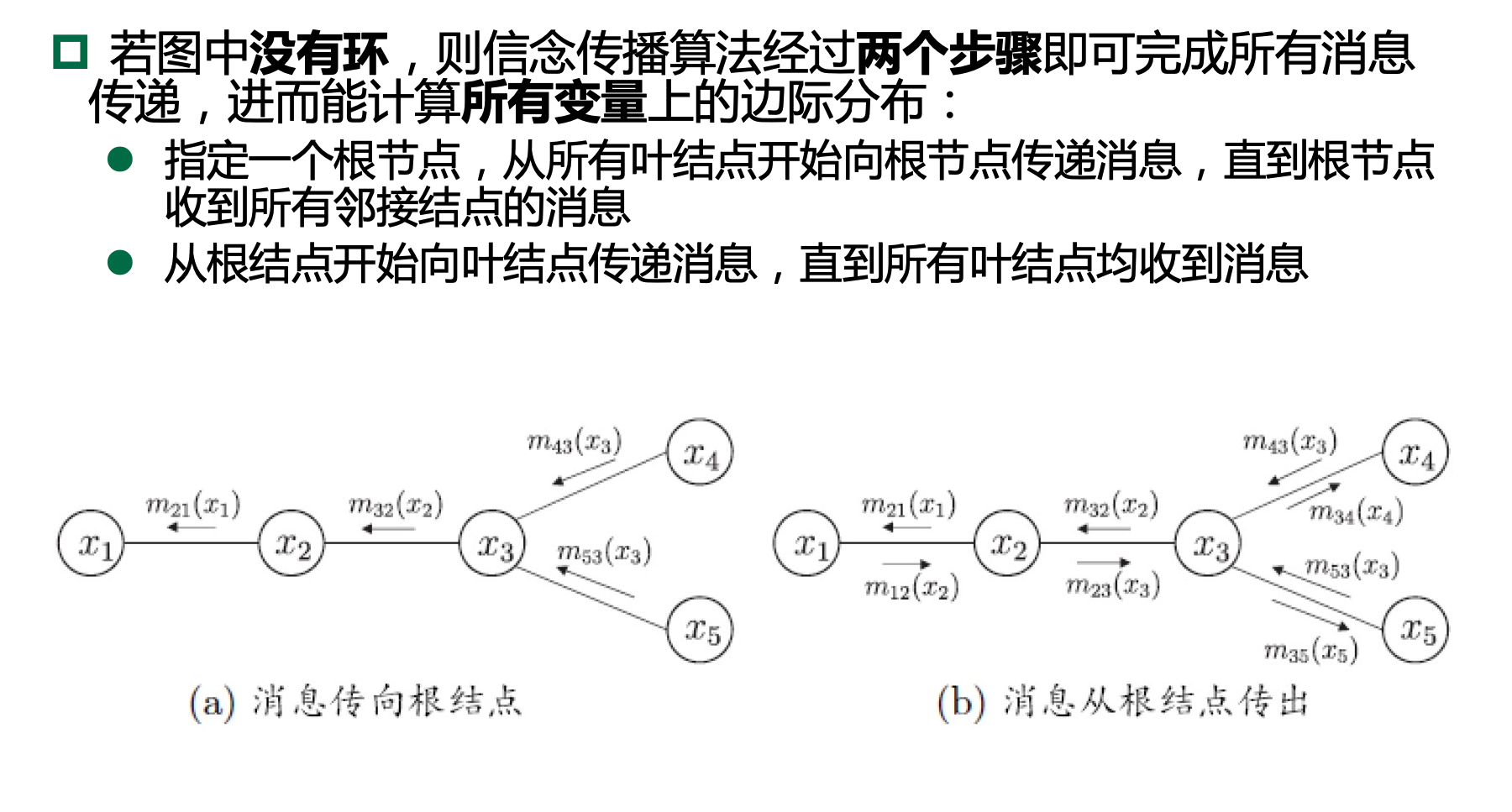
13.4.3、近似推断

采样法(sampling):通过使用随机化方法完成

在很多任务中，我们关心某些概率分布并非因为对这些概率分布本身感兴趣，而是要基于它们计算某比期望，并且还可能进一步基于这些期望做出决策.

采样法正是基于这个思路.具体来说，假定我们的目标是计算函数 f(x) 在 概率密度函数 p(x) 下的期望

\[\mathbb{E}_{p}[f]=\int f(x) p(x) d x \]

则可根据 p(x) 抽取一组样本 \(\left\{x_{1}, x_{2}, \ldots, x_{N}\right\}\)， 然后计算 f(x) 在这些样本上的均值

\[\hat{f}=\frac{1}{N} \sum_{i=1}^{N} f\left(x_{i}\right) \]

13.4.3.1、MCMC采样

马尔可夫链蒙特卡罗 (Markov Chain Monte Carlo，简称 MCMC)方法：

给定连续变量 \(x\in X\)的概率密度函数 p(x),x在区间 A 中的概率可计算为

\[P(A)=\int_{A} p(x) d x \]

若有函数 \(f: X \mapsto \mathbb{R}\), 则可计算 \(f(x)\) 的期望

\[p(f)=\mathbb{E}_{p}[f(X)]=\int_{x} f(x) p(x) d x \]

若𝑥为高维多元 变量且服从一个复杂分布，积分操作会很困难。

p MCMC先构造出服从𝒑分布的独立同分布随机变量\(\mathbf{X}_{1}, \mathbf{X}_{2}, \ldots, \mathbf{X}_{\mathbf{N}}\),再得到无偏估计

\[\tilde{p}(f)=\frac{1}{N} \sum_{i=1}^{N} f\left(x_{i}\right) \]

13.4.3.2、MH算法

13.4.4、变分推断

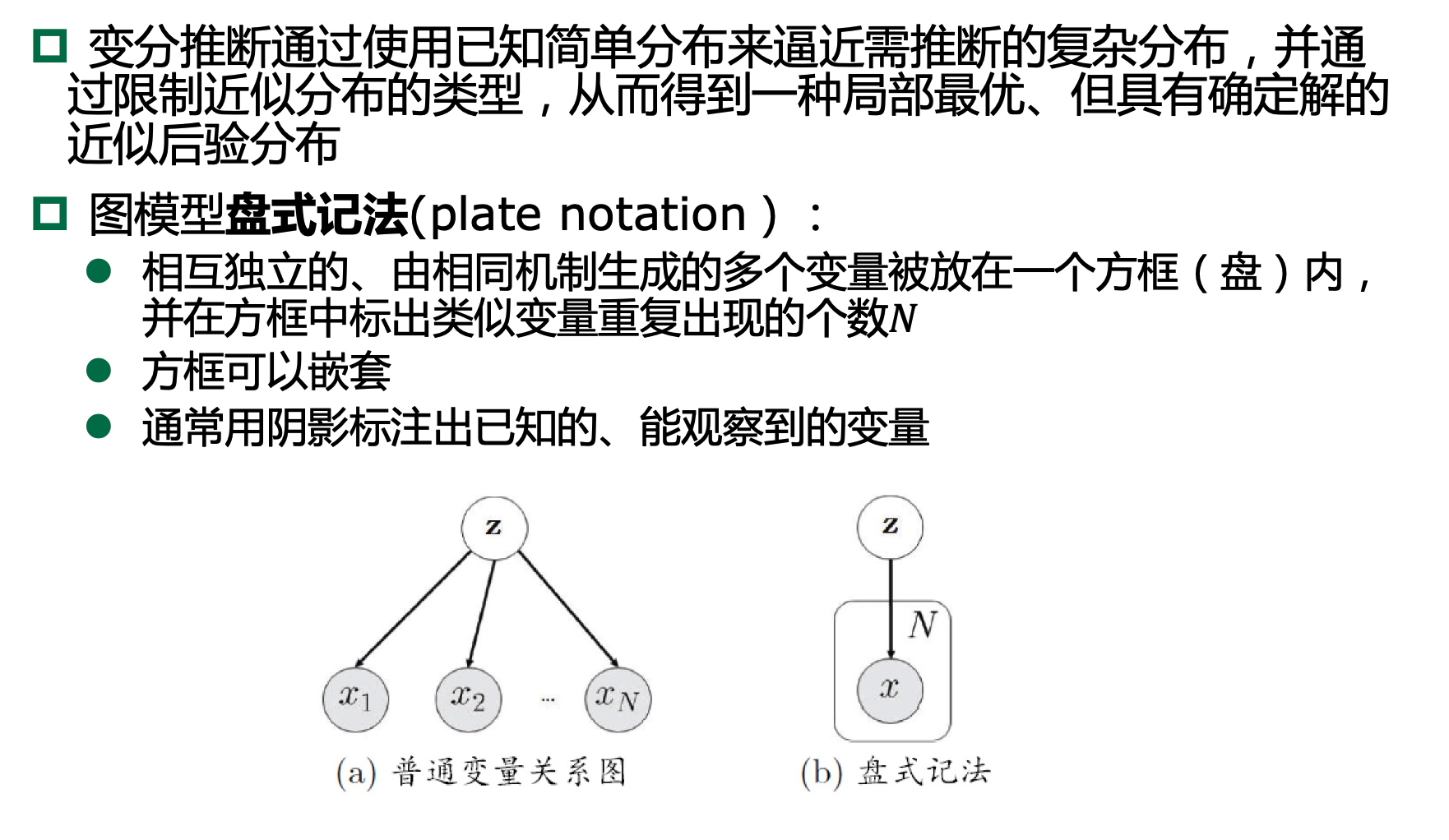
13.5、话题模型

十四、强化学习简介

14.1、MDP

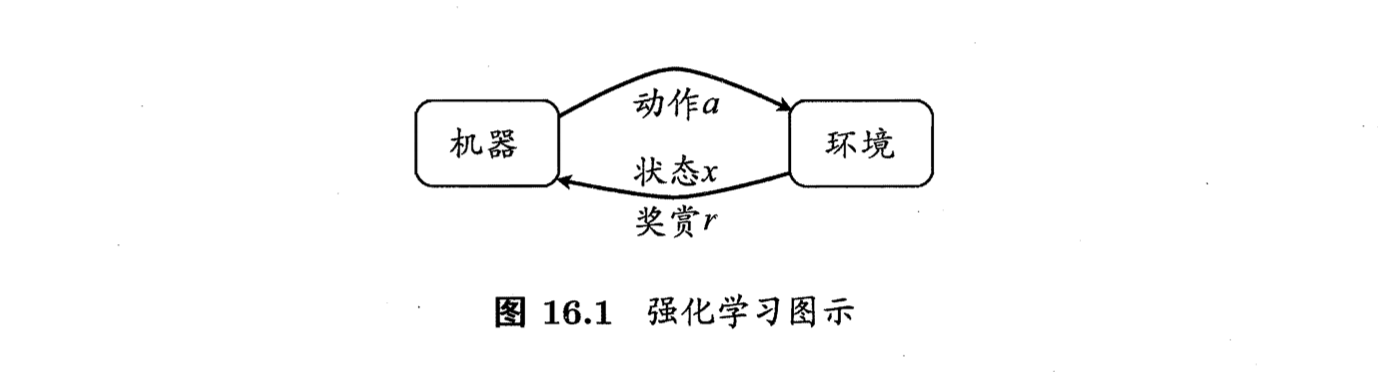
1、机器处于环境 \(E\) 中, 状态空间为 \(X\), 其中每个状态 \(x \in X\) 是机器感知到的环境的描述,

2、如在种瓜任务 上这就是当前瓜苗长势的描述; 机器能采取的动作构成了动作空间 \(A\), 如种瓜过程中有浇水、施不同的肥、使用不同的农药等多种可供选择的动作;

3、若某个 动作 \(a \in A\) 作用在当前状态 \(x\) 上, 则潜在的转移函数 \(P\) 将使得环境从当前状态 按某种概率转移到另一个状态, 如瓜苗状态为缺水, 若选择动作浇水, 则瓜苗长势会发生变化, 瓜苗有一定的概率恢复健康, 也有一定的概率无法恢复;

4、在转移 到另一个状态的同时, 环境会根据潜在的“奖赏” \((\mathrm{reward})\) 函数 \(R\) 给机器奖赏，如保持瓜苗健康对应奖赏 \(+1\), 瓜苗调零对应奖赏 \(-10\), 最终种出了 好瓜对应奖赏 \(+100 .\)

5、综合起来, 强化学习任务对应了四元组 \(E=\langle X, A, P, R\rangle\), 其中 \(P: X \times A \times X \mapsto \mathbb{R}\) 指定了状态转移概率, \(R: X \times A \times X \mapsto \mathbb{R}\) 指定了奖赏;

6、在有的应用中, 奖赏函数可能仅与状态转移有关, 即 \(R: X \times X \mapsto \mathbb{R} .\)

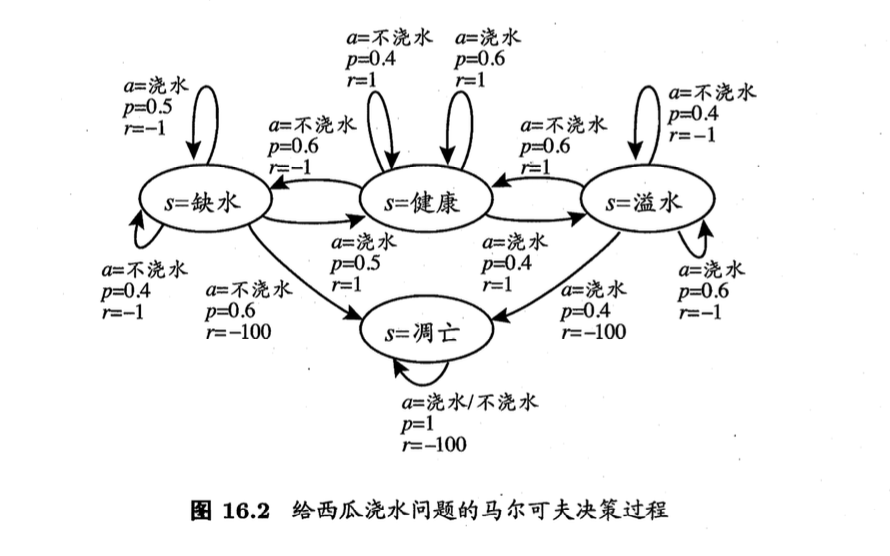
图 \(16.2\) 给出了一个简单例子：给西瓜浇水的马尔可夫决策过程。

1、该任务中只有四个状态(健康、缺水、溢水、凋亡)和两个动作(浇水、不浇水)

2、在每一步转移后，若状态是保持瓜商健康则获得奖赏 1，瓜苗缺水或溢水奖赏为-1，这时通过浇水或不浇水可以恢复健康状态，当瓜苗凋亡时奖赏是最小值 -100且无法恢复.

3、圈中箭头表示状态转移，箭头旁的 α，p，r 分别表示导致状态转移的动作、转移概率以及返回的奖赏.

4、容易看出，最优策略在"健康"状态选择动 作"浇水"、在"溢水"状态选择动作"不浇水"、在"缺水"状态选择动 作"浇水"、在"调亡"状态可选择任意动作.

1、机器要做的是通过在环境中不断地尝试而学得一个 “策略”(policy) \(\pi\)

2、根据这个策略, 在状态 \(x\) 下就能得知要执行的动作 \(a=\pi(x)\), 例如看到瓜苗状态是缺水时，能返回动作“浇水".

3、策略有两种表示方法: 一种是将策略表示为函数 \(\pi: X \mapsto A\), 确定性策略常用这种表示。

4、另一种是概率表示 \(\pi: X \times A \mapsto \mathbb{R}\), 随机性策略常用这种表示。

5、\(\pi(x, a)\) 为状态 \(x\) 下选择动作 \(a\) 的概率, 这里必须有 \(\sum_{a} \pi(x, a)=1\)。

6、策略的优劣取决于长期执行这一策略后得到的累积奖赏,例如某个策略使 得瓜苗枯死, 它的累积奖赏会很小, 另一个策略种出了好瓜, 它的累积奖赏会很大.

7、在强化学习任务中, 学习的目的就是要找到能使长期累积奖赏最大化的策 略. 长期累积奖赏有多种计算方式

8、常用的有“ \(T\) 步累积奖赏” \(\mathbb{E}\left[\frac{1}{T} \sum_{t=1}^{T} r_{t}\right]\) 和“ \(\gamma\) 折扣累积奖赏" \(\mathbb{E}\left[\sum_{t=0}^{+\infty} \gamma^{t} r_{t+1}\right]\), 其中 \(r_{t}\) 表示第 \(t\) 步获得的奖赏值, \(\mathbb{E}\) 表 示对所有随机变量求期望.