Redis源码剖析之跳表(skiplist)

最近要换新工作了，借着新老工作交替的这段窗口放松了下，所以专栏拖更了，不过我心里毫无愧疚，毕竟没人催更。不过话说回来天天追剧刷综艺的日子也很是枯燥，羡慕你们这些正常上班的人，每天都有正经工作内容，感觉你们过的很充实。[狗头]

计算机领域有很多种数据结构，数据结构的存在要么是为了节省时间、要么是为了节省空间，或者二者兼具，所以就有部分数据结构有时间换空间，空间换时间之说。其实还有某些以牺牲准确性来达到节省时间空间的数据结构，像我之间讲过的bloomfilter就是其中的典型。而今天要讲的skiplist也是一种概率性数据结构，它以一种随机概率降数据组织成多级结构，方便快速查找。

跳表

究竟何为跳表？我们先来考虑下这个场景，假设你有个有序链表，你想看某个特定的值是否出现在这个链表中，那你是不是只能遍历一次链表才能知道，时间复杂度为O(n)。
在这里插入图片描述

可能有人会问为什么不直接用连续存储，我们还能用二分查找，用链表是想继续保留它修改时间复杂度低的优势。那我们如何优化单次查找的速度？其实思路很像是二分查找，但单链表无法随机访问的特性限制了我们，但二分逐渐缩小范围的思路启发了我们，能不能想什么办法逐渐缩小范围？

我是不是可以在原链表之上新建一个链表，新链表是原链表每隔一个节点取一个。假设原链表为L0，新链表为L1，L1中的元素是L0中的第1、3、5、7、9……个节点，然后再建立L1和L0中各个节点的指针。这样L1就可以将L0中的范围缩小一半，同理对L1再建立新链表L2……，更高level的链表划分更大的区间，确定值域的大区间后，逐级向下缩小范围，如下图。
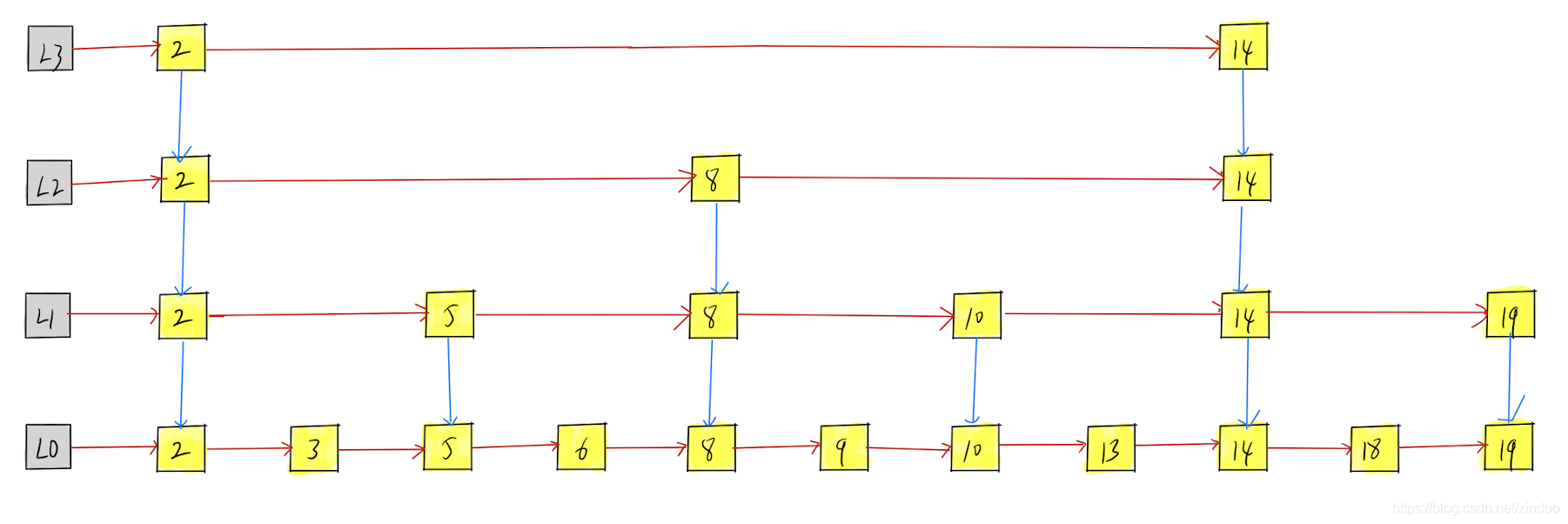
在这里插入图片描述
假设我们想找13，我们可以在L3中确定2-14的范围，在L2中确定8-14的范围，在L1中确定10-14的范围，在L0中找到13，整体寻找路径如下图红色路径，是不是比直接在L0中找13的绿色路径所经过的节点数少一些。

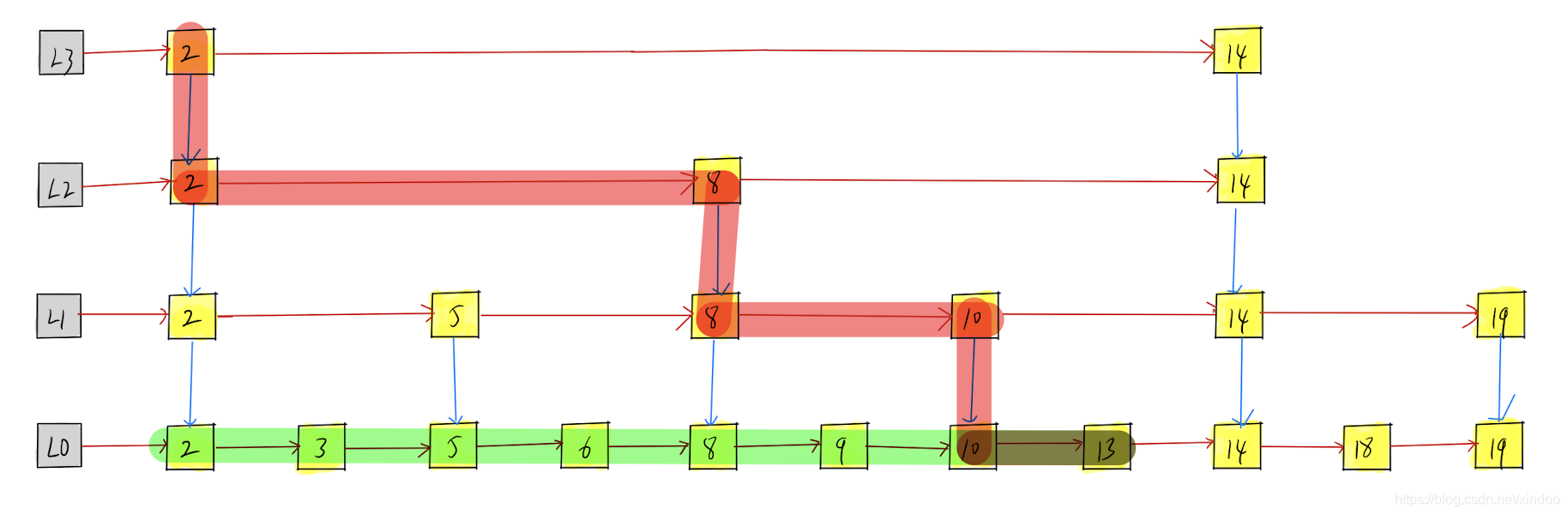
其实这种实现很像二分查找，只不过事先将二分查找的中间点存储下来了，用额外的空间换取了时间，很容易想到其时间复杂度和二分查找一致，都是O(logn)。
小伙子很牛X吗，发明了这么牛逼的数据结构，能把有序链表的查找时间复杂度从O(n)降低到O(logn)，但是我有个问题，如果链表中插入或者删除了某个节点怎么办？，是不是每次数据变动都要重建整个数据结构？
在这里插入图片描述
其实不必，我们不需要严格保证两两层级之间的二分之一的关系，只需要概率上为二分之一就行，删除一个节点好说，直接把某个层级中对应的改节点删掉，插入节点时，新节点以指数递减的概率往上层链表插入即可。比如L0中100%插入，L1中以1/2的概率插入，如果L1中插入了，L2中又以1/2的概率插入…… 注意，只要高Level中有的节点，低Level中一定有，但高Level链表中出现的概率会随着level指数递减，最终跳表可能会长这个样子。
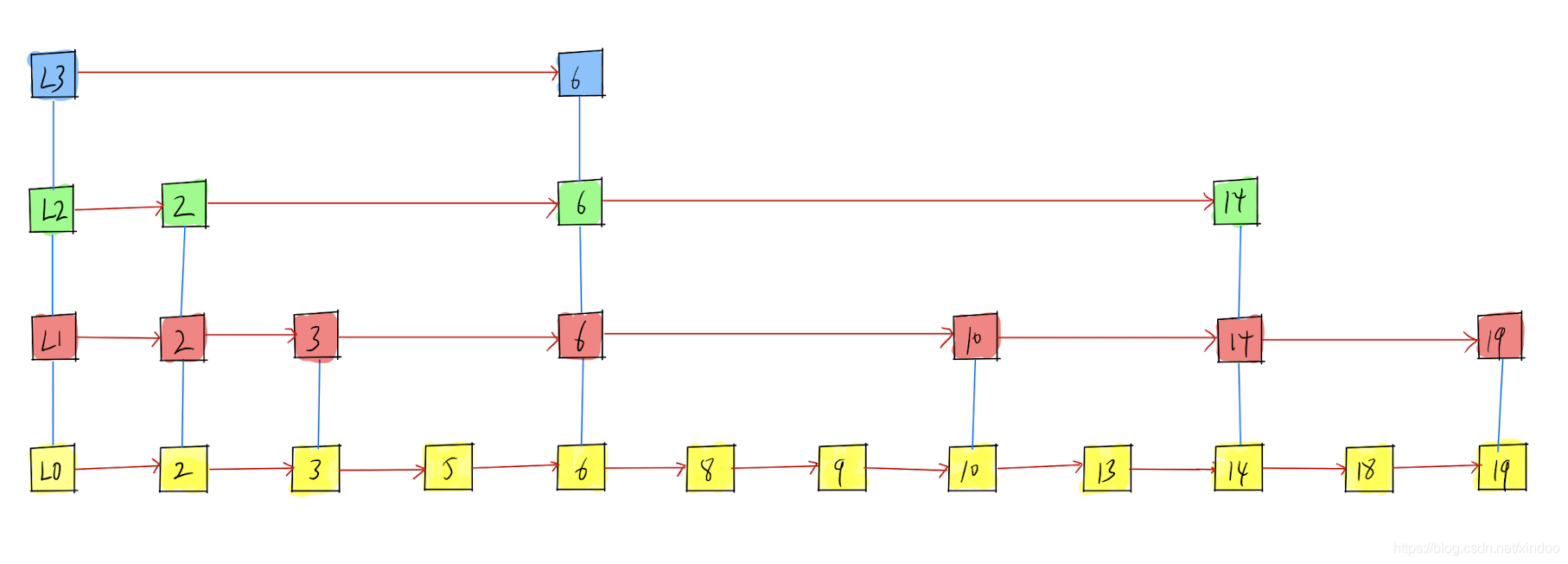
在这里插入图片描述
我们就这样重新发明了skiplist。

Redis中的跳表

Redis为了提供了有序集合(sorted set)相关的操作(比如zadd、zrange)，其底层实现就是skiplist。我们接下来看下redis是如何实现skiplist的。

typedef struct zskiplist {
    struct zskiplistNode *header, *tail; // 头尾指针 
    unsigned long length;   // skiplist的长度  
    int level;  // 最高多少级链表 
} zskiplist;

我们先来看下redis中zskiplist的定义，没啥内容，就头尾指针、长度和级数，重点还是在zskiplistNode中。zskiplistNode中是有前向指针的，所以Level[0]其实是个双向链表。

typedef struct zskiplistNode {
    sds ele;   // 节点存储的具体值 
    double score;   // 节点对应的分值 
    struct zskiplistNode *backward; // 前向指针
    struct zskiplistLevel {
        struct zskiplistNode *forward; // 每一层的后向指针 
        unsigned long span;  // 到下一个节点的跨度 
    } level[];
} zskiplistNode;

redis中的skiplist实现稍微和我们上文中讲的不大一样，它并不是简单的多级链表的形式，而是直接在zskiplistNode中的level[]将不同level的节点的关联关系组织起来，zskiplist的结构可视化如下。
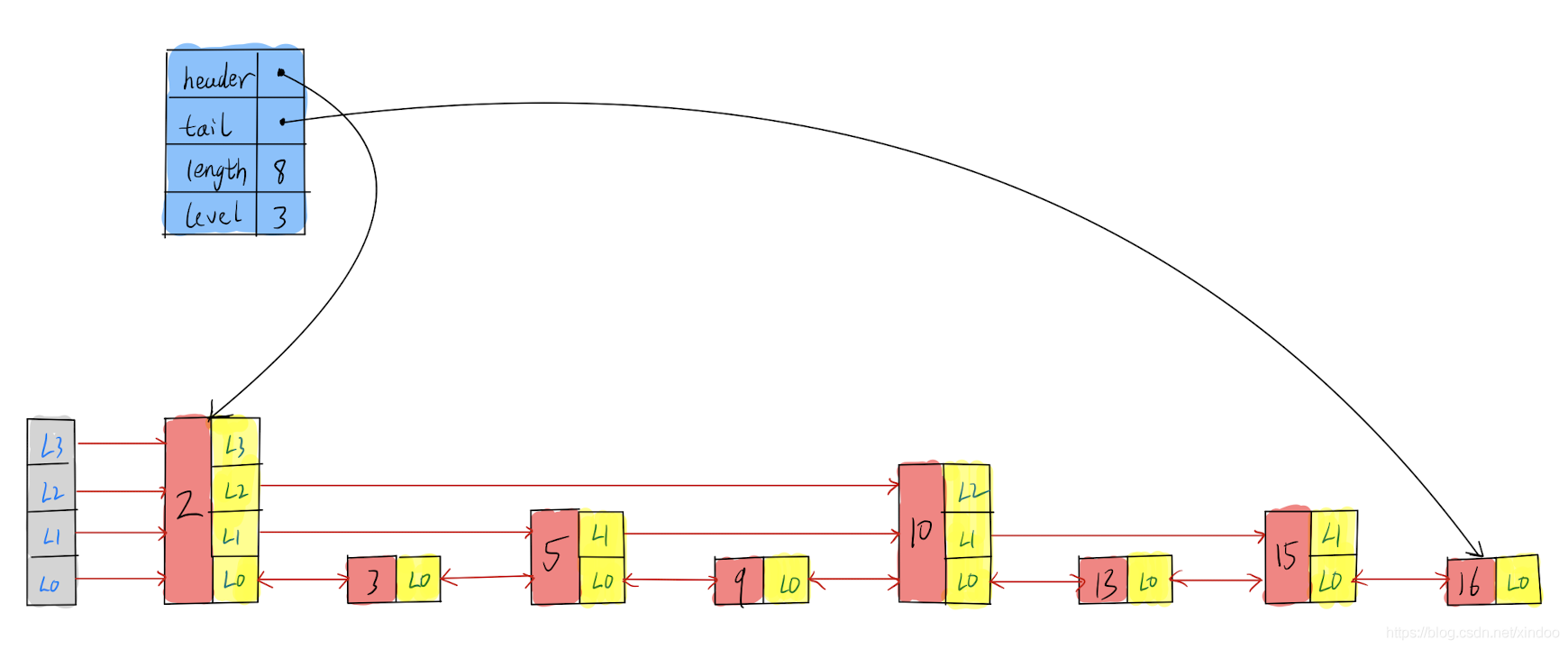
在这里插入图片描述

跳表的操作

知道了zskiplist的构造，我们来看下其几个主要操作。

新建跳表

/* 创建跳表 */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);  // 创建头节点
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

创建跳表就比较简单了，直接创建一个空的节点做为头节点。

/* 在跳表中插入一个新的节点, */
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    serverAssert(!isnan(score));
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    /* skiplist中不会出现重复的元素，但我们允许重复的分值，因为如果是调用zslInsert()的话，不会出现重复插入两
     * 个相同的元素，因为在zslInsert()中已经判断了hash表中是否存在*/
    level = zslRandomLevel();  // 生成一个随机值，确定最高需要插入到第几级链表里  
    if (level > zsl->level) {
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }
        zsl->level = level;
    }
    x = zslCreateNode(level,score,ele);  // 为插入的数据创建新节点  
    for (i = 0; i < level; i++) {
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;

        /*插入新节点后需要更新前后节点对应的span值 */
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* 为其他level增加span值，因为在原有俩节点之间插入了一个新节点 */
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    zsl->length++;
    return x;
}
int zslRandomLevel(void) {
    int level = 1;
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF)) // ZSKIPLIST_P == 0.25
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

数据插入就稍微复杂些，需要新建节点，然后确定需要在哪些level中插入新节点，还要更新前节点中各个level的span值。这里额外注意下zslRandomLevel，zslRandomLevel是以25%的概率决定是否将单个节点放置到下一层，而不是50%。

void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;
    for (i = 0; i < zsl->level; i++) {
        if (update[i]->level[i].forward == x) {
            update[i]->level[i].span += x->level[i].span - 1;  //删除节点需要修改span的值
            update[i]->level[i].forward = x->level[i].forward;
        } else {
            update[i]->level[i].span -= 1;
        }
    }
    if (x->level[0].forward) {
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;
    zsl->length--;
}

/*从skiplist中删除ele，如果删除成功返回1，否则返回0. 
 *
 * 如果节点是null，需要调用zslFreeNode()释放掉该节点，否则只是把指向sds的指针置空，这样
 * 后续其他的节点还可以继续使用这个sds*/
int zslDelete(zskiplist *zsl, double score, sds ele, zskiplistNode **node) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                     sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    /* 可能有多个节点有相同的socre，都必须找出来并删除  */
    x = x->level[0].forward;
    if (x && score == x->score && sdscmp(x->ele,ele) == 0) {
        zslDeleteNode(zsl, x, update);
        if (!node)
            zslFreeNode(x);
        else
            *node = x;
        return 1;
    }
    return 0; /* not found */
}

数据的删除也很简单，很类似于单链表的删除，但同时需要更新各个level上的数据。

其余代码就比较多，知道了skiplist的具体实现，其他相关操作的代码也就比较容易想到了，我这里就不在罗列了，有兴趣可以查阅下t_zset.c

Redis为什么使用skiplist而不是平衡树

Redis中的skiplist主要是为了实现sorted set相关的功能，红黑树当然也能实现其功能，为什么redis作者当初在实现的时候用了skiplist而不是红黑树、b树之类的平衡树？而且显然红黑树比skiplist更节省内存啊！ Redis的作者antirez也曾经亲自回应过这个问题，原文见https://news.ycombinator.com/item?id=1171423

在这里插入图片描述
我大致翻译下：

skiplist并不是特别耗内存，只需要调整下节点到更高level的概率，就可以做到比B树更少的内存消耗。
sorted set可能会面对大量的zrange和zreverange操作，跳表作为单链表遍历的实现性能不亚于其他的平衡树。
实现和调试起来比较简单。例如，实现O(log(N))时间复杂度的ZRANK只需要简单修改下代码即可。

本文是Redis源码剖析系列博文，同时也有与之对应的Redis中文注释版，有想深入学习Redis的同学，欢迎star和关注。
Redis中文注解版仓库：https://github.com/xindoo/Redis
Redis源码剖析专栏：https://zxs.io/s/1h
如果觉得本文对你有用，欢迎一键三连。
本文来自https://blog.csdn.net/xindoo

posted @ 2020-11-22 17:28 xindoo 阅读(1035) 评论(0) 编辑收藏举报

刷新页面返回顶部

xindoo

Redis源码剖析之跳表(skiplist)

跳表

Redis中的跳表

跳表的操作

新建跳表

Redis为什么使用skiplist而不是平衡树

公告