Linux OpenGL 实践篇-4 坐标系统

OpenGL坐标系　

　OpenGL中顶点经过顶点着色器后会变为标准设备坐标系。标准设备坐标系的各坐标的取值范围是[-1,1]，超过这个范围的点将会被剔除。而这个变换的过程可描述为顶点在几个坐标系统的变换，这几个坐标系统为：

模型空间（Local Sapce）
世界空间（world Space）
观察空间（View Space）
裁切空间（Clip Space）
屏幕空间（Projection Space）

　　下面我们对几个空间做一个详细的解释：　　

　　模型空间

　　表示模型最初所在的空间，即当时构建这个模型时的坐标空间。比如上一节中绘制三角形时所给的三个顶点的坐标就时模型坐标系下的坐标位置，每一个x，y，z的取值范围都是[-1,1]。

　　世界空间

　　世界坐标系描述的时所有三维模型的相对关系。

　　想象一下，我们构造模型的时候通常是一个一个的构建的，每个模型都是相对模型坐标系的（0，0，0）点进行的建模，这个时候如果我们把这些模型都放在一起，可以想象它们将叠在一起，这个当然不是我们想要的，这个时候就需要另一个坐标系来描述它们的方位关系了。比如场景中有一个人和一辆车，它们在构建时都在（0，0，0）点，现在我们在这个基础上把人放在（-2，0，0）的位置，把车放在（10，0，0）的位置，而这个坐标就是世界空间中的坐标。　　

　　观察空间

　　以摄像机在世界坐标系中的位置和方向构建的坐标系，即把世界坐标系按摄像机的位置和方向变换。

　　观察空间可以这么理解：在世界空间摆放好我们的模型之后，我们需要找一个位置和角度来观察它们，我们观察到的画面即我们要渲染的画面，而以我们眼睛为基点构建的空间即为观察空间。观察空间是把世界空间的点转换为视线前方的点的而产生的结果。它通常由一些平移和旋转矩阵组合成。

　　裁切空间

　　我们人眼的观察范围是有限的，计算机模拟人眼视野，所以OpenGL渲染的顶点应该都在一个视野范围内，这个视野范围即我们所谓的裁切空间，超出这个范围的点就被裁切掉。裁切空间定义在标准设备坐标系上的，坐标的取值范围是(-1,1)，但我们观察空间中的顶点是三维的，如果要把三维的顶点映射为二维的点，我们需要定义一个投影矩阵把观察空间的点映射到裁切空间。

　　投影就是将三维物体投射到二维平面的过程，投影可分为正投影和透视投影。

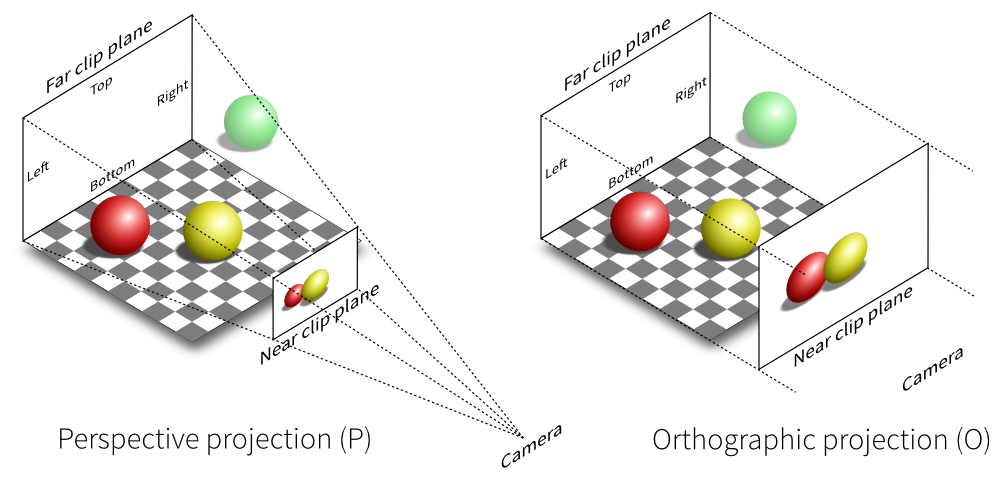
正投影

　　正投影比较简单，他的平截头体是一个长方体，在这个长方体内的顶点可见，其它点则剔除。这个长方体可以由left，right，bottom，top，near，far这几个参数确定，其中near和far表示近平面和远平面。投影可以看作是把三维画面投影在近平面，可以想象，因为远平面和近平面一样大，所以投影对于物体的大小没有影响，可以推断：在着色器使用齐次坐标，顶点着色器透视除法所使用的w为1，即（x/w,y/w,z/w,1)，w=1。

透视投影

　　在实际生活中常见的现象是离我们越远的物体越小，越近的物体越大。这个效果就是透视，最直观的现象即使两条平行线在远处会相交，如铁路上的铁轨。要实现这种透视的效果我们需要一个梯状的平截头体,这个平截头体的参数定义可同正投影使用6个参数，也可使用指定fov的方式定义。与正投影相比，透视投影的远平面更大，这样越远的物体投影到近平面时就越小，即w是一个与z相关的值。

具体的投影矩阵推导可参见：这里；

　　这里的投影其实是借助了“齐次坐标”的应用，关于“齐次坐标”，有兴趣的同学可自行google或百度。使用齐次坐标的好处就是能把三维的平移使用四维的错切变换实现，即平移可以使用矩阵的乘法实现（在三维坐标下三维平移是使用加法），这样所有的变换都可以统一为乘法，方便计算。

　　屏幕空间

　　屏幕空间可理解为显示器屏幕上定义的坐标空间，有两种定义，一种是以左上角为（0，0）点，右下角为（width，height），其中width和height是屏幕的宽和高；一种是左下角为（0，0）点，右上角为（width，height）。

　　MVP

　　MVP即我们常用的把坐标从模型坐标系变换到投影坐标系的矩阵，其中M表示model，V表示view，P表示Projection。根据前文表述，我们有4个坐标系（屏幕坐标系统除外），其中有三个变化，分别是：模型空间->世界空间，世界空间->观察空间，观察空间->裁切空间，把这3个变化矩阵组合到一起即为模型空间到裁切空间的矩阵变换——MVP：

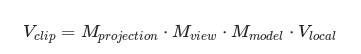
　　　 $V_{c l i p} = M_{p r o j e c t i o n} \cdot M_{v i e w} \cdot M_{m o d e l} \cdot V_{l o c a l}$

结语　　

　　为什么要分这么多个阶段的变化？为什么会有这么几个坐标系空间？

　　这些坐标系空间都是我们理解这个三维的世界时所提炼出来的概念，比如摄像机模拟的就是人的眼睛，世界坐标系则可以对标我们现实的大世界。对于这些空间坐标系划分和梳理，能够让我们直观的计算机绘制三维世界的过程，同时结合矩阵的应用，我们能够根据我们的目的选择合适的坐标系空间来操作，比如在进行物体移动的时候，使用世界坐标系会比较的方便，计算光照或投影时，在摄像机空间可能更为方便。