spark 机器学习 随机森林 原理(一)
1.什么是随机森林
顾名思义,是用随机的方式建立一个森林,森林里面有很多的决策树组成,随机森林的每一棵决 策树之间是没有关联的。在得到森林之后,当有一个新的输入样本进入的时候,就让森林中的每一棵决策树分别进行一下判断,看看这个样本应该属于哪一类(对于分类算法),然后看看哪一 类被选择最多,就预测这个样本为那一类。
我们可以这样比喻随机森林算法:每一棵决策树就是一个精通于某一个窄领域的专家(因为我们 从M个特征中选择m个让每一棵决策树进行行学习),这样在随机森林中就有了了很多个精通不不同领 域的专家,对一个新的问题(新的输入数据),可以用不不同的角度去看待它,最终由各个专家, 投票得到结果
2.Bootstraping(随机且有放回地抽取)
Leo Breiman于1994年提出的Bagging(又称Bootstrap aggregation,引导聚集)是最基本的集成技术之一。Bagging基于统计学中的bootstraping(自助法),该方法使得评估许多复杂模型的统计数据更可行。
2.1bootstrap方法的流程如下:假设有尺寸为N的样本X。我们可以从该样本中有放回地随机均匀抽取N个样本,以创建一个新样本。换句话说,我们从尺寸为N的原样本中随机选择一个元素,并重复此过程N次。选中所有元素的可能性是一样的,因此每个元素被抽中的概率均为1/N。
2.2假设我们从一个袋子中抽球,每次抽一个。在每一步中,将选中的球放回袋子,这样下一次抽取是等概率的,即,从同样数量的N个球中抽取。注意,因为我们把球放回了,新样本中可能有重复的球。让我们把这个新样本称为X1。
重复这一过程M次,我们创建M个bootstrap样本X1,……,XM。最后,我们有了足够数量的样本,可以计算原始分布的多种统计数据。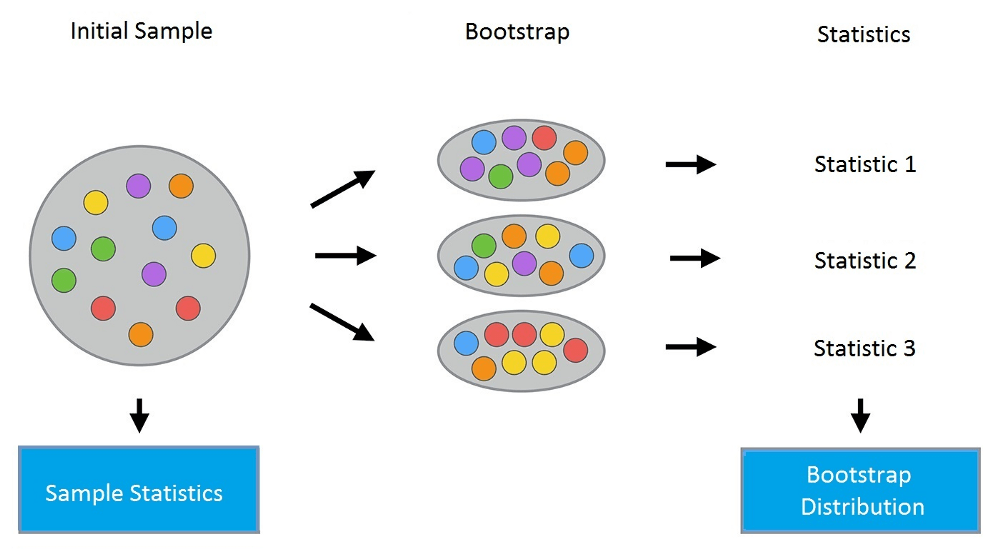
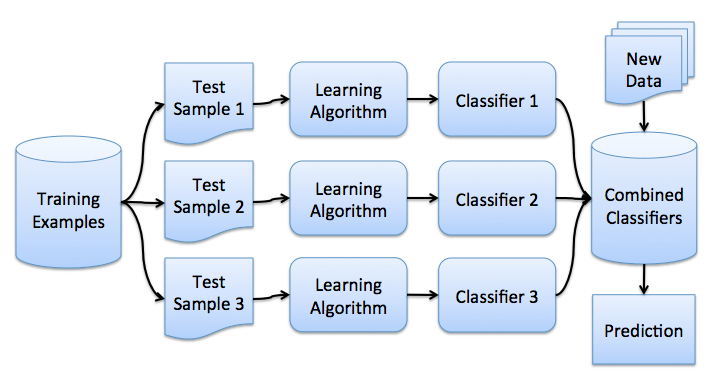
3. Bagging
理解了bootstrap概念之后,我们来介绍bagging。
假设我们有一个训练集X。我们使用bootstrap生成样本X1, …, XM。现在,我们在每个bootstrap样本上分别训练分类器ai(x)。最终分类器将对所有这些单独的分类器的输出取均值。在分类情形下,该技术对应投票(voting):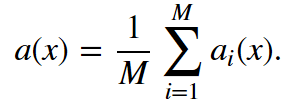
4.袋外误差(OOBE)
我们知道,在构建每棵树时,我们对训练集使用了不同的bootstrap sample(随机且有放回地抽取)。所以对于每棵树而言(假设对于第k棵树),大约有1/3的训练实例没有参与第k棵树的生成,它们称为第k棵树的oob样本。
而这样的采样特点就允许我们进行oob估计,它的计算方式如下:
1对每个样本,计算它作为oob样本的树对它的分类情况(约1/3的树);
2然后以简单多数投票作为该样本的分类结果;
3最后用误分个数占样本总数的比率作为随机森林的oob误分率。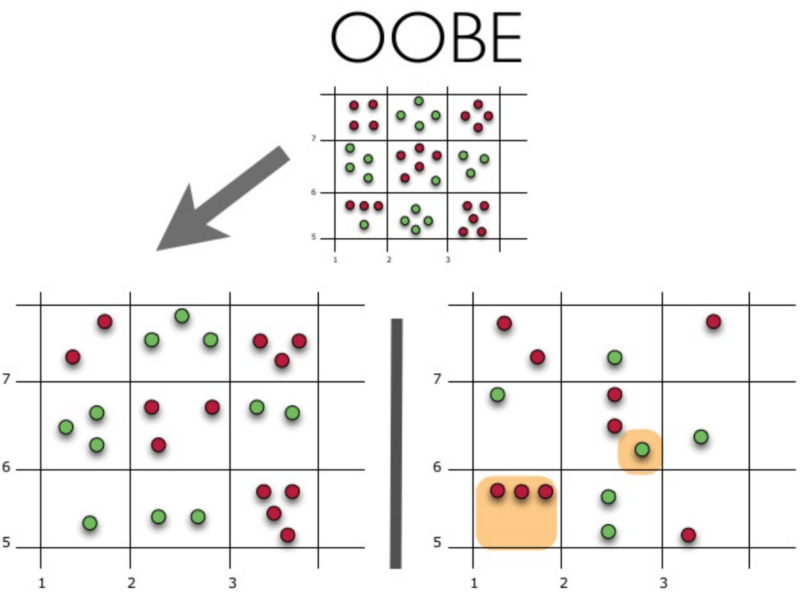
示意图上方为原始数据集。我们将其分为训练集(左)和测试集(右)。在测试集上,我们绘制一副网格,完美地实施了分类。现在,我们应用同一副网格于测试集,以估计分类的正确率。我们可以看到,分类器在4个未曾在训练中使用的数据点上给出了错误的答案。而测试集中共有15个数据点,这15个数据点未在训练中使用。因此,我们的分类器的精确度为11/15 * 100% = 73.33%.
总结一下,每个基础算法在约63%的原始样本上训练。该算法可以在剩下的约37%的样本上验证。袋外估计不过是基础算法在训练过程中留置出来的约37%的输入上的平均估计。
5.随机森林流程
5.1设样本数等于n,特征维度数等于d。
5.2选择集成中单个模型的数目M。
5.3对于每个模型m,选择特征数dm < d。所有模型使用相同的dm值。
5.4对每个模型m,通过在整个d特征集合上随机选择dm个特征创建一个训练集。
5.5训练每个模型。
5.6通过组合M中的所有模型的结果,应用所得集成模型于新输入。


