/*
动态规划和分治法相似，都是通过组合子问题的解来求解原问题。 但分治法是将
问题划分为互不相交的子问题，递归地求解子问题，再将它们的解组合起来，求出
原问题的解。与之相反，动态规划应用于子问题重叠的情况，即不同的子问题具有公共的
子问题。在这种情况下，分治法会做很多不必要的工作。
动态规划方法通常用来求解最优化问题，这类问题通常有很多可行解。我们希望寻找
具有最优值的解。
我们通常按照如下4个步骤来设计一个动态规划算法：
· 刻画一个最优解的结构特征
· 递归地定义最优解的值
· 计算最优解的值，通常采用自底向上的方法
· 利用计算出的信息构造一个最优解
钢条切割：给出一个钢条长度的价格表，根据价格表，给定一段长度为 n 的钢条，求一个
切割方案，使得收益最大。可能出现的一种特殊情况就是完全不需要切割。
*/
#include <iostream>
using namespace std;
double max(double a, double b) {
return a >= b ? a : b;
}
/*
方法一：自顶向下递归实现：伪代码
CUT-ROD(p, n)
if n == 0
return 0 // 如果长度为 0，那么收益肯定为 0
q = -∞
for i = 1 to n
q = max(q, p[i] + CUT-ROD(p, n - i))
自底向上版本
return q
这种实现方法中，CUT-ROD 反复用参数值对自身进行递归调用，即它反复求解了
相同的子问题，那么在递归调用的时候，程序的工作量就会爆炸性地增长。复杂度为 2^n
*/
double cutRod(double *table, int length) {
if (length == 0)
return 0;
double q = 0;
for (int i = 1; i <= length; ++i) {
q = max(q, table[i] + cutRod(table, length - i));
}
return q;
}
/*
使用动态规划方法求解
上面的算法称为朴素递归算法，它的效率之所以很低，就是因为重复求解相同的子问题，
因此动态规划要求仔细安排求解顺序，使得每个子问题只求解一次。那么着就需要保存结果，
在再次用到这个结果的时候就不需要重新计算而是使用查找。
当然，这样的话就需要使用额外的空间来保存计算的结果。但是一般来说这样的代价是值得的。
*/
/*
方法二：带备忘的自顶向下法：
这种方法仍然按照自然的递归形式编写过程，但过程会保存每个每个子问题的解，在需要使用一个子问
题的解的时候，先查找这个子问题的解是否已经存在。
伪代码：
MEMOIZED-CUT-ROD(p, n)
let r[0 .. n] be a new array
for i = 0 to n
r[i] = -∞
return MEMOIZED-CUT-ROD-AUX(p, n, r)
MEMOIZED-CUT-ROD-AUX(p, n, r)
if r[n] >= 0
return r[n]
if n == 0
q = 0
else q = -∞
for i = 1 to n
q = max(q, p[i] + MEMOIZED-CUT-ROD-AUX(p, n - i, r))
r[n] = q
return r[n]
MEMOIZED-CUT-ROD 函数主要进行一些初始化，因为我们已经知道结果肯定是非负的。
在 MEMOIZED-CUT-ROD-AUX 中，n 代表要求的子问题，r 数组用来记忆。这种求解方法还是
从最大问题开始逐渐将问题划分为子问题。所以称为自顶向下。
*/
double memoizedCutRodAux(double *table, int length, double *r) {
if (r[length] >= 0)
return r[length];
double q = 0;
if (length > 0) {
q = -1;
for (int i = 1; i <= length; ++i)
q = max(q, table[i] + memoizedCutRodAux(table, length - i, r));
}
r[length] = q;
return q;
}
double memoizedCutRod(double *table, int length) {
double *r = new double[length + 1];
for (int i = 1; i <= length; ++i)
r[i] = -1;
return memoizedCutRodAux(table, length, r);
}
/*
方法三：自底向上
这种方法一般需要恰当定义子问题“规模”的概念，使得任何子问题的求解都只依赖于“更小的”
子问题的求解。因而我们可以将子问题按规模排序。按照由小到大的顺序进行求解。当求解某个子问题的
时候，它所以来的那些更小的子问题都已经求解完毕，结果已经保存。这样每个子问题都只需要求解一次。
这种方法和第二中的时间复杂度是一样的，但它通常有更小的系数。
伪代码：
MEMOIZED-CUT-ROD(p, n)
let r[0 .. n] be a new array
r[0] = 0
for i = 1 to n
q = -∞
for j = 1 to i
q = max(q, p[j] + r[i - j])
r[i] = q
return r[n]
自底向上版本 MEMOIZED-CUT-ROD 采用子问题的自然顺序，过程一次求解规模为 0, 1 .. n 的子问题。
子问题图：
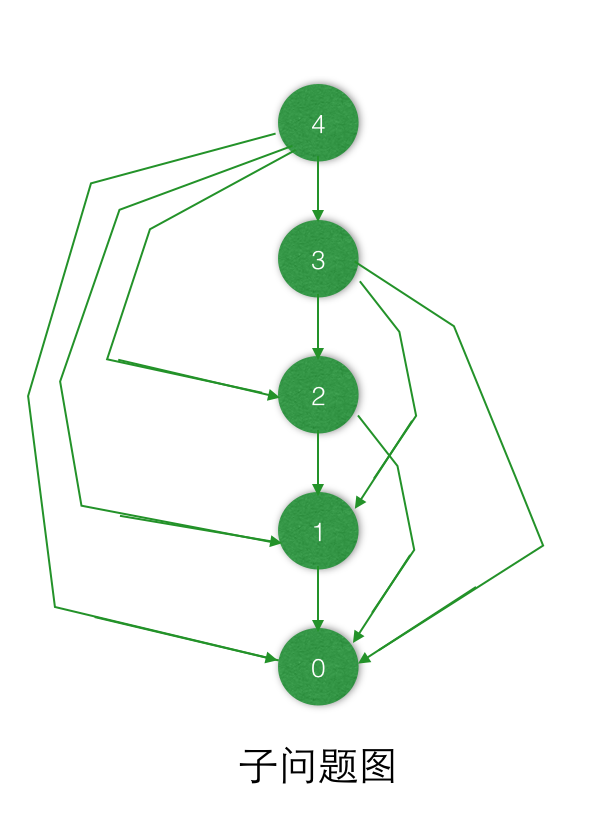自底向上动态规划是按“逆拓扑排序”或“反序的拓扑排序”来处理子问题图中的顶点。那么也就是说，对于任何一个
子问题，直至它所依赖的所有子问题均已求解完成，才会求解它。
*/
double memoizedCutRodDown(double *table, int length) {
double *r = new double[length + 1];
r[0] = 0;
double q = -1;
for (int i = 1; i <= length; ++i) {
q = -1;
for (int j = 1; j <= i; ++j) {
q = max(q, table[j] + r[i - j]);
}
r[i] = q;
}
return r[length];
}
int main(int argc, char const *argv[])
{
int steelLength;
double *table;
cout << "Input the length of the steel: ";
cin >> steelLength;
table = new double[steelLength + 1];
cout << "Input the price price table (only the price with ascending order [1 .. length]):" << endl;
for (int i = 1; i <= steelLength; ++i) {
cin >> table[i];
}
cout << "Max price(first): " << cutRod(table, steelLength) << endl;
cout << "Max price(second): " << memoizedCutRod(table, steelLength) << endl;
cout << "Max price(thied): " << memoizedCutRodDown(table, steelLength) << endl;
return 0;
}
自底向上动态规划是按“逆拓扑排序”或“反序的拓扑排序”来处理子问题图中的顶点。那么也就是说，对于任何一个
子问题，直至它所依赖的所有子问题均已求解完成，才会求解它。
