全排列，去重全排列的递归与非递归实现

全排列的概念：从n个不同元素中任取m（m≤n）个元素，按照一定的顺序排列起来，叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。

看到全排列的时候第一反应可能会是那么多情况怎么去写，就跟我们的排列组合一样。

那么要怎样处理全排列呢，我们来看一个例子：123

首先可能的排列有：123，132，  213， 231， 321， 312.我们来看看这个图：

                                                                     

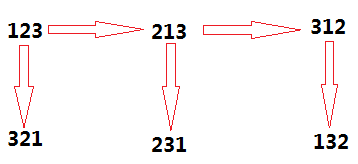
可以很直接地看到，全排列是从第一个元素开始，每个元素都和它后面的元素进行位置的互换从而得到。

所以我们就可以这样来实现：

void fullPermutation(int *arrayL, int k, int len) {
    //k是开始的下标，len代表数组的长度
    if (k== len - 1)
        output(arrayL, len);
    else {
        for (int i = k; i != len; i++) {
            swap(arrayL[i], arrayL[k]);
            fullPermutation(arrayL, k + 1, len);
            swap(arrayL[i], arrayL[k]);
        }
    }
}

我们从第一个元素开始，先交换两个元素，然后进行一次全排列，然后恢复这两个元素，因为是某个元素和它后面的元素都交换一遍，在交换的时候其他的元素位置应该是没变的。

下面是全部的实现代码：

#include <iostream>
#include <stdio.h>
#include <ctime>

using namespace std;

int count_ = 0;

void output(int* arrayL, int len) {
    for (int i = 0; i != len; i++)
        printf("%d ", arrayL[i]);
    printf("\n");
}

void swap(int& a, int& b) {
    int temp = b;
    b = a;
    a = temp;
}

void fullPermutation(int *arrayL, int k, int len) {
    //k是开始的下标，len代表数组的长度
    if (k == len - 1) {
        output(arrayL, len);
        count_++;
    }
    else {
        for (int i = k; i != len; i++) {
            swap(arrayL[i], arrayL[k]);
            fullPermutation(arrayL, k + 1, len);
            swap(arrayL[i], arrayL[k]);
        }
    }
}


int main(int argc, char const *argv[])
{
    int start = clock();
    {
        int lenOfArray;
        int *arrayL;
        printf("Enter the number lrngth of the array: ");
        scanf("%d", &lenOfArray);

        arrayL = new int[lenOfArray];
        printf("Enter the elements of the array: ");
        for (int i = 0; i != lenOfArray; i++)
            scanf("%d", &arrayL[i]);

        fullPermutation(arrayL, 0, lenOfArray);

        printf("The total seq number is: %d\n", count_);
    }
    printf("The run time: %.3lfms\n",double(clock()-start)/CLOCKS_PER_SEC);

    return 0;
}

 

因为有时候需要进行全排列的序列是有重复的，那么这个时候如果还按照上面的方法进行全排列的话，就会产生一些重复的序列，比如 1 2 2，按照上面的方法是会得到这样的序列：1 2 2， 1 2 2， 2 1 2， 2 2 1， 2 2 1， 2 1 2. 这样就不正确了。那么应该怎么去掉重复的呢？

可能开始会想到是不是遇到和自己相同的就不交换，因为交换后结果一样？的确，这个交换后结果会一样，但只是这样并不够，如122，第一个数与后面交换得212、221。然后122中第二数就不用与第三个数交换了，但对212，它第二个数与第三个数是不相同的，交换之后得到221。与由122中第一个数与第三个数交换所得的221重复了。所以这个方法不行。

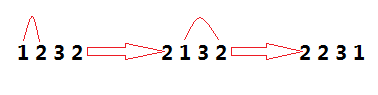
我们来看一个序列：1 2 3 2.我们用这个方法，在遇到和前面已经交换过的元素的值相同的元素就不交换，像1 2 3 2，我们在 1 和第一个 2 交换后不再和第二个 2 交换，可能你会说，2 1 3 2 和 2 2 3 1 是不一样的，怎么能不交换呢？因为如果交换的话，变成 2 2 3 1， 但 1 和第一个 2 交换后得到的序列 2 1 3 2 的1 和最后那个 2 交换后又会得到 2 2 3 1，这样就重复了。很明显，像 2 2 3 1 这样的序列会在前面的交换结果的基础上再交换得到：

                                                                                                 。

这种和字符串匹配的KMP算法有点像，重复的元素可以在前面交换的结果的基础上再交换的到。这个自己化一下应该就可以得到了。

下面是实现源码：

bool isSwap(int* arrayL, int begin, int end) {
    for (int i = begin; i != end; i++)
        if (arrayL[i] == arrayL[end])
            return false;

    return true;
}
void fullPermutation(int *arrayL, int k, int len) {
    //k是开始的下标，len代表数组的长度
    if (k == len - 1) {
        output(arrayL, len);
        count_++;
    }
    else {
        for (int i = k; i != len; i++) {
            if (isSwap(arrayL, k, i)) {
                swap(arrayL[i], arrayL[k]);
                fullPermutation(arrayL, k + 1, len);
                swap(arrayL[i], arrayL[k]);
            }
        }
    }
}

 

下面是非递归实现：...下次补充。。。