模拟退火——一种玄学算法

模拟退火介绍

模拟退火算法来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

来自百度百科

什么乱七八糟的

说白了就是求最小解。

看来学习此算法，还要学习炼钢（玩匠魂的就当我没说）。

\(\Huge \color{red} \textbf{注意！模拟退火找的是最小解！}\)

过程

选定一个温度

炼钢当然要有温度啦！（好像匠魂冶炼炉不需要设定温度，不管他了）。

我们姑且设这个温度为 \(T\) ( \(\large \textbf{T}\) \(emperature\) )。

大于边界值的处理

随机变化坐标，变化幅度为 \(T\) 。

计算新解与当前解的差 \(\delta\)。

如果新解比当前解优(\(\delta > 0\))，就用新解替换当前解。

否则以 \(e^{\frac{DE} {T}}\) 的概率用新解替换当前解。

温度乘上一个小于\(1\)的系数，即降温。

参考资料：SuperJvRuo 的博客

至于那个概率的底数为什么是\(e\)，因为概率统计中常用的正态分布中经常以\(e\)为底。（纯属猜测，就当我胡说八道吧）

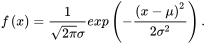
洛谷不能上传\(svg\)，这是我在这里转换的。

代码实现

const double eps=1e-14;
double xans,yans;
double ans=1e14;
void simulate_anneal(double delta,int t){
	double xx=xans;
	double yy=yans;
	while(t>eps){
		double xtemp=xans+(rand()*2-RAND_MAX)*t;
		double ytemp=yans+(rand()*2-RAND_MAX)*t;
		double new_ans=f(xtemp,ytemp);
		double DE=new_ans-ans;
		if(DE<0){
			xx=xtemp;
			yy=ytemp;
			xans=xx;
			yans=yy;
			ans=new_ans;
		}
		else if(exp(-DE/t)*RAND_MAX>rand()){
			xx=xtemp;
			yy=ytemp;
		}
		t*=delta;
	}
}

依旧参考了上述博客。

\(eps\)的设定是为了防止浮点数误差。

\(ans\)设定的初始值无所谓，只要够大就行。（因为找的是最小解）。

提示

跑模拟退火记得要多跑几次。应为模拟退火是玄学算法(使用了\(rand\))，如果自己脸不干净很容易\(\color{red}\textbf{WA}\)。

其他做法

如果单纯求最小值（极值），可以使用费马定理/罗尔定理（某些题不适用）。

若\(x\)是\(f\)函数的极值（最小值，最大值，拐点），则\(f^{'}(x)=0\)。

推荐

如果你想了解更多，可以看洛谷日报