线段树学习笔记

阅读前

By Xie Zheyuan.

这里有一份 《线段树学习笔记》 AC代码索引 里面有AC代码。

若有谬误，敬请在评论区指出。

简介

线段树是一个维护区间信息的数据结构。只要信息维护满足结合律，就可以使用线段树。

基本思路

例题

下面的思路介绍以 P3372 【模板】线段树 1 为例。

如题，已知一个数列，你需要进行下面两种操作：

• 将某区间每一个数加上 $k$。
• 求出某区间每一个数的和。

总体思路

线段树是将一个数列映射到一棵完全二叉树。其中每一个节点维护一个区间。

根节点维护 $[1,n]$，然后左子节点维护 $[1,\lfloor n \div 2 \rfloor]$，右子节点维护 $[\lfloor n \div 2 \rfloor+1,n]$。

叶子节点维护的区间左右端点相等。

我们可以用二进制表示法表示线段树，即用 $i$ 表示父节点，$2i$ 表示左子节点， $2i+1$ 表示右子节点。根节点为 $1$。这样就可以用一个组表示一棵线段树了。

所以，我们可以定义以下宏：

#define ls (i<<1) // 左子节点
#define rs (i<<1|1) // 右子节点
#define mid ((l+r)>>1) // 当前区间中部

数据上推（pushup）

原题维护的是区间和。因此我们需要将左右子树的值相加，即为父节点的值，代码如下：

void pushup(int i){
	tree[i]=tree[ls]+tree[rs];
}

时间复杂度 $O(1)$。

建树（build）

建树其实就是一个树上DFS过程。

首先，从根节点开始，向下遍历，当遇到叶子节点时，我们把它的值赋为原数组的值。

Q:那么，如何判断叶子节点，如何求出在原数组的位置呢？

A:可以在遍历时记录 $[l,r]$，表示当前遍历的区间。

所以遍历时我们需要记录三个值，$i$（当前遍历在二叉树数组的位置），$l$，$r$。

最后，遍历左右子树完成，更新当前节点，也就是 pushup。

代码如下：

void build(int i,int l,int r){
	if(l==r){
		tree[i]=a[i];
		return ;
	}
	build(ls,l,mid);
	build(rs,mid+1,r);
	pushup(i);
}

时间复杂度 $O(n)$。

没有标记的单点修改

单点修改很简单，直接在树上二分找出节点，修改后逐级 pushup 即可。

由于本题没有出现单点修改，于是不放代码了。

时间复杂度 $O(\log n)$。

区间修改-标记下传（pushdown）

区间修改肯定不是执行 $r-l+1$ 次单点修改，这样子时间复杂度 $O(n\log n)$。比暴力还慢

为了解决该问题，我们引入一个概念，懒标记（lazy tag，一般简称tag）。

我们可以在要修改的区间内打一个标记，然后访问的时候再下传就好了。

可以看出，这个操作正好与 pushup 相反，所以称之为 pushdown。

下传代码如下：

void pushdown(int i,int l,int r){
	if(tag[i]){ // 如果有标记
		tag[ls]+=tag[i]; // 左节点更新标记
		tag[rs]+=tag[i]; // 右节点更新标记
		tree[ls]+=(mid-l+1)*tag[i]; // 左节点更新值
		tree[rs]+=(r-mid)*tag[i]; // 右节点更新值
		tag[i]=0; // 清除当前节点标记
	}
}

时间复杂度 $O(1)$。

区间修改（update）

有了之前的标记下传，我们可以在树上二分 最靠近根节点的覆盖了所有修改区间的几个区间。然后打上标记。最后上传。

代码如下：

void update(int i,int l,int r,int x,int y,int k){
	if(l>=x&&r<=y){ // 被包含
		tree[i]+=(r-l+1)*k; // 修改本身的值
		tag[i]+=k; // 打标记
		return ;
	}
	pushdown(i,l,r); // 标记下传
	if(mid>=x) update(ls,l,mid,x,y,k);
	if(mid<y) update(rs,mid+1,r,x,y,k); // 二分
	pushup(i); // 上传
}

时间复杂度 $O(\log n)$。

区间查询（query）

这个比较简单，二分区间，然后统计值即可。记得要下传标记。

代码如下：

int query(int i,int l,int r,int x,int y){
	if(l>=x&&r<=y){ // 被包含
		return tree[i];
	}
	pushdown(i,l,r);// 标记下传
	int ret=0;
	if(mid>=x) ret+=query(ls,l,mid,x,y);
	if(mid<y) ret+=query(rs,mid+1,r,x,y);// 二分
	return ret;
}

时间复杂度 $O(\log n)$。

有标记单点修改单点查询

这些都是区间操作的特例，所以没什么好说的。

时间复杂度 $O(\log n)$。

总结

pushdown的规律

pushdown 在除 build 外所有需要 向下二分（递归） 的地方 之前 必须要调用。

pushup的规律

pushup 除 query 外所有需要 向下二分（递归） 的地方 之后 必须要调用。

时间复杂度

操作	时间复杂度
数据上传	$O(1)$
建树	$O(n)$
标记下传	$O(1)$
单点/区间修改	$O(\log n)$
单点/区间查询	$O(\log n)$

关于数组大小

二叉树数组、懒标记数组一律遵循 4倍空间 原则，即大小为 $4n$。（建议留一些富余）

基础线段树应用

RMQ类

P1531 I Hate It

你需要实现一个数据结构 $A[]$，长度为 $n$,有 $m$ 个操作，支持:

• Q a b，求 $\min\limits_{i=a}^{b}{A_i}$。

• C a b，将 $A[a]$ 赋为 $b$。

$0 \lt n \le 2 \times 10 ^5,0 \lt m \lt 5000$

这是一道（带修）RMQ问题，可以用线段树维护区间 $\min$，然后实现单点修改区间查询即可。

时间复杂度为 $O(n+m\log n)$。

P1198 [JSOI2008]最大数 | BZOJ1012 [JSOI2008]最大数maxnumber

你需要实现一个数据结构 $A[]$,初始为空，有 $M$ 个操作。

• Q L，查询末尾 $L(L \gt 0)$ 个数中最大的数。
• A n，将 $n+t \pmod{B}$ 添加到 $A[]$ 末尾，其中 $t$ 是最后一次 Q 操作的值（初始为 $0$），$B$ 是模数。

$1 \leq M \leq 2 \times 10^5$，$1 \leq D \leq 2 \times 10^9$

这道题仍然是一道（带修）RMQ，只是变成了维护区间 $\max$。

时间复杂度 $O(M\log M)$。

P2880 [USACO07JAN] Balanced Lineup G

你需要实现一个数据结构 $h[]$，长度为 $n$ ，有 $q$ 个询问，每个询问给出$A$ 与 $B$，求 $\max\limits_{i=A}^{B}{h[i]} - \min\limits_{i=A}^{B}{h[i]}$。

$1 \le N \le 50000,1 \le Q \le 180000$

这道题其实正解是ST表，但也不妨用线段树来维护。

这道题需要维护多个量，我们可以建两棵线段树，同时维护。

时间复杂度 $O(n+q\log n)$。

P4392 [BOI2007]Sound 静音问题

数字录音中，声音是用表示空气压力的数字序列描述的，序列中的每个值称为一个采样，每个采样之间间隔一定的时间。

很多声音处理任务都需要将录到的声音分成由静音隔开的几段非静音段。为了避免分成过多或者过少的非静音段，静音通常是这样定义的：m个采样的序列，该序列中采样的最大值和最小值之差不超过一个特定的阈值c。

请你写一个程序，检测n个采样中的静音。

列出了所有静音的起始位置i（i满足max(a[i, . . . , i+m−1]) − min(a[i, . . . , i+m−1]) <= c），每行表示一段静音的起始位置，按照出现的先后顺序输出。如果没有静音则输出NONE。

这道题也是线段树，可以用暴力建立区间来滑动求解。

时间复杂度 $O(n \log n)$。

多标记多值

P1253 [yLOI2018] 扶苏的问题

给定一个长度为 $n$ 的序列 $a$，有 $q$ 个操作，要求支持如下三个操作：

1. 给定区间 $[l, r]$，将区间内每个数都修改为 $x$。
2. 给定区间 $[l, r]$，将区间内每个数都加上 $x$。
3. 给定区间 $[l, r]$，求区间内的最大值。

对于 $100\%$ 的数据，$1 \leq n, q \leq 10^6$，$1 \leq l, r \leq n$，$op \in \{1, 2, 3\}$，$|a_i|, |x| \leq 10^9$。

这道题维护了多标记，要注意标记下传顺序。

时间复杂度为 $O(n + q\log n)$。

P2023 [AHOI2009] 维护序列 | LibreOJ#10129. 「一本通 4.3 练习 3」维护序列

有一个长为 $n$ 的数列 $\{a_n\}$，有如下三种操作形式：

1. 格式 1 t g c，表示把所有满足 $t\le i\le g$ 的 $a_i$ 改为 $a_i\times c$ ;
2. 格式 2 t g c 表示把所有满足 $t\le i\le g$ 的 $a_i$ 改为 $a_i+c$ ;
3. 格式 3 t g 询问所有满足 $t\le i\le g$ 的 $a_i$ 的和，由于答案可能很大，你只需输出这个数模 $p$ 的值。

这道题也是多标记，也要注意下传顺序。

时间复杂度为 $O(n+m\log n)$。

奇怪维护类

CodeForces718C Sasha and Array

定义 $F_i$ 为 斐波那契数列的第 $i$ 项的数。你需要实现一个数据结构 $a[]$，支持：

1 l r x：将 $[l,r]$ 的数加上 $x$。

2 l r：求 $\sum\limits_{i=l}^{r}{F_{a[i]}}$。

$1 \le n,m \le 10^{5},1 \le a[i] \le 10^{9}$

线段树维护矩阵。

$$([1\ 1] \times \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^{i-1})_{1,2} = F_i$$

时间复杂度 $O(n\log^2 n)$。

P2572 [SCOI2010] 序列操作

埋坑，下回补。

P1438 无聊的数列

维护一个数列 $a_i$，长度为 $n$，操作数为 $m$，支持两种操作：

• 1 l r K D：给出一个长度等于 $r-l+1$ 的等差数列，首项为 $K$，公差为 $D$，并将它对应加到 $[l,r]$ 范围中的每一个数上。即：令 $a_l=a_l+K,a_{l+1}=a_{l+1}+K+D\ldots a_r=a_r+K+(r-l) \times D$。

• 2 p：询问序列的第 $p$ 个数的值 $a_p$。

$0\le n,m \le 10^5,-200\le a_i,K,D\le 200, 1 \leq l \leq r \leq n, 1 \leq p \leq n$。

本题可以用线段树+差分解决。

首先，用线段树维护原序列 $a$ 的差分数组 $A$。然后执行：

$$A_l = A_l + s,A_{r+1} = A_{r+1} - e,A_{[l+1:r]}=A_{[l+1:r]}+d$$

然后直接单点查询 $p$ 即是答案。

时间复杂度 $O(n+m\log n)$

维护技巧类

P4145 上帝造题的七分钟 2 / 花神游历各国 | LibreOJ#6281. 数列分块入门 5

你需要实现一个数据结构 $a[]$，长度为 $n$，有 $m$ 个操作，支持一下操作：

• 0 l r: 将 $[l,r]$ 的数 $a[i]=\lfloor \sqrt{a[i]} \rfloor$
• 1 l r 求 $\sum\limits_{i=l}^{r}{a[i]}$

对于 $100\%$ 的数据，$1\le n,m\le 5 \times 10^5$，$1\le l,r\le n$，数列中的数大于 $0$，且不超过 $10^{12}$。

线段树好题。

本题不能打Lazy tag。只能暴力修改。注意要剪枝。

T218729 mod板 线段树

一个长度为 $n$ 的序列，支持以下操作：

• 1 x y 求 $\sum\limits_{i=x}^y a_i$

• 2 x y 将 $[x,y]$ 的数开根号并向下取整。

• 3 x y k 将 $[x,y]$ 中所有数模 $k$。

• 4 x k 将第 $x$ 个数变为 $k$。

$n \le 10^5, q\le10^5,a_i \le 10^9$

这道题同样是上面的道理，另外， $\bmod$ 操作也要特殊处理。

权值线段树

简介

权值线段树和线段树略有不同。其实就是在递归是++。

维护的是出现的次数。

可以用来维护全局第 $k$ 大/小 的问题。也可以实现逆序对。

全局第k小(P1801 黑匣子)

先离散化。

然后就建权值线段树，当然，query 要改一下。

如果左节点大于等于 $k$，那么左子树，否则右子树。

注意。右子树的 $k$ 变为 $k-t[ls]$.

感谢 @five20。

可持久化(主席树)

可持久化数组

例题(P3919 【模板】可持久化线段树 1（可持久化数组）)

你需要维护这样的一个长度为 $N$ 的数组，支持如下几种操作

1. 在某个历史版本上修改某一个位置上的值

2. 访问某个历史版本上的某一位置的值

对于100%的数据：$1 \leq N, M \leq {10}^6, 1 \leq {loc}_i \leq N, 0 \leq v_i < i, -{10}^9 \leq a_i, {value}_i \leq {10}^9$

基本思想

主席树是对线段树进行扩充。它可以实现可持久化的数据结构。

一般来说，有一棵支持单点修改的线段树，那么可以加上一些子树来保存历史信息。

就比如说这幅图：

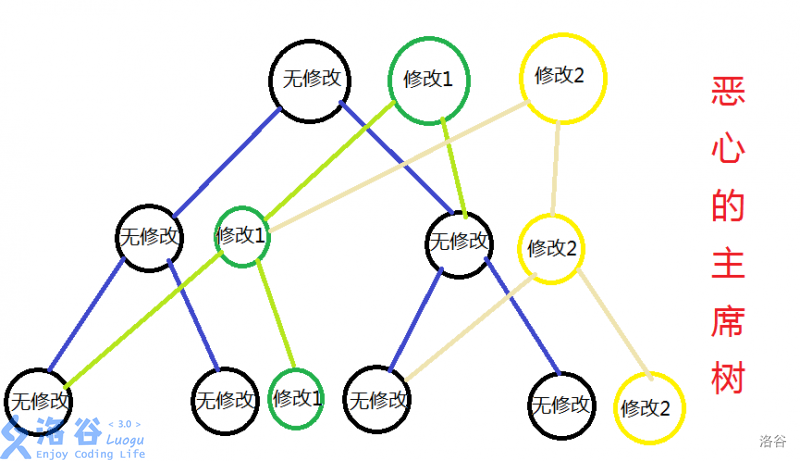
图片来源：P3919 【模板】可持久化数组 -初步探究主席树 - hyfhaha 的博客

其实，修改的历史也是一棵树。可以把它的根节点存在另外一棵类似线段树的树里。

然后就没什么好说的了，代码在索引里。有注释。

关于数组大小

主席树数组遵循 32倍空间原则。(本题数据25倍即可）

关于时间复杂度

主席树时间复杂度与一般的线段树大致相同。

可持久化权值线段树

概述

可持久化权值线段树一般应用在求静态区间第 $k$ 大/小 问题。

静态区间第k小(P3834 【模板】可持久化线段树 2)

有 $n$ 个数，$m$次询问某段区间 $[l,r]$ 中第 $k$ 小的数。

$1 \le n,m \le 2 \times 10^{5}, |a_i| \le 10^{9},1 \le l,r \le n,1 \le k \le r-l+1$

这道题是黑匣子的升级版。可以使用版本的差分思想。注意，这道题是权值线段树，不要写错了。

代码在索引里。

SP3946 MKTHNUM - K-th Number

几乎是原题。只是数据变小了(降到了 $1 \le n \le 100000, 1 \le m \le5000$)。

P3567 [POI2014]KUR-Couriers | LibreOJ#2432. 「POI2014」代理商 Couriers

给定一个长度为 $n$ 的正整数序列 $a$。共有 $m$ 组询问，每次询问一个区间 $[l,r]$ ，是否存在一个数在 $[l,r]$ 中出现的次数严格大于一半。如果存在，输出这个数，否则输出 $0$。

$1 \leq n,m \leq 5 \times 10^5$，$1 \leq a_i \leq n$。

众所周知这道题全部输出 $0$ 有 $30$ 分

挖坑，等一下埋。

线段树合并

思想

线段树合并实际上就是建立一棵线段树，维护原来两个信息的信息并。

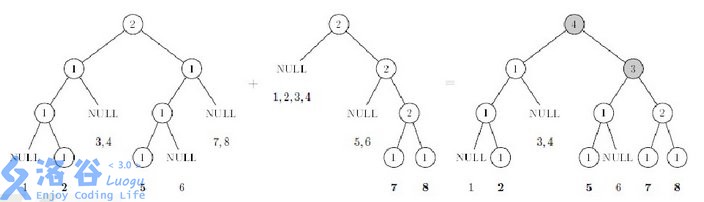
图片来源：线段树合并：从入门到放弃 - Styx 的博客 - 洛谷博客

我觉得思想很简单，直接暴力合并即可。

代码如下：

void merge(int &a,int &b){
	if(!a){
		a=b;
	}
	else if(!b){}
	else{
		t[a].v+=t[a].v;
	}
	merge(t[a].l,t[b].l);
	merge(t[a].r,t[b].r);
}

这里运用了动态开点线段树的思想，其实就是不使用传统的二进制二叉树，而是定义一个结构体保存左节点（ l），和右节点（ r ）。可以有效地减少内存 （虽然我不知道为什么）

P3224 [HNOI2012]永无乡| BZOJ2733 [HNOI2012]永无乡

永无乡包含 $n$ 座岛，编号从 $1$ 到 $n$ ，每座岛都有自己的独一无二的重要度，按照重要度可以将这 $n$ 座岛排名，名次用 $1$ 到 $n$ 来表示。某些岛之间由巨大的桥连接，通过桥可以从一个岛到达另一个岛。如果从岛 $a$ 出发经过若干座（含 $0$ 座）桥可以 到达岛 $b$ ，则称岛 $a$ 和岛 $b$ 是连通的。

现在有两种操作：(操作数为 $m$)

B x y 表示在岛 $x$ 与岛 $y$ 之间修建一座新桥。

Q x k 表示询问当前与岛 $x$ 连通的所有岛中第 $k$ 重要的是哪座岛，即所有与岛 $x$ 连通的岛中重要度排名第 $k$ 小的岛是哪座，请你输出那个岛的编号。

保证 $1 \leq m \leq n \leq 10^5$, $1 \leq q \leq 3 \times 10^5$，$p_i$ 为一个 $1 \sim n$ 的排列，$op \in \{\texttt Q, \texttt B\}$，$1 \leq u, v, x, y \leq n$。

线段树合并+并查集

如果只有操作 B ，那么不难用并查集完成。可是有了 Q 就不一样。

线段树与其他数据结构/算法的比较

树状数组

线段树和树状数组的时间复杂度大致相同。但是树状数组的常数小。

线段树比树状数组难写一些，但是树状数组的思维性更加强。

树状数组需要满足可减性，线段树不需要（这直接说明树状数组无法完成RMQ操作）。

树状数组实现逆序对等更容易，线段树需要实现权值线段树。

线段树可以方便地进行拓展，树状数组比较困难。

ST表

ST表不支持修改，线段树支持。

ST表的复杂度比线段树更加优秀。

ST表需要幂等律，线段树不需要。

线段树可以方便地进行拓展，ST表比较困难。

分块

分块复杂度不如线段树优秀。

线段树需要结合律，分块不需要。

莫队

莫队需要强制离线，线段树不需要。

莫队擅长的操作与线段树擅长的操作不一样。

线段树时间复杂度比莫队优秀。