题解P3194[HNOI2008]水平可见直线

题面

在 \(x-y\) 直角坐标平面上有 \(n\) 条直线 \(L_1,L_2,…L_n\)，若在 \(y\) 值为正无穷大处往下看，能见到 \(L_i\) 的某个子线段，则称 \(L_i\) 为可见的，否则 \(L_i\) 为被覆盖的。
例如，对于直线:
\(L_1:y=x\);
\(L_2:y=-x\);
\(L_3:y=0\);
则 \(L_1\) 和 \(L_2\) 是可见的，\(L_3\) 是被覆盖的。给出 \(n\) 条直线，表示成 \(y=Ax+B\) 的形式( $ |A|,|B| \le 500000 $ )，且 \(n\) 条直线两两不重合，求出所有可见的直线。

前置芝士：线（一次函数）的性质

\(y=Ax+B\) 中，\(A\) 与 \(B\)一个决定倾斜的程度（斜率），一个决定位置（截距）。

做法

1.排序

输入数据后，用双关键字从大到小排序，以 \(A\) 为第一关键字，以\(B\)为第二关键字。

计算相交点位置

这里有一个公式

\(P = \frac{B_1-B_2}{A_1-A_2}\)

这有什么用呢？请大家拿出一张白纸，画三条线，两两相交，然后将纸立起来，从顶部往下看（就像上帝视角那样）。如下图（这张图我是从网上下的）：

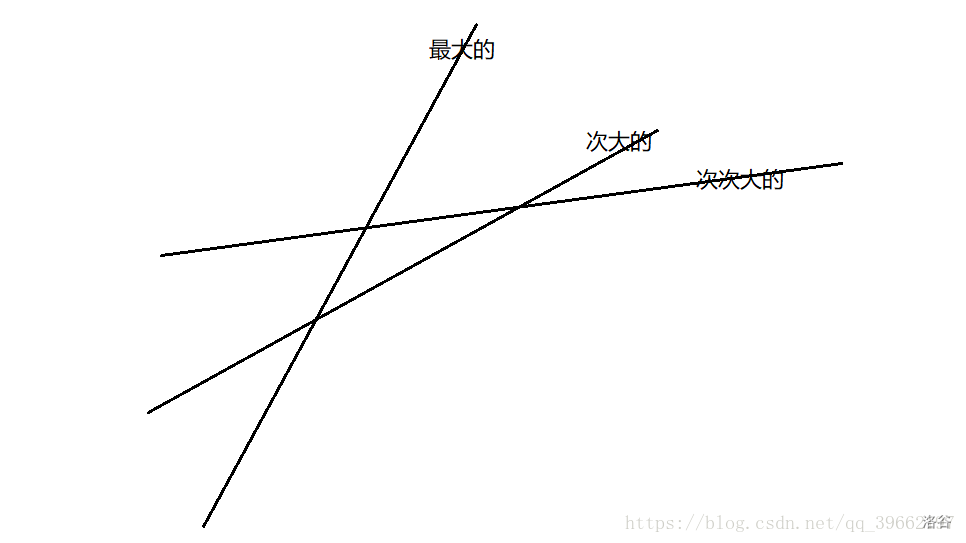
你会惊奇的发现 交点在左边的会遮住交点在右边的 ，如上图，就是次大会被遮住。

栈

然后就简单多了。按排序的顺序依次入栈，每次都检查栈顶与栈的第二个位置的交点是否在栈顶与即将入栈的左边，如果是就让栈顶元素出栈，重复直至不满足。

注意要按原来的位置输出！

代码

#include<bits/stdc++.h>
using namespace std;

int n;
struct Line{
	double a,b;
	int pos;
	const bool operator<(Line x){
		if(x.a==this->a){
			return this->b>x.b;
		}
		else{
			return this->a>x.a;
		}
	}
} lines[50005];

int sta[50005],top;

double countBanana(int x,int y){
    return (lines[x].b-lines[y].b)/(lines[y].a-lines[x].a); 
}

bool cmp(int x,int y){
	return lines[x].pos<lines[y].pos;
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%lf%lf",&(lines[i].a),&(lines[i].b));
		lines[i].pos=i;
	}
	sort(lines+1,lines+n+1);
	sta[1]=1;
	top=2;
	for(int i=2;i<=n;i++){
		if(lines[i].a==lines[i-1].a){
			continue;
		}
		while(top>=3&&countBanana(sta[top-1],sta[top-2])-countBanana(sta[top-1],i)<=(1e-8)){
			top--;
		}
		sta[top++]=i; 
	}
	sort(sta+1,sta+top,cmp);
	for(int i=1;i<=top-1;i++){
		printf("%d",lines[sta[i]].pos);
		putchar(' ');
	}
	return 1-1;
}