图论浅谈

存图

存图一般分为两种，邻接矩阵与邻接表（链式前向星）。

邻接矩阵

邻接矩阵比较简单，就是定义一个二维数组 $E$，然后 $E[i][j]$ 就是代表有一条有向边 $i \rightarrow j$。

空间复杂度为 $O(n^2)$，$n$ 为节点数。

示例代码如下：

struct MatrixGraph{
    int matrix[100][100];

    MatrixGraph(){
        memset(matrix, 0x3f, sizeof(matrix));
    }

    void add(int from,int to,int weight){
        matrix[from][to] = weight;
    }

    void add_undirected(int from,int to,int weight){
        matrix[from][to] = weight;
        matrix[to][from] = weight;
    }
};

其中 add 代表添加一个有向边 $from \rightarrow to$，而add_undirected 代表一个无向边。

邻接表

这里以链式前向星为例。

它存的是边，而边有三个属性 next , to , weight ，分别代表边的终点、边同起点的下一条边的存储位置、边权。

示例代码如下：

// 链式前向星
struct Graph{
    struct Edge{
        int next;
        int to;
        int weight;
    } edges[100];
    int head[100];
    int edge_count;

    Graph(){
        edge_count = 0; // 初始化
    }

    void add(int from,int to,int weight){
        edges[++edge_count].next=head[from];
        edges[edge_count].to=to;
        edges[edge_count].weight=weight;
        head[from]=edge_count;
    }

    void add_undirected(int from,int to,int weight){
        add(from,to,weight);
        add(to,from,weight);
    }
};

直接存储边

这个不用说了，上代码！

// 直接存边
struct EdgeGraph{
    struct Edge{
        int from;
        int to;
        int weight;
    } edges[100];
    int edge_count;

    EdgeGraph(){
        edge_count = 1;
    }
    
    void add(int from,int to,int weight){
        edges[edge_count].from=from;
        edges[edge_count].to=to;
        edges[edge_count].weight=weight;
        edge_count++;
    }

    void add_undirected(int from,int to,int weight){
        add(from,to,weight);
        add(to,from,weight);
    }
};

最短路问题

Floyed

适用存图方法：邻接矩阵

多源最短路算法，一次可以求出所有节点之间的最短路。

复杂度比较高，但是常数小，容易实现。

适用于任何图，不管有向无向，边权正负，但是最短路必须存在。（不能有个负环）

时间复杂度为 $O(n^3)$，$n$ 为节点数。经过优化的空间复杂度为 $O(n^2)$。

用DP的思想，枚举$x$到$y$的边进行计算。

状态转移方程如下：

$f[x][y] = min(f[x][y], f[x][k]+f[k][y])$

代码如下：

void floyed(int** f,MatrixGraph &g,int n){
    memcpy(f, g.matrix, sizeof(g.matrix));
    for(int k=1;k<=n;k++){
        for(int x=1;x<=n;x++){
            for(int y=1;y<=n;y++){
                f[x][y]=min(f[x][y],f[x][k]+f[k][y]);
            }
        }
    }
}

$f[x][y]$ 就是从 $x$ 到 $y$ 的最短路的权值和（说白了就是距离）

Floyed的应用——传递闭包

如果忽略权重（也就是说，将初始化的 0x3f 改为 0，连接为 1，否则为 0），Floyed的结果就是图上任意两点的连通性，这一操作名为图的传递闭包。

需要把方程改为 f[x][y] |= f[x][k] & f[k][y]。

代码如下：

void transitive_closure(int **f,MatrixGraph &g,int n){
    memcpy(f, g.matrix, sizeof(g.matrix));
    for(int k=1;k<=n;k++){
        for(int x=1;x<=n;x++){
            for(int y=1;y<=n;y++){
                f[x][y] |= f[x][k] & f[k][y];
            }
        }
    }
}

练手题目链接：洛谷B3611 【模板】传递闭包

参考代码如下：

#include <iostream>
#include <cstdio>
using namespace std;

int n;
int f[200][200];

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cin>>f[i][j];
        }
    }
    for(int k=1;k<=n;k++){
        for(int x=1;x<=n;x++){
            for(int y=1;y<=n;y++){
                f[x][y] |= f[x][k] & f[k][y];
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cout<<f[i][j];
            putchar(32);
        }
        cout<<endl;
    }
    return 0;
}

前置知识——松弛

对边$(u,v)$，松弛操作是 $dis(v)=min(dis(v),dis(u)+weight(u,v))$

其实就是DP的选择最优策略。要么不走，要么走（加上权重）。

Dijkstra

Dijkstra，读作/ˈdikstrɑ/！

算法流程

将结点分成两个集合：已确定最短路长度的点（记为 $ S $ 集合）的和未确定最短路长度的点（记为 $ T $集合）。一开始所有的点都属于 $ T $ 集合。(废话)

初始化数组 $dis[start]=0$ ，其他点的 $dis$ 均为 $\inf $。

然后重复这些操作：从
$ T $ 集合中，选取一个最短路长度最小的结点，移到$ S$
集合中。
对那些刚刚被加入 $ S $集合的结点的所有出边执行松弛操作。

直到 $T$
集合为空，算法结束。

多种实现方式

Dijkstra有许多实现方法。

暴力算法，全过程复杂度为 $O(n^2)$。
二叉堆/优先队列优化，简称堆优，全过程复杂度为 $O(m \log n)$。如果使用优先队列，则为 $O(m \log m)$
线段树优化，优化单点修改，全过程复杂度为 $O(m \log n)$。

参考代码

暴力版本（$1$为起点）

void dijkstra(int* dis,Graph &g,int n){
    const int inf = 0x3f3f3f3f;
    for(int i=1;i<=n;i++){
        dis[i]=inf;
    }
    dis[1]=0;
    for(int i=1;i<=n;i++){
        int u=0;
        for(int j=1;j<=n;j++){
            if(dis[j]<dis[u]){
                u=j;
            }
        }
        if(dis[u]==inf) break;
        for(int j=g.head[u];j;j=g.edges[j].next){
            int v=g.edges[j].to;
            if(dis[v]>dis[u]+g.edges[j].weight){
                dis[v]=dis[u]+g.edges[j].weight;
            }
        }
    }
}

堆优版本：

void heap_dijkstra(int start,int *dis,int *vis,Graph &g,int n){
    priority_queue<pair<int,int> > q;
    for(int i=1;i<=n;i++){
        dis[i]=0x3f3f3f3f;
    }
    dis[start]=0;
    q.push(make_pair(0,start));
    while(!q.empty()){
        pair<int,int> x=q.top();
        q.pop();
        int u=x.second;
        if(vis[u]) continue;
        vis[u]=1;
        for(int j=g.head[u];j;j=g.edges[j].next){
            int v=g.edges[j].to;
            if(dis[v]>dis[u]+g.edges[j].weight){
                dis[v]=dis[u]+g.edges[j].weight;
                q.push(make_pair(dis[v],v));
            }
        }
    }
}

线段树就不打了，毕竟太毒瘤了。

SPFA

SPFA死了，~~但永垂不朽！~~ 关于这个梗，请看NOI2018 Day 1 T1 归程（洛谷P4768）。

SPFA是Bellman-Ford算法的优化版本。时间复杂度为 $ O(\alpha m) $，其中 $\alpha$，是常数，一般是 $2$ ,但在毒瘤题哪里就可能退化为 $O(nm)$，应只用于有负边权的稀疏图！

有兴趣自己找资料吧，我不讲。

参考代码如下：

void spfa(int start,int *dis,int* vis,Graph &g,int n){
    for(int i=1;i<=n;i++){
        dis[i]=0x3f3f3f3f;
    }
    int u,v;
    queue<int> q;
    q.push(start);
    dis[start]=0;
    while(!q.empty()){
        u=q.front();
        q.pop();
        for(int j=g.head[u];j;j=g.edges[j].next){
            v=g.edges[j].to;
            if(dis[v]>dis[u]+g.edges[j].weight){
                dis[v]=dis[u]+g.edges[j].weight;
                if(!vis[v]){
                    vis[v]=1;
                    q.push(v);
                }
            }
        }
    }
}

最小生成树

什么是最小生成树

最小生成树（MST）为边权和最小的生成树。

只有连通图才存在生成树。

Kruskal 算法

Kruskal 算法是基于并查集、贪心的简单易写的算法。

步骤如下：

把边按照权重排序。
枚举排过序的边，如果边的左右两点的祖先不是一个（并查集实现），那么合并它们。

代码如下：

bool _kruksal_cmp(EdgeGraph::Edge a,EdgeGraph::Edge b){
    return a.weight<b.weight;
}
int find(int *fa,int x){
    if(fa[x]=x){
        return x;
    }
    else{
        return fa[x]=find(fa,fa[x]);
    }
}
int kruksal(EdgeGraph g,int n){
    int fa[n+1];;
    for(int i=1;i<=n;i++){
        fa[i]=i;
    }
    sort(g.edges+1,g.edges+g.edge_count,_kruksal_cmp);
    int ans=0;
    for(int i=1;i<=g.edge_count;i++){
        int x=find(fa,g.edges[i].from);
        int y=find(fa,g.edges[i].to);
        if(x!=y){
            ans+=g.edges[i].weight;
            fa[x]=y;
        }
    }
    return ans;
}

上面函数返回的总权值。可以用 $cnt$统计数量，当大于$n-1$时结束。

改的代码如下：

int kruksal2(EdgeGraph g,int n){
    int fa[n+1];;
    for(int i=1;i<=n;i++){
        fa[i]=i;
    }
    sort(g.edges+1,g.edges+g.edge_count,_kruksal_cmp);
    int ans=0;int cnt=0;
    for(int i=1;i<=g.edge_count;i++){
        int x=find(fa,g.edges[i].from);
        int y=find(fa,g.edges[i].to);
        if(x!=y){
            cnt++;
            ans+=g.edges[i].weight;
            fa[x]=y;
            if(cnt+1==n){
                break;
            }
        }
    }
    return ans;
}

拓扑排序

介绍

拓扑排序作用在有向无环图（Directed Acyclic Graph,简称DAG）上。

拓扑排序干了这样一件事情：如果图上有一条边 $u \rightarrow v$，那么排序后 $u$ 一定在 $v$ 前。或说是在不破坏DAG内部的顺序的前提下，将DAG拉直成一条链。

比如说下面的图：

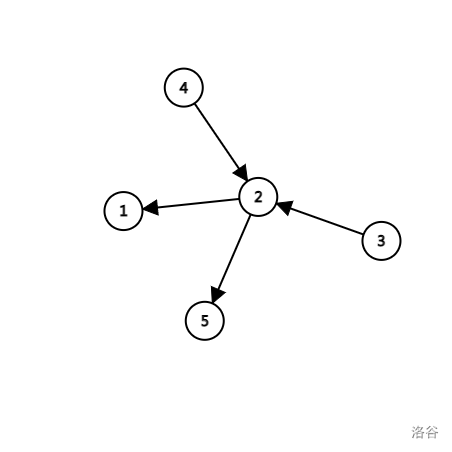
就是一个DAG。它的拓扑排序后的链是：3 4 2 1 5 (答案不唯一)

Kahn算法

Kahn算法用来求解一个DAG的拓扑排序。

步骤

首先，先删除所有入度为 $0$ 的点。如上图，就是 $3$ 与 $4$。
重复以上步骤直到图上所有点都被删除，删除的顺序就是拓扑排序的结果。

这个算法用到了一个定理：DAG删点时，整个图仍然是一个DAG。

代码如下：

void _topological_sort_dfs(int u,int *vis,int *stk,int *top,int *fa,Graph &g){
    vis[u]=1;
    for(int i=g.head[u];i;i=g.edges[i].next){
        int v=g.edges[i].to;
        if(!vis[v]){
            _topological_sort_dfs(v,vis,stk,top,fa,g);
        }
    }
    stk[++(*top)]=u;
}

void topological_sort(int *stk,Graph &g,int n){
    int vis[n+1];
    int top=0;
    int fa[n+1];
    for(int i=1;i<=n;i++){
        vis[i]=0;
    }
    for(int i=1;i<=n;i++){
        if(!vis[i]){
            _topological_sort_dfs(i,vis,stk,&top,fa,g);
        }
    }
    return ;
}

使用 int *stk 来保存结果（其实就是一个栈）

强连通分量

定义

如果在有向图中，$u$ 与 $v$ 存在一种路径，而 $v$ 与 $u$ 也存在一条路径，那么称$u$与$v$强连通。

如果任意两点都强连通，那么称这个图为强连通图。

如果一个非强连通图中存在一个最大的强连通图，那么称这个子图为 强连通分量。

比如说下图，1与2强连通，$Edge\{1,2,3\}$是强连通图，也是整个图的强连通分量。

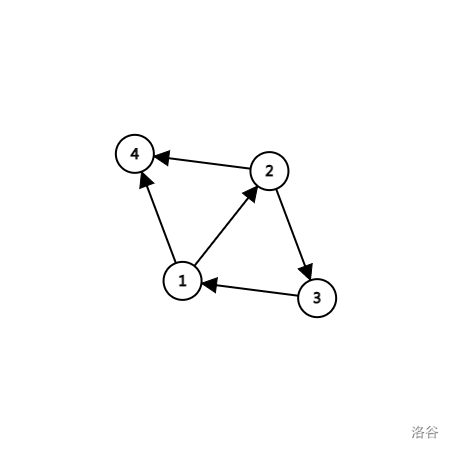
Tarjan算法

tarjan算法基于图的深度优先搜索（DFS）。每一个可能的强联通分类都是搜索树中的一棵子树。

搜索时，把当前搜索树中未处理的节点放入一个栈，回溯时判断栈顶到栈中的节点是否为一个强连通分量。

一些定义

$DFN(u)$ ：搜索到节点 $u$ 时的次序。（换句话说，就是搜索的时间戳）。

$LOW(u)$ 为 $u$ 或 $u$ 的子树能够追溯到的最早的栈中节点的次序。

步骤

当第一次搜索到点u时 $DFN[u]=LOW[u]=time$ ;
每搜索到一个点，就把该点压入栈（顶）;
当u和v有边相连时:如果v不在栈中（树枝边），搜索 $v$ 节点，并且 $LOW[u] = min\{LOW(u),LOW(v)\}$ ;如果 $v$ 在栈中（前向边/后向边），此时 $LOW[u] = min\{LOW[u],DFN[v]\}$ 。
当 $DFN[u]=LOW[u]$ 时，将它以及在它之上的元素弹出栈，此时，弹出栈的结点就构成一个强连通分量;
继续搜索，直到整张图搜索完毕。

这个算法，每条边只会遍历一次，每个点也只会遍历一次，因此如果令边数为 $n$，点数为 $m$，那么Tarjan算法的时间复杂度就是 $O(n+m)$。是一种非常高效的算法。

代码

#define MEMZERO(a) memset(a,0,sizeof(a))

void tarjan(int u,Graph &g,int N){
    int dfn[N], low[N], dfncnt=0, s[N], in_stack[N], tp=0;
    int scc[N], sc=0; 
    int sz[N]; 
    MEMZERO(dfn);
    MEMZERO(low);
    MEMZERO(s);
    MEMZERO(in_stack);
    MEMZERO(scc);
    MEMZERO(sz);
    for(int i=g.head[u];i;i=g.edges[i].next){
        const int &v=g.edges[i].to;
        if(!dfn[v]){
            tarjan(v,g,N);
            low[u]=min(low[u],low[v]);
        }
        else if(in_stack[v]){
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(dfn[u]==low[u]){
        ++sc;
        while(s[tp]!=u){
            scc[s[tp]]=sc;
            sz[sc]++;
            in_stack[s[tp]]=0;
            --tp;
        }
        scc[s[tp]]=sc;
        sz[sc]++;
        in_stack[s[tp]]=0;
        --tp;
    }
    
}

Kosaraju算法

Kosaraju算法也是基于DFS的实现。

实现方法

跑两个DFS。

第一个DFS：选取任意顶点作为起点，遍历所有未访问过的顶点，并在回溯之前给顶点编号。

第二个DFS：对于反向后的图，以标号最大的顶点作为起点开始 DFS。这样遍历到的顶点集合就是一个强连通分量。对于所有未访问过的结点，选取标号最大的，重复上述过程。

强连通分量已经找出，时间复杂度也是 $O(n+m)$。

例题大全

P5960 【模板】差分约束算法

题目传送门

题面

给出一组包含 $m$ 个不等式，有 $n$ 个未知数的形如：

\[\begin{cases} x_{c_1}-x_{c'_1}\leq y_1 \\x_{c_2}-x_{c'_2} \leq y_2 \\ \cdots\\ x_{c_m} - x_{c'_m}\leq y_m\end{cases} \]

的不等式组，求任意一组满足这个不等式组的解。

分析

乍一看以为是数学题，但看标签可知道是图论。

解一个方程组，每个方程都满足 $x_i - x_j \le c_k$，这个式子很不友好，可以化成 $x_i \le x_j + c_k$，然后就变成了一个最短路了，把 $j$ 向 $i$ 连一条有向边就可以了。
然后再建一个节点 $0$ ，连向所有边，边权为 $0$。以起点为 $0$ 跑最短路。如果有负环就输出 NO就可以了。答案是 dis 数组。

由于可能有负权边，所以用SPFA算法（是的，他没死），最坏复杂度为 $O(nm+m)=O(nm)$ 。

此即所谓差分约束算法。

哦对了，判断负权边的SPFA代码在下面，自助领取。

int tot[5005];
bool spfa(int start,int *dis,int* vis,Graph &g,int n){
	int u,v;
	queue<int> q;
	q.push(start);
	dis[start]=0;
	vis[start]=1;
	while(!q.empty()){
		u=q.front();
		vis[u]=0;
		q.pop();
		for(int j=g.head[u];j;j=g.edges[j].next){
			v=g.edges[j].to;
			if(dis[v]>dis[u]+g.edges[j].weight){
				dis[v]=dis[u]+g.edges[j].weight;
				if(!vis[v]){
					vis[v]=1;
					tot[v]++;
					if(tot[v]==n+1){
						return false;
					}
					q.push(v);
				}
			}
		}
	}
	return true;
}

代码

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

struct Graph{
	struct Edge{
		int next;
		int to;
		int weight;
	} edges[10005];
	int head[5005];
	int edge_count;
	
	Graph(){
		edge_count = 0; // 初始化
	}
	
	void add(int from,int to,int weight){
		edges[++edge_count].next=head[from];
		edges[edge_count].to=to;
		edges[edge_count].weight=weight;
		head[from]=edge_count;
	}
	
	void add_undirected(int from,int to,int weight){
		add(from,to,weight);
		add(to,from,weight);
	}
};

int n,m;
Graph g;
int tot[5005];
int Dis[5005];
int Vis[5005];

bool spfa(int start,int *dis,int* vis,Graph &g,int n){
	int u,v;
	queue<int> q;
	q.push(start);
	dis[start]=0;
	vis[start]=1;
	while(!q.empty()){
		u=q.front();
		vis[u]=0;
		q.pop();
		for(int j=g.head[u];j;j=g.edges[j].next){
			v=g.edges[j].to;
			if(dis[v]>dis[u]+g.edges[j].weight){
				dis[v]=dis[u]+g.edges[j].weight;
				if(!vis[v]){
					vis[v]=1;
					tot[v]++;
					if(tot[v]==n+1){
						return false;
					}
					q.push(v);
				}
			}
		}
	}
	return true;
}

int main(){
	memset(Dis,0x3f,sizeof(Dis));
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		g.add(0,i,0); // 初始化
	}
	for(int i=0;i<m;i++){
		int from,to,weight;
		cin>>to>>from>>weight;
		g.add(from,to,weight);
	}
	bool res = spfa(0,Dis,Vis,g,n); // 跑一遍差分约束
	if(!res)
		cout<<"NO";
	else{
		for(int i=1;i<=n;i++)cout<<Dis[i]<<" ";
	}
	cout<<endl;
	return 0;
}

参考资料

posted @ 2022-02-07 22:00 蒟蒻xiezheyuan 阅读(37) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

蒟蒻xiezheyuan

雄关漫道真如铁，而今迈步从头越。

图论浅谈

存图

邻接矩阵

邻接表

直接存储边

最短路问题

Floyed

Floyed的应用——传递闭包

前置知识——松弛

Dijkstra

算法流程

多种实现方式

参考代码

SPFA

最小生成树

什么是最小生成树

Kruskal 算法

拓扑排序

介绍

Kahn算法

步骤

强连通分量

定义

Tarjan算法

一些定义

步骤

代码

Kosaraju算法

实现方法

例题大全

P5960 【模板】差分约束算法

题面

分析

代码

参考资料

公告