算法进阶面试题07——求子数组的最大异或和（前缀树）、换钱的方法数（递归改dp最全套路解说）、纸牌博弈、机器人行走问题

主要讲第五课的内容前缀树应用和第六课内容暴力递归改动态规划的最全步骤

 

第一题

给定一个数组，求子数组的最大异或和。

一个数组的异或和为，数组中所有的数异或起来的结果。

 

简单的前缀树应用

 

暴力方法:

 

 

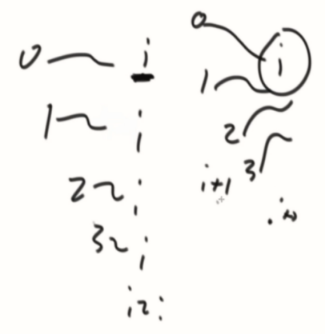
先计算必须以i结尾的子数组的异或和，然后再计算机i+1的，以此类推...

 

最暴力的解

    public static int getMaxEor1(int[] nums) {
        int maxEor = Integer.MAX_VALUE;
        for (int i = 0; i < nums.length; i++) {
            for (int start = 0; start <= i; start++) {
                int curEor = 0;
                for (int k = start; k <= start; k++) {
                    curEor ^= nums[k];
                }
                Math.max(maxEor, curEor);
            }
        }
        return maxEor;
    }

 

怎么优化？

 

异或的运算法则为：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同为0，异为1），这些法则与加法是相同的，只是不带进位，所以异或常被认作不进位加法。

0~i = eor

0~start-1 = eor2

strart~i = eor^eor2

例如

1 0 0 1 1 1 0 1 1 eor

1 0 0 1 1 0 0 0 0 eor2

0 0 0 0 0 1 0 1 1

 

优化方案，准备一个dp辅助数组记录结果。（增加空间）

    //记忆化搜索优化（利用之前的计算结果）
    public static int getMaxEor2(int[] nums) {
        int maxEor = Integer.MAX_VALUE;
        int[] dp = new int[nums.length];
        int eor = 0;
        for (int i = 0; i < nums.length; i++) {
            eor ^= nums[i];
            Math.max(maxEor,eor);
            for (int start = 0; start <= i; start++) {
                int curEor = eor ^ dp[start - 1];
                Math.max(maxEor,curEor);
            }
            dp[i] = eor;
        }
        return maxEor;
    }

 

结论：

 

 

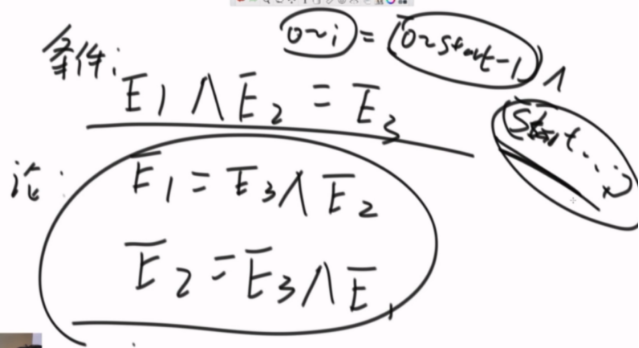
O（n）的方法

思路：求以i结尾，异或和最大的子数组。0~i、1~i、2~i全部计算出来得到结果，效率很低。

黑盒直到i，里面存了0~0、0~1、0~2...0~i-1的结果，0~i的结果在eor时刻更新的，i希望黑盒可以告诉他，这里面哪个值和eor异或出来最大，那就是答案。

例如eor和0~3异或和是最大的，那么以i结尾的，4~i就是最大的。

 

 

黑盒可以告诉你，0~start ^ eor(0~i) 是最大的，就能得出start^i是最大的。

黑盒用前缀树做，以4位二进制举例，假设0~0、0~1、0~2的值，分别加入到前缀树中

假设求以3结尾情况下，最大异或和，0~3异或结果为0010，我特别希望异或后符号位还是0，后面的尽量1，所以就在前缀树里面寻找适合的路。

 

 

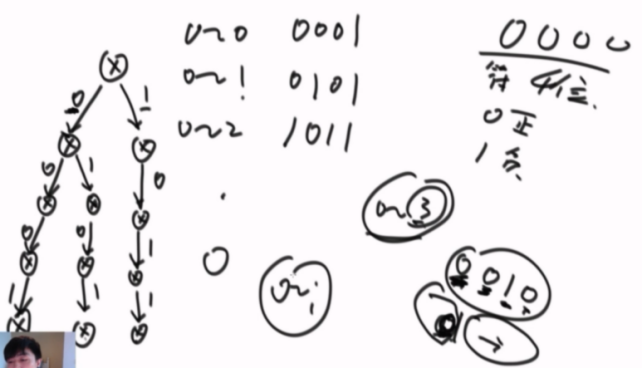
符号位尽量为0，后面的位是0走1，1走0，没得选就将就着走，尽量保持最大化值。

按前缀树的走法，每次选最优，可以找到最大值。

 

符号位为1的情况下，求补码，取反再加一

例如：

1 1 1 1

1 0 0 0 + 1

-1

1 0 1 1

1 1 0 0 + 1

-5

当符号位是1的时候，希望选1的路，让其1^1变成0，除了符号位选择的路有讲究之外，不管正负，接下来的选择是一样的，后面的位尽量都变成1。

所以选择符号位的时候，希望是和符号位的值是一样的，1选1,0选0

 

    public static class Node {//前缀树节点
        public Node[] nexts = new Node[2];//只有两个路，0/1
    }

    public static class NumTrie {//前缀树
        public Node head = new Node();

        public void add(int num) {
            Node cur = head;
            //位移，整数是31位
            for (int move = 31; move >= 0; move--) {
                //提取出每个进制里面的数字
                //例如：0101 >> 3 = 0
                //在和1进行与运算
                //0 0 0 0
                //0 0 0 1
                //0 0 0 0 //取出了第一位为0
                int path = ((num >> move) & 1);
                //查看是否有路，没有就新建
                cur.nexts[path] = cur.nexts[path] == null ? new Node() : cur.nexts[path];
                cur = cur.nexts[path];
            }
        }

        //num 0~i eor结果，选出最优再返回
        public int maxXor(int num) {
            Node cur = head;
            int res = 0;
            for (int move = 31; move >= 0; move--) {
                int path = (num >> move) & 1;
                //如果考察符号位希望和path是一样的 1^1=0 0^0=0
                //其他位置，希望是相反的 1^0=1 0^1=1
                int best = move == 31 ? path : (path ^ 1);//期待
                best = cur.nexts[best] != null ? best : (best ^ 1);//实际
                //当前位的最优选择，左移当前位的数值后，加入结果(或一下)
                res |= (path ^ best) << move;//设置每一位的答案
                cur = cur.nexts[best];//下一层
            }
            return res;
        }

    }

    public static int maxXorSubarray(int[] arr) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        int max = Integer.MIN_VALUE;
        int eor = 0;
        NumTrie numTrie = new NumTrie();
        numTrie.add(0);//0和0异或
        for (int i = 0; i < arr.length; i++) {
            eor ^= arr[i];// 0 .. i
            //这个黑盒超好用
            //放入0~i eor，返回以i结尾下最大的异或和子数组的异或值
            max = Math.max(max, numTrie.maxXor(eor));
            numTrie.add(eor);
        }
        return max;
    }

    // for test
    public static int comparator(int[] arr) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < arr.length; i++) {
            int eor = 0;
            for (int j = i; j < arr.length; j++) {
                eor ^= arr[j];
                max = Math.max(max, eor);
            }
        }
        return max;
    }

    // for test
    public static int[] generateRandomArray(int maxSize, int maxValue) {
        int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
        }
        return arr;
    }

    // for test
    public static void printArray(int[] arr) {
        if (arr == null) {
            return;
        }
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }

    // for test
    public static void main(String[] args) {
        int testTime = 500000;
        int maxSize = 30;
        int maxValue = 50;
        boolean succeed = true;
        for (int i = 0; i < testTime; i++) {
            int[] arr = generateRandomArray(maxSize, maxValue);
            int res = maxXorSubarray(arr);
            int comp = comparator(arr);
            if (res != comp) {
                succeed = false;
                printArray(arr);
                System.out.println(res);
                System.out.println(comp);
                break;
            }
        }
        System.out.println(succeed ? "Nice!" : "Fucking fucked!");
    }

 

 

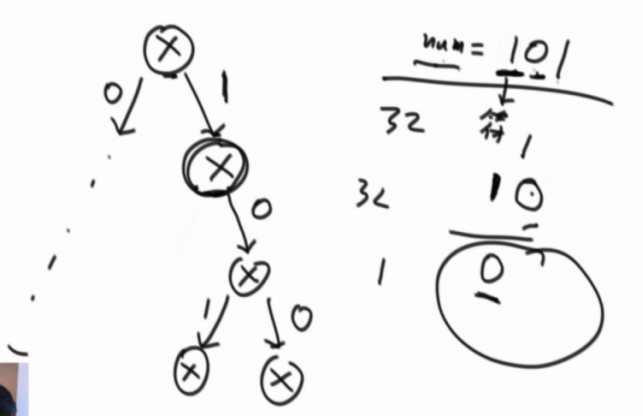
希望每次都走最优的，符号位希望是0。

 

开始第六课内容 dp最全套路解说

暴力递归怎么改动态规划（基础班最后一节有方法论的讲述）

换钱的方法数

【题目】

给定数组arr，arr中所有的值都为正数且不重复。每个值代表

一种面值的货币，每种面值的货币可以使用任意张，再给定一

个整数aim代表要找的钱数，求换钱有多少种方法。

【举例】

arr=[5,10,25,1]，aim=0。

组成0元的方法有1种，就是所有面值的货币都不用。所以返回1。

arr=[5,10,25,1]，aim=15。

组成15元的方法有6种，分别为3张5元、1张10元+1张5元、1张

10元+5张1元、10张1元+1张5元、2张5元+5张1元和15张1元。所

以返回6。

arr=[3,5]，aim=2。

任何方法都无法组成2元。所以返回0。

尝试版本写出后，后面就是搭积木。

 

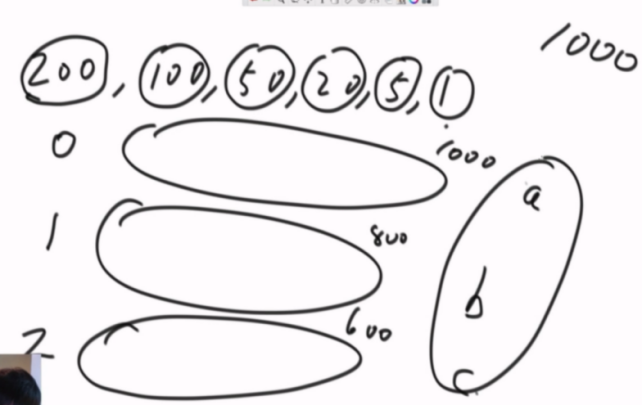
使用0张200的，后面凑出1000的方法数a

使用1张200的，后面凑出 800的方法数b

使用2张200的，后面凑出 600的方法数c

使用3张200的，后面凑出 400的方法数d

使用4张200的，后面凑出 200的方法数e

...

全部加起来就是答案。

 

    public static int coins1(int[] arr, int aim) {
        if (arr == null || arr.length == 0 || aim < 0) {
            return 0;
        }
        return process1(arr, 0, aim);
    }

    //index：任意使用index之后的所有钱
    public static int process1(int[] arr, int index, int aim) {
        int res = 0;
        if (index == arr.length) {
            res = aim == 0 ? 1 : 0;
        } else {
            for (int zhang = 0; arr[index] * zhang <= aim; zhang++) {
                res += process1(arr, index + 1, aim - arr[index] * zhang);
            }
        }
        return res;
    }

 

 

process1暴力递归方法

 

 

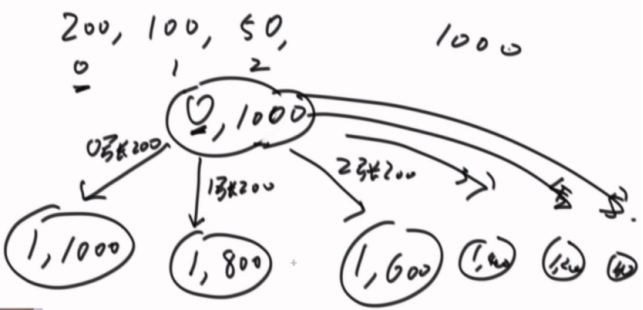
返回值一样，都要重复计算

 

 

第一个优化版本，如果index和aim固定的，只要是后面要计算600那返回值一定是确定的，是个无后效性问题，前面怎么选择不影响后面的操作。

利用一个map存储之前的结果（缓存）。下次调用，直接取出，不用这么暴力的重复计算。（记忆化搜索）

 

    //--map优化版本
    //key index_aim
    //value 组合数
    public static HashMap<String, Integer> answer = new HashMap<>();

    public static int processMap(int[] arr, int index, int aim) {
        int res = 0;
        if (index == arr.length) {
            res = aim == 0 ? 1 : 0;
        } else {
            for (int zhang = 0; arr[index] * zhang <= aim; zhang++) {
                int nextAim = aim - arr[index] * zhang;
                String nextCalc = (index + 1) + "_" + nextAim;
                if (answer.containsKey(nextCalc)) {
                    res += answer.get(nextCalc);
                } else {
                    res += processMap(arr, index + 1, nextAim);
                }
            }
        }
        answer.put(index + "_" + aim, res);
        return res;
    }

 

 

接下来直接计算所有的变化（dp），准备一个二维表 0~n是index的长度，n是终止位置。

可以装下所有返回值。

 

 

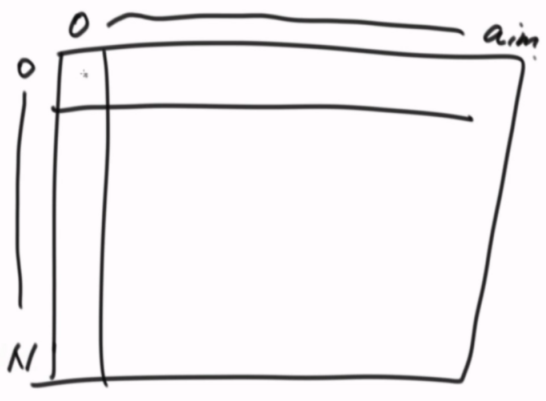
最终需要得到0 aim的值

 

 

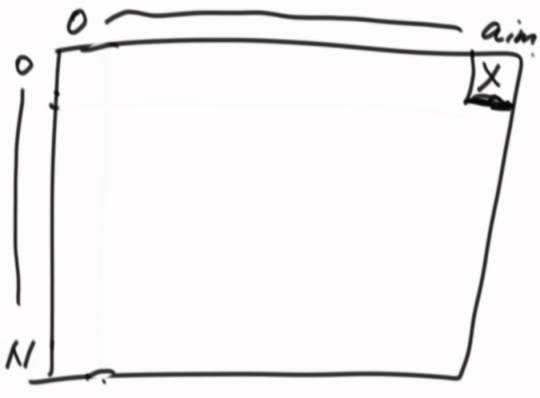
接下来思考一下，哪些位置的值是可以直接确定的，不依赖其他位置的（看递归中的basekey）

 

 

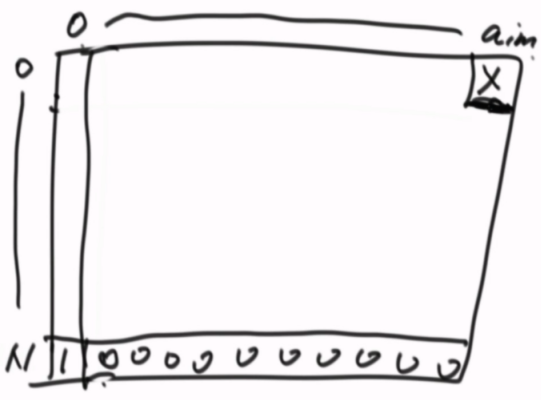
接着开始看位置依赖，也就是怎么调用递归的

index + 1, aim - arr[index] * zhang

一个具体的[index,aim]位置，需要他的下一行（假设是五块）

Aim - 0张5块、1张5块、2张5块...一直到越界的所以位置累加起来，就是他的值。

和题目已经没什么关系，就是看递归函数可以画出这个图。

 

 

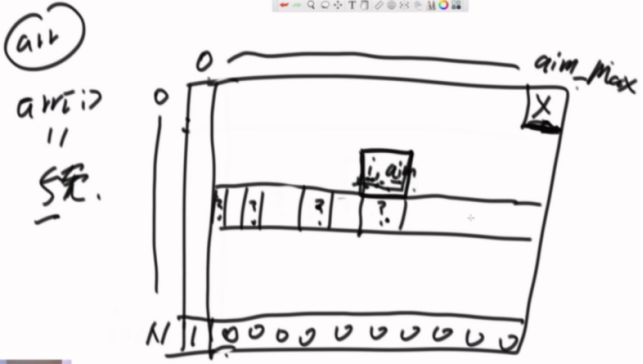
从最后一行逐行逐个推算，可以算出最后的答案就是，他的下面+下面位置-5+下面位置-5*2...一直到越界，因为最上面一列的金额数是5，所以最后结果是1+1+2=4。

 

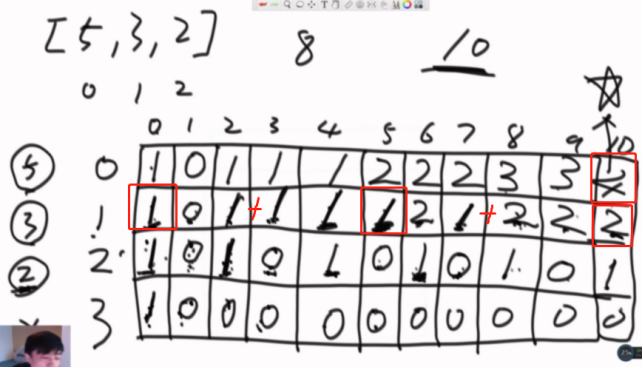
    public static int coins3(int[] arr, int aim) {
        if (arr == null || arr.length == 0 || aim < 0) {
            return 0;
        }
        int[][] dp = new int[arr.length][aim + 1];
        for (int i = 0; i < arr.length; i++) {
            dp[i][0] = 1;
        }
        for (int j = 1; arr[0] * j <= aim; j++) {
            dp[0][arr[0] * j] = 1;
        }
        int num = 0;
        for (int i = 1; i < arr.length; i++) {
            for (int j = 1; j <= aim; j++) {
                num = 0;
                for (int k = 0; j - arr[i] * k >= 0; k++) {
                    num += dp[i - 1][j - arr[i] * k];
                }
                dp[i][j] = num;
            }
        }
        return dp[arr.length - 1][aim];
    }

 

最后一步的优化（建立起空间感后）

计算A，需要对B12345进行累加，其实A的前三个位置的同层C，已经计算过12345，那其实只需要进行C+B就行。

 

 

二维三维四维问题完全一样。

 

    public static int coins4(int[] arr, int aim) {
        if (arr == null || arr.length == 0 || aim < 0) {
            return 0;
        }
        int[][] dp = new int[arr.length][aim + 1];
        //填好可以直接设置的值
        for (int i = 0; i < arr.length; i++) {
            dp[i][0] = 1;
        }
        //例如第一行是5，那么5、10、15...位置肯定为1
        for (int j = 1; arr[0] * j <= aim; j++) {
            dp[0][arr[0] * j] = 1;
        }
        //代码实现是从表格的上往下填
        for (int i = 1; i < arr.length; i++) {
            for (int j = 1; j <= aim; j++) {
                dp[i][j] = dp[i - 1][j];//每个位置一定包含下面的和
                //加上左边的位置。
                dp[i][j] += j - arr[i] >= 0 ? dp[i][j - arr[i]] : 0;
            }
        }
        return dp[arr.length - 1][aim];
    }

    //最优解，连dp都是一维的，现在理解起来有点超自然
    public static int coins5(int[] arr, int aim) {
        if (arr == null || arr.length == 0 || aim < 0) {
            return 0;
        }
        int[] dp = new int[aim + 1];
        for (int j = 0; arr[0] * j <= aim; j++) {
            dp[arr[0] * j] = 1;
        }
        for (int i = 1; i < arr.length; i++) {
            for (int j = 1; j <= aim; j++) {
                dp[j] += j - arr[i] >= 0 ? dp[j - arr[i]] : 0;
            }
        }
        return dp[aim];
    }

    public static void main(String[] args) {
        int[] coins = {10, 5, 1, 25};
        int aim = 2000;

        long start = 0;
        long end = 0;
        start = System.currentTimeMillis();
        System.out.println(coins1(coins, aim));
        end = System.currentTimeMillis();
        System.out.println("cost time : " + (end - start) + "(ms)");

        start = System.currentTimeMillis();
        System.out.println(coinsOther(coins, aim));
        end = System.currentTimeMillis();
        System.out.println("cost time : " + (end - start) + "(ms)");

        aim = 20000;

        start = System.currentTimeMillis();
        System.out.println(coins2(coins, aim));
        end = System.currentTimeMillis();
        System.out.println("cost time : " + (end - start) + "(ms)");

        start = System.currentTimeMillis();
        System.out.println(coins3(coins, aim));
        end = System.currentTimeMillis();
        System.out.println("cost time : " + (end - start) + "(ms)");

        start = System.currentTimeMillis();
        System.out.println(coins4(coins, aim));
        end = System.currentTimeMillis();
        System.out.println("cost time : " + (end - start) + "(ms)");

        start = System.currentTimeMillis();
        System.out.println(coins5(coins, aim));
        end = System.currentTimeMillis();
        System.out.println("cost time : " + (end - start) + "(ms)");

    }

 

 

之前是通过递归获取值，现在是在dp里面获取值。

 

解决类似题目：

排成一条线的纸牌博弈问题

【题目】

给定一个整型数组arr，代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌，规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A和玩家B都绝顶聪明。请返回最后获胜者的分数。

【举例】

arr=[1,2,100,4]。

开始时玩家A只能拿走1或4。如果玩家A拿走1，则排列变为[2,100,4]，接下来玩家B可以拿走2或4，然后继续轮到玩家A。如果开始时玩家A拿走4，则排列变为[1,2,100]，接下来玩家B可以拿走1或100，然后继续轮到玩家A。玩家A作为绝顶聪明的人不会先拿4，因为拿4之后，玩家B将拿走100。所以玩家A会先拿1，让排列变为[2,100,4]，接下来玩家B不管怎么选，100都会被玩家A拿走。玩家A会获胜，分数为101。所以返回101。

arr=[1,100,2]。

开始时玩家A不管拿1还是2，玩家B作为绝顶聪明的人，都会把100拿走。玩家B会获胜，分数为100。所以返回100。

 

 

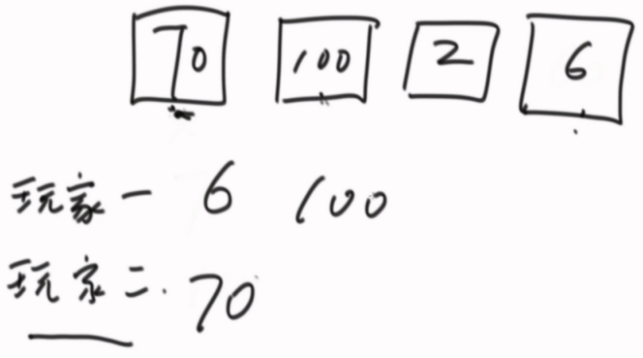
先想暴力，加入缓存，建立空间感，再改动态规划。

练递归，学习怎么去试。底下的优化全都是套路。

 

分析:  f(i, j) 表示 在arr[i~j]中A 先手时能够获得的最大分数，s(i, j) 表示 A后手时能够获得的最大分数。

首先分析f(i, j)。 A可先取arr[i], 取完后剩余arr[i+1, j]。此时相当于A后手在[i+1, j]的情况了。

也可先取arr[j], 取完后剩余arr[i, j - 1]。 此时相当于A后手在[i, j -1]的情况了。

则 f(i, j) = max{arr[i] + s(i+1, j), arr[j] + s(i, j-1)}

再分析s（i, j）。B可先取arr[i] 或 arr[j] 。取完后相当于A先手的情况了。只是在这种情况下，B会留下最差解。

s(i, j) = min{arr[i] + f(i+1, j), arr[j] + f(i, j-1)};

 

    public static int win1(int[] arr) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));
    }

    public static int f(int[] arr, int i, int j) {//先拿的
        //如果i == j，即arr[i...j]上只有一张纸牌，当然会被先拿纸牌的人拿走，所以可以返回arr[i];
        if (i == j) {
            return arr[i];
        }
        //拿了其中一个之后，当前玩家成了后拿的那个人
        //因为当前的玩家会做出最好的选择，所以会拿走最好的
        return Math.max(arr[i] + s(arr, i + 1, j), arr[j] + s(arr, i, j - 1));
    }

    public static int s(int[] arr, int i, int j) {//后拿的
        //如果i == j，即arr[i...j]上只有一张纸牌，作为后拿的人必然什么也得不到，所以返回0；
        if (i == j) {
            return 0;
        }
        //因为对手会拿走最好的，所以当前玩家只能拿最差的
        return Math.min(f(arr, i + 1, j), f(arr, i, j - 1));
    }

 

 

改动态规划，两张表。分析递归函数，i和j的变化范围（index变化范围）。

i肯定不会大于j（下半区域直接不用填），先看目标位置（打星星的地方），然后填上固定的值，i==j是对角线，填上对应的值。

 

 

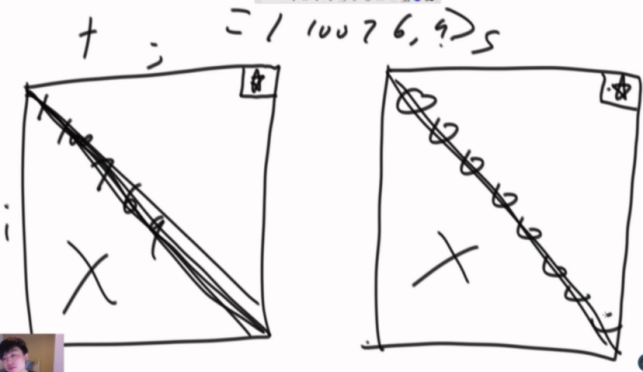
然后看普遍位置是怎么依赖的。

F（i，j）依赖与他相对称的S（i，j）的

s(arr, i + 1, j), s(arr, i, j - 1);

同理S的点也依赖F的同样位置。

 

 

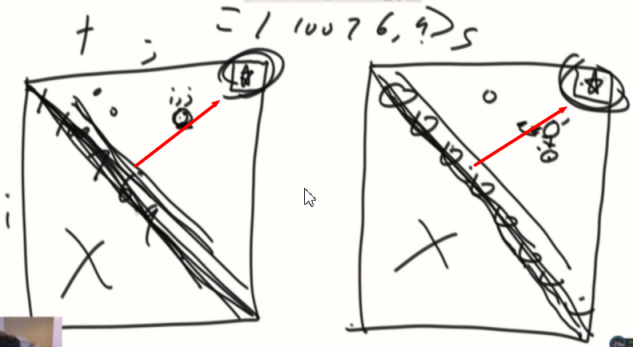
通过对角线一行行直到把终止位置（那个小星星）推出来。

    public static int win2(int[] arr) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        int[][] f = new int[arr.length][arr.length];
        int[][] s = new int[arr.length][arr.length];
        //一边设置对角线，一边计算值，对角线慢慢向上走
        for (int j = 0; j < arr.length; j++) {
            f[j][j] = arr[j];
            //设计的很好，以列为首要遍历条件，再逐行向下计算
            for (int i = j - 1; i >= 0; i--) {
                f[i][j] = Math.max(arr[i] + s[i + 1][j], arr[j] + s[i][j - 1]);
                s[i][j] = Math.min(f[i + 1][j], f[i][j - 1]);
            }
        }
        return Math.max(f[0][arr.length - 1], s[0][arr.length - 1]);
    }

    public static void main(String[] args) {
        int[] arr = { 1, 9, 1 };
        System.out.println(win2(arr));
        System.out.println(win1(arr));

    }

 

 

 

2017年阿里的题目：

一个长度为N的路，1~N

一个机器人在M位置，他可以走P步，如果在1只能走右，在N只能走左，请问机器人走P步后他停在K位置上的走法有多少种。

 

 

 

    public static int walk(int N, int curPosition, int remainSteps, int K) {
        if (N < 1 || curPosition < 1 || curPosition > N || remainSteps < 0 || K > N) {
            return 0;
        }

        if (remainSteps == 0) {
            return curPosition == K ? 1 : 0;
        }
        int count = 0;
        if (curPosition == 1) {
            count = walk(N, curPosition + 1, remainSteps - 1, K);
        } else if (curPosition == N) {
            count = walk(N, curPosition - 1, remainSteps - 1, K);
        } else {
            count = walk(N, curPosition + 1, remainSteps - 1, K) + walk(N, curPosition - 1, remainSteps - 1, K);
        }
        return count;
    }

 

 

改动态规划，可变参数是M（机器人位置）和P（可以走的步数）

 

 

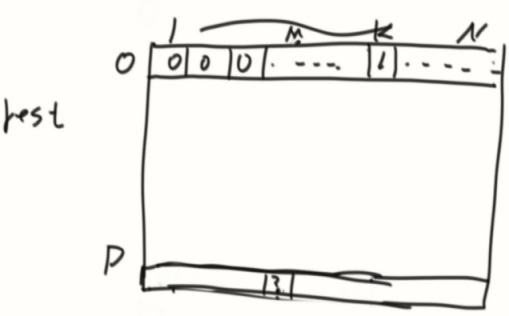
最后需要获取的位置是（M,P）

普遍依赖，

 

curPosition + 1, remainSteps - 1
curPosition - 1, remainSteps - 1

 

 

杨辉三角形

 

 

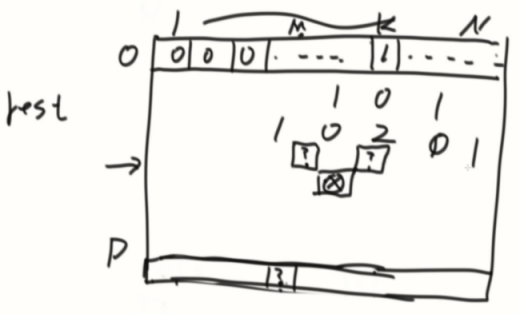
计算到最后一排，看落到M上的数是几就返回几。

会撞墙的杨辉三角形（指的是在1和N的情况）

 

    public static int dpWalk(int N, int curPosition, int remainSteps, int K) {
        int[][] dp = new int[remainSteps + 1][N + 1];
        dp[0][K] = 1;

        for (int i = 1; i <= remainSteps; i++) {
            for (int j = 1; j <= N; j++) {
                dp[i][j] += j - 1 < 1 ? 0 : dp[i - 1][j - 1];
                dp[i][j] += j + 1 > N ? 0 : dp[i - 1][j + 1];
            }
        }

        return dp[remainSteps][curPosition];
    }

    public static void main(String[] args) {
        System.out.println(walk(5, 3, 0, 3));
        System.out.println(walk(5, 3, 2, 3));
        System.out.println(dpWalk(5, 3, 0, 3));
        System.out.println(dpWalk(5, 3, 2, 3));
    }

 

只要你会试，什么都无所谓。

 

首先是递归试法，发现有多余的计算浪费，衍生出记忆化搜索，加上空间感后，用空间换了时间，即是动态规划。