算法进阶面试题05——树形dp解决步骤、返回最大搜索二叉子树的大小、二叉树最远两节点的距离、晚会最大活跃度、手撕缓存结构LRU

接着第四课的内容，加入部分第五课的内容，主要介绍树形dp和LRU

 

第一题：

给定一棵二叉树的头节点head，请返回最大搜索二叉子树的大小

 

二叉树的套路

统一处理逻辑：假设以每个节点为头的这棵树，他的最大搜索二叉子树是什么。答案一定在其中

 

第一步，列出可能性（最难部分）

1、可能来自左子树上的某课子树

2、可能来自右子树上的某课子树

3、整颗都是（左右子树都是搜索二叉树并且左子树最大小于该节点，右子树最小大于该节点）

 

 

 

第二步，收集信息：

1、左树最大搜索子树大小

2、右树最大搜索子树大小

3、左树最大二叉搜索子树的头部（通过查看这个头部是否等于节点的左孩子，来判断整个左子树是否都是二叉搜索树）

4、右树最大二叉搜索子树的头部

5、左树最大值

6、右树最小值

 

 

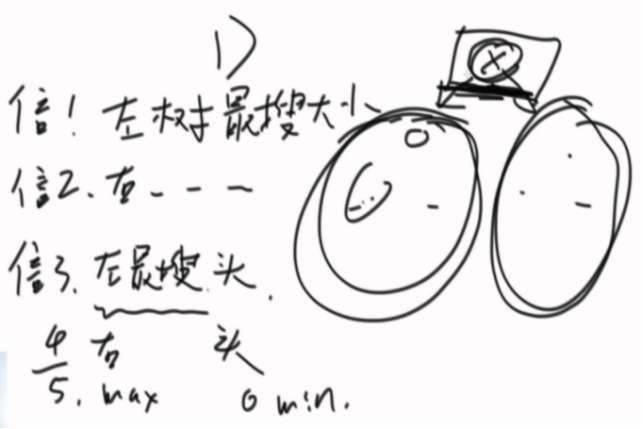
化简为一个信息体：

1、左/右搜大小

2、左/右搜头

3、左max

4、右min

 

不管左树还是右树都存储

1、最大搜索子树大小

2、最大搜索子树的头部

3、这棵树上的最大值和最小值

 

如果不理解可以看引子题（很简单的）

一棵树中找最大最小

 

 

 

 

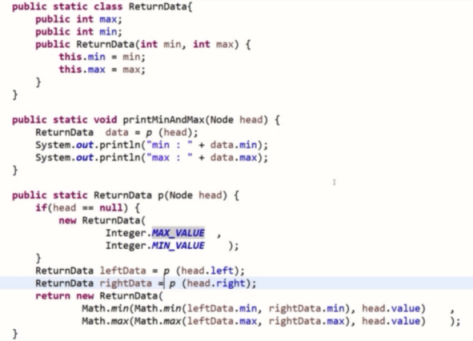
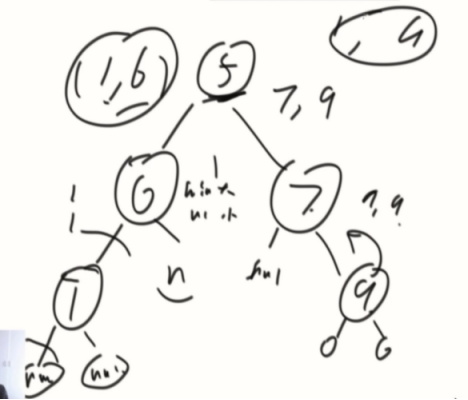
第三步，改递归（比较复杂）

先假设左和右都给我这样的信息了，然后怎么利用左边和右边的信息，组出来我该返回的信息。最后baseKey填什么，搞定！

 

public class Code_04_BiggestSubBSTInTree {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    public static Node biggestSubBST(Node head) {
        int[] record = new int[3]; // 0->size, 1->min, 2->max
        return posOrder(head, record);
    }
    
    public static class ReturnType{
        public int size;
        public Node head;
        public int min;
        public int max;
        
        public ReturnType(int a, Node b,int c,int d) {
            this.size =a;
            this.head = b;
            this.min = c;
            this.max = d;
        }
    }
    
    public static ReturnType process(Node head) {
        if(head == null) {
            //设置系统最大最小为了不干扰判断最大最小的决策
            return new ReturnType(0,null,Integer.MAX_VALUE, Integer.MIN_VALUE);
        }
        Node left = head.left;
        ReturnType leftSubTressInfo = process(left);//当成一个黑盒
        Node right = head.right;
        ReturnType rightSubTressInfo = process(right);
        
        int includeItSelf = 0;
        if(leftSubTressInfo.head == left 
                &&rightSubTressInfo.head == right
                && head.value > leftSubTressInfo.max
                && head.value < rightSubTressInfo.min
                ) {
            includeItSelf = leftSubTressInfo.size + 1 + rightSubTressInfo.size;
        }
        int p1 = leftSubTressInfo.size;
        int p2 = rightSubTressInfo.size;
        //解黑盒的过程
        int maxSize = Math.max(Math.max(p1, p2), includeItSelf);

        Node maxHead = p1 > p2 ? leftSubTressInfo.head : rightSubTressInfo.head;
        if(maxSize == includeItSelf) {
            maxHead = head;
        }
        
        return new ReturnType(maxSize,
                maxHead, 
                Math.min(Math.min(leftSubTressInfo.min,rightSubTressInfo.min),head.value),
                Math.max(Math.max(leftSubTressInfo.max,rightSubTressInfo.max),head.value));    
    }

    //数组实现版本
    public static Node posOrder(Node head, int[] record) {
        if (head == null) {
            record[0] = 0;
            record[1] = Integer.MAX_VALUE;
            record[2] = Integer.MIN_VALUE;
            return null;
        }
        int value = head.value;
        Node left = head.left;
        Node right = head.right;
        Node lBST = posOrder(left, record);
        int lSize = record[0];
        int lMin = record[1];
        int lMax = record[2];
        Node rBST = posOrder(right, record);
        int rSize = record[0];
        int rMin = record[1];
        int rMax = record[2];
        record[1] = Math.min(rMin, Math.min(lMin, value)); // lmin, value, rmin -> min 
        record[2] =  Math.max(lMax, Math.max(rMax, value)); // lmax, value, rmax -> max
        if (left == lBST && right == rBST && lMax < value && value < rMin) {
            record[0] = lSize + rSize + 1;
            return head;
        }
        record[0] = Math.max(lSize, rSize);
        return lSize > rSize ? lBST : rBST;
    }

    // for test -- print tree
    public static void printTree(Node head) {
        System.out.println("Binary Tree:");
        printInOrder(head, 0, "H", 17);
        System.out.println();
    }

    public static void printInOrder(Node head, int height, String to, int len) {
        if (head == null) {
            return;
        }
        printInOrder(head.right, height + 1, "v", len);
        String val = to + head.value + to;
        int lenM = val.length();
        int lenL = (len - lenM) / 2;
        int lenR = len - lenM - lenL;
        val = getSpace(lenL) + val + getSpace(lenR);
        System.out.println(getSpace(height * len) + val);
        printInOrder(head.left, height + 1, "^", len);
    }

    public static String getSpace(int num) {
        String space = " ";
        StringBuffer buf = new StringBuffer("");
        for (int i = 0; i < num; i++) {
            buf.append(space);
        }
        return buf.toString();
    }

    public static void main(String[] args) {

        Node head = new Node(6);
        head.left = new Node(1);
        head.left.left = new Node(0);
        head.left.right = new Node(3);
        head.right = new Node(12);
        head.right.left = new Node(10);
        head.right.left.left = new Node(4);
        head.right.left.left.left = new Node(2);
        head.right.left.left.right = new Node(5);
        head.right.left.right = new Node(14);
        head.right.left.right.left = new Node(11);
        head.right.left.right.right = new Node(15);
        head.right.right = new Node(13);
        head.right.right.left = new Node(20);
        head.right.right.right = new Node(16);

        printTree(head);
        Node bst = biggestSubBST(head);
        printTree(bst);

    }

}

 

 

第二题，继续套路：

二叉树中，一个节点可以往上走和往下走，那么从节点A总能走到节点B。

节点A走到节点B的距离为：A走到B最短路径上的节点个数。

求一棵二叉树上的最远距离

 

 

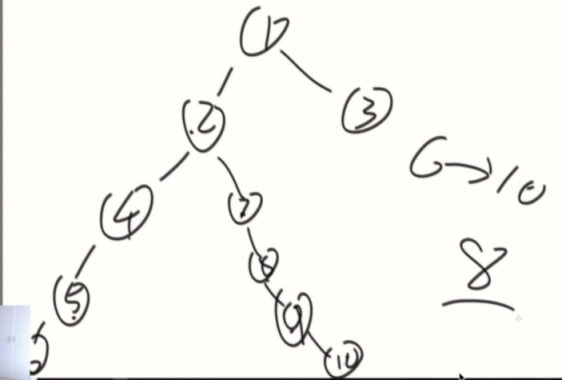
列可能性：

1、来自左子树最长距离

2、来自右子树最长距离

3、经过X的情况下的最远距离，左树最深+右树最深+1

 

 

  

 

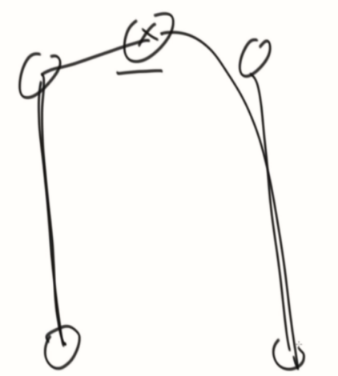
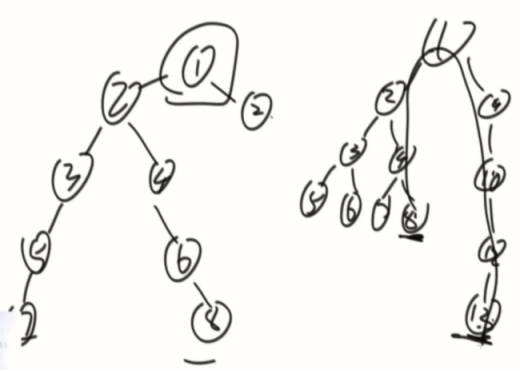
收集信息：

1、最长距离

2、深度

 

 

public class Code_03_MaxDistanceInTree {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    public static int maxDistance(Node head) {
        int[] record = new int[1];
        return posOrder(head, record);
    }
    
    public static class ReturnType{
        public int maxDistance;
        public int h;
        
        public ReturnType(int m, int h) {
            this.maxDistance = m;
            this.h = h;
        }
    }
    
    public static ReturnType process(Node head) {
        if(head == null) {
            return new ReturnType(0,0);
        }
        ReturnType leftReturnType = process(head.left);
        ReturnType rightReturnType = process(head.right);
        int includeHeadDistance = leftReturnType.h + 1 + rightReturnType.h;
        int p1 = leftReturnType.maxDistance;
        int p2 = rightReturnType.maxDistance;
        int resultDistance = Math.max(Math.max(p1, p2), includeHeadDistance);
        int hitSelf  = Math.max(leftReturnType.h, leftReturnType.h) + 1;
        return new ReturnType(resultDistance, hitSelf);
    }

    public static int posOrder(Node head, int[] record) {
        if (head == null) {
            record[0] = 0;
            return 0;
        }
        int lMax = posOrder(head.left, record);
        int maxFromLeft = record[0];
        int rMax = posOrder(head.right, record);
        int maxFromRight = record[0];
        int curNodeMax = maxFromLeft + maxFromRight + 1;
        record[0] = Math.max(maxFromLeft, maxFromRight) + 1;
        return Math.max(Math.max(lMax, rMax), curNodeMax);
    }

    public static void main(String[] args) {
        Node head1 = new Node(1);
        head1.left = new Node(2);
        head1.right = new Node(3);
        head1.left.left = new Node(4);
        head1.left.right = new Node(5);
        head1.right.left = new Node(6);
        head1.right.right = new Node(7);
        head1.left.left.left = new Node(8);
        head1.right.left.right = new Node(9);
        System.out.println(maxDistance(head1));

        Node head2 = new Node(1);
        head2.left = new Node(2);
        head2.right = new Node(3);
        head2.right.left = new Node(4);
        head2.right.right = new Node(5);
        head2.right.left.left = new Node(6);
        head2.right.right.right = new Node(7);
        head2.right.left.left.left = new Node(8);
        head2.right.right.right.right = new Node(9);
        System.out.println(maxDistance(head2));

    }

}

 

扩充：如果是计算两个固定节点a~b的距离，需要找出他们的最近公共祖先，然后计算a~公共祖先+b~公共祖先。

 

 

第三题

一个公司的上下节关系是一棵多叉树，这个公司要举办晚会，你作为组织者已经摸清了大家的心理：一个员工的直接上级如果到场，这个员工肯定不会来。每个员工都有一个活跃度的值，决定谁来你会给这个员工发邀请函，怎么让舞会的气氛最活跃？返回最大的活跃值。

举例：

给定一个矩阵来表述这种关系

matrix =

{

1,6

1,5

1,4

}

这个矩阵的含义是：

matrix[0] = {1 , 6}，表示0这个员工的直接上级为1,0这个员工自己的活跃度为6

matrix[1] = {1 , 5}，表示1这个员工的直接上级为1（他自己是这个公司的最大boss）,1这个员工自己的活跃度为5

matrix[2] = {1 , 4}，表示2这个员工的直接上级为1,2这个员工自己的活跃度为4

为了让晚会活跃度最大，应该让1不来，0和2来。最后返回活跃度为10

 

 

 

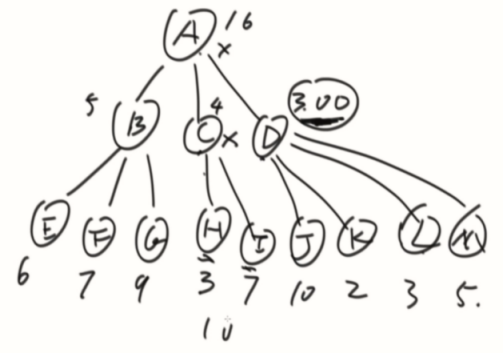
可能性

1、X来，活跃度就是x活跃度+x1不来+x2不来+x3不来的总和。

2、X不来，活跃度就是x1/x2/x3来和不来中选最大的总和。

 

 

 

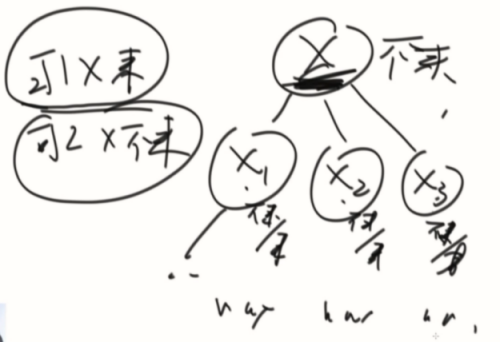
收集信息：

1、一棵树在头结点来的活跃度

2、一棵树在头结点不来的活跃度

 

 

public class Code_04_MaxHappy {

    public static class Node{
        public int happy;
        public ArrayList<Node> nexts;

        public Node(int happy){
            this.happy  = happy;
            nexts = new ArrayList<Node>();
        }
    }

    public static class ReturnData{
        public int comeHappy;
        public int notComeHappy;

        public ReturnData(int c,int nc){
            comeHappy = c;
            notComeHappy = nc;
        }
    }

    public static ReturnData process(Node head){
        int comeHappy = head.happy;
        int notComeHappy = 0;

        for (int i = 0;i!=head.nexts.size();i++){
            ReturnData data = process(head.nexts.get(i));
            comeHappy += data.notComeHappy;
            notComeHappy += Math.max(data.notComeHappy,data.comeHappy);
        }
        return new ReturnData(comeHappy,notComeHappy);
    }

    public static int calcMaxHappy(Node head){
        ReturnData data = process(head);
        return Math.max(data.comeHappy, data.notComeHappy);
    }

    //下面是用数组结构去求
    public static int maxHappy(int[][] matrix) {
        int[][] dp = new int[matrix.length][2];
        boolean[] visited = new boolean[matrix.length];
        int root = 0;
        for (int i = 0; i < matrix.length; i++) {
            if (i == matrix[i][0]) {
                root = i;
            }
        }
        process(matrix, dp, visited, root);
        return Math.max(dp[root][0], dp[root][1]);
    }

    public static void process(int[][] matrix, int[][] dp, boolean[] visited, int root) {
        visited[root] = true;
        dp[root][1] = matrix[root][1];
        for (int i = 0; i < matrix.length; i++) {
            if (matrix[i][0] == root && !visited[i]) {
                process(matrix, dp, visited, i);
                dp[root][1] += dp[i][0];
                dp[root][0] += Math.max(dp[i][1], dp[i][0]);
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 8 }, { 1, 9 }, { 1, 10 } };
        System.out.println(maxHappy(matrix));
    }
}

 

 

上述所有题目都叫树形dp。（列可能性）

思路：小树计算完，再算父亲树。

 

summary（总结）

1、分析可能性（先计算小树，再计算大树）

2、列信息全集，定下返回值结构。

3、编写代码的时候，默认每颗子树都给你这样的信息，然后看拿到这些子树信息后怎么加工出父的信息。

4、basekey要单独考虑一下，作为最简单的情况，要给父返回啥，不至于让他干扰。

 

第四题：（基础班讲过）

判断一棵树是否是平衡二叉树

 

public class c04_04IsBalancedTree {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    public static class ReturnData{
        public boolean isBalance;
        public int level;

        public ReturnData(boolean isBalance, int level) {
            this.isBalance = isBalance;
            this.level = level;
        }
    }

    public static ReturnData process(Node head){
        if(head == null){
            return new ReturnData(true,0);
        }
        //如果左子树或者右子树返回了他们不是平衡的，那总体也不会是平衡的
        ReturnData lRData = process(head.left);
        if(!lRData.isBalance){
            return new ReturnData(true,0);
        }
        ReturnData rRData = process(head.right);
        if(!rRData.isBalance){
            return new ReturnData(true,0);
        }
        if(Math.abs(lRData.level - rRData.level) > 1){
            return new ReturnData(true,0);
        }
        return new ReturnData(true,Math.max(lRData.level,rRData.level)+1);
    }

    public static void main(String[] args) {
        Node head = new Node(1);
        head.left = new Node(2);
        head.right = new Node(3);
        head.left.left = new Node(4);
        head.left.right = new Node(5);
        head.right.left = new Node(6);
        head.right.right = new Node(7);

        System.out.println(process(head).isBalance);
    }

}

 

第五题：

数据结构设计题（LeetCode中等难度）难在code上

设计可以变更的缓存结构（LRU）（经常使用的留下）

【题目】

设计一种缓存结构，该结构在构造时确定大小，假设大小为K，并有两个功能：

set(key,value)：将记录(key,value)插入该结构。

get(key)：返回key对应的value值。

【要求】

1．set和get方法的时间复杂度为O(1)。

2．某个key的set或get操作一旦发生，认为这个key的记录成了最经常使用的。

3．当缓存的大小超过K时，移除最不经常使用的记录，即set或get最久远的。

【举例】

假设缓存结构的实例是cache，大小为3，并依次发生如下行为：

1．cache.set("A",1)。最经常使用的记录为("A",1)。

2．cache.set("B",2)。最经常使用的记录为("B",2)，("A",1)变为最不经常的。

3．cache.set("C",3)。最经常使用的记录为("C",2)，("A",1)还是最不经常的。

4．cache.get("A")。最经常使用的记录为("A",1)，("B",2)变为最不经常的。

5．cache.set("D",4)。大小超过了3，所以移除此时最不经常使用的记录("B",2)，加入记录 ("D",4)，并且为最经常使用的记录，然后("C",2)变为最不经常使用的记录

 

 

 

思路：hash表（key，Node<key,value>内存地址）+定制的双向链表（尾加头出）

 

 

加入的时候先把节点从环境分离，挂到最后，再重连其他节点。

有一个size记录大小，在删的时候可以通过head指针把优先级最低的删除，再根据key到hash里面寻找并彻底删除。

 

 

public class Code_02_LRU {

    public static class Node<K,V> {
        public K key;
        public V value;
        public Node<K,V> last;
        public Node<K,V> next;

        public Node(K key,V value) {
            this.key = key;
            this.value = value;
        }
    }
    //定制的双向链表
    public static class NodeDoubleLinkedList<K,V> {
        private Node<K,V> head;
        private Node<K,V> tail;

        public NodeDoubleLinkedList() {
            this.head = null;
            this.tail = null;
        }

        public void addNode(Node<K,V> newNode) {
            if (newNode == null) {
                return;
            }
            if (this.head == null) {
                this.head = newNode;
                this.tail = newNode;
            } else {//最新的添加到尾部
                this.tail.next = newNode;
                newNode.last = this.tail;//新节点的前一个是之前的尾部
                this.tail = newNode;
            }
        }
        //操作节点后把结点调整在尾部
        public void moveNodeToTail(Node<K,V> node) {
            if (this.tail == node) {
                return;
            }
            //先把节点从环境分离
            if (this.head == node) {
                this.head = node.next;
                this.head.last = null;
            } else {//中间的普遍节点
                node.last.next = node.next;
                node.next.last = node.last;
            }
            node.last = this.tail;
            node.next = null;
            this.tail.next = node;
            this.tail = node;
        }
        //容量满了删除最不经常操作的数
        public Node<K,V> removeHead() {
            if (this.head == null) {
                return null;
            }
            Node<K,V> res = this.head;
            if (this.head == this.tail) {//只有一个节点
                this.head = null;
                this.tail = null;
            } else {
                this.head = res.next;
                res.next = null;
                this.head.last = null;
            }
            return res;
        }

    }

    public static class MyCache<K, V> {
        //通过key可以找到Node
        private HashMap<K, Node<K,V>> keyNodeMap;
        private NodeDoubleLinkedList<K,V> nodeList;
        private int capacity;

        public MyCache(int capacity) {
            if (capacity < 1) {
                throw new RuntimeException("should be more than 0.");
            }
            this.keyNodeMap = new HashMap<K, Node<K,V>>();
            this.nodeList = new NodeDoubleLinkedList<K,V>();
            this.capacity = capacity;
        }

        public V get(K key) {
            if (this.keyNodeMap.containsKey(key)) {
                Node<K,V> res = this.keyNodeMap.get(key);
                this.nodeList.moveNodeToTail(res);
                return res.value;
            }
            return null;
        }

        public void set(K key, V value) {
            if (this.keyNodeMap.containsKey(key)) {
                Node<K,V> node = this.keyNodeMap.get(key);
                node.value = value;
                this.nodeList.moveNodeToTail(node);
            } else {//没有就新增
                Node<K,V> newNode = new Node<K,V>(key,value);
                this.keyNodeMap.put(key, newNode);
                this.nodeList.addNode(newNode);
                if (this.keyNodeMap.size() == this.capacity + 1) {
                    this.removeMostUnusedCache();
                }
            }
        }

        private void removeMostUnusedCache() {
            Node<K,V> removeNode = this.nodeList.removeHead();//取出优先级最低的
            K removeKey = removeNode.key;
            this.keyNodeMap.remove(removeKey);
        }

    }

    public static void main(String[] args) {
        MyCache<String, Integer> testCache = new MyCache<String, Integer>(3);
        testCache.set("A", 1);
        testCache.set("B", 2);
        testCache.set("C", 3);
        System.out.println(testCache.get("B"));
        System.out.println(testCache.get("A"));
        testCache.set("D", 4);
        System.out.println(testCache.get("D"));
        System.out.println(testCache.get("C"));

    }

}

 

 

就是有限的几个结构组成出来。（链表、hash）

 

 

 

自定义的Node，Map会存内存地址（8字节）。

 

回去看一下LFU。