1. LogPolar
LogPolar是将笛卡尔坐标到对数极坐标的变换.即:将 (x,y) 映射到 (log(ρ),θ)
2. 笛卡尔空间&笛卡尔坐标
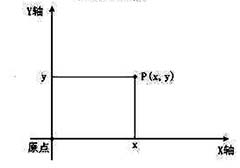
笛卡尔坐标系(Cartesiancoordinates)就是直角坐标系和斜角坐标系的统称.本文中用到的是平面直角坐标系.
3. 极坐标
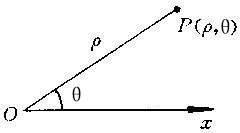
在平面上取一定点o,称为极点,由o出发的一条射线ox,称为极轴。再取定一个长度单位,通常规定角度取逆时针方向为正。这样,平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ来确定,有序数对(ρ,θ)就称为P点的极坐标,记为P(ρ,θ);ρ称为P点的极径,θ称为P点的极角。
4. 笛卡尔坐标到极坐标变换
在OpenCV中使用函数CartToPolar()实现.
5. 自然常数e(欧拉数)
自然常数e(约为2.71828)其是公式为
6. 对数定义
若a^n=b(a>0且a≠1) 则n=logab。其中,a叫做“底数”,b叫做“真数”,n叫做“以a为底的b的对数”。零和负数没有对数。在数学中,当不写底数时,一般默认以10为底数。在c语言函数中,log()是以e为底的对数,log10()是以10为底的对数。这里讨论的是以e为底的对数.
log(20) => e^n=20 => n=2.99 (自然对数)
exp(2.99)=> e^2.99 => 20 (自然指数)
7. 具体应用
指数和对数的转换,可以理解为一种映射,以自然对数为例,x大幅变化,y将小幅变化,因此可将大幅变化投射到相对小的区域,从而简化运算.
在图像处理中的应用,LogPolar将笛卡尔坐标系映射到对数极坐标系后,再做对数变换,原理是:人眼的视觉中心有很高的分辨率,但是随着离心距离的增大,分辨率不断降低。于是达到类似聚焦的效果.即视焦点区域清晰,外围逐渐模糊.LogPolar实现了类似变换,通过取对数操作弱化了焦点以外的区域,简化图像,以便进一步处理.



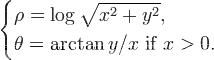
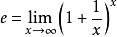



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具