1. 用途
根据一些已知的量来预测未知的量。常用于运动预测。
2. 定义
卡尔曼滤波(Kalmanfiltering)一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。
由于观测数据中包括系统中的噪声和干扰的影响,最优估计也可看作是滤波过程,因此叫作卡尔曼滤波。
3. 原理分析
1) 第一部分:预测值与误差
a) 假设你和我两个人每天给同一头猪测体重,但两个称都不准。你测x1斤,正负误差在σ1斤左右(假设预测成高斯分布,标准差反映了测量值好坏程度的不确定性),我测x2斤,正负误差在σ2斤左右。结合两个人的预测,简单计算猪的体重是x1和x2的平均值。
b) 假如我的称更准,即误差更小,σ2<σ1,结合两个人的测量,应该以我为主,因此根据误差加权组合。
(通过概率函数导数的最大值推出上述公式,不在此详述)
由公式可知:如果你的不确定性σ1越大,我的测量值x2在新均值中占的比例越大(权值更大)。
c) 后来你走了,用上一次的加权平均(x1^,σ1^)替代你的测量,我的测量值仍是(x2, σ2)(此后我们把加权平均的结果称为预测值)。同样采取加权平均的算法,算出本次预测值(x2^,σ2^),这是一个迭代的过程。通过化简得到以下公式:
请注意,现在公式中的1,2不再代表你和我,而代表时间点,带^的为预测值,不带^的为测量值。也就是说新的预测值(x2^, σ2^)由前一个预测值(x1^, σ1^)和本次测量值(x2, σ2)求得。为简化公式引入更新率K,即卡尔曼增益(KalmanGain)。将公式简化为以下形式:
从简化之后的公式可知,K是由误差算出的,K用于预测新的x和误差σ。
由公式可知:前次预测的不确定性σ1^越大,K越大,我的预测x2越重要。
d) 综上,我们已经看到了最简单(单值且预测与测量的值相同)情况下的测量值与前次的预测值,是如何预测之后的值x与误差σ的,下面我们将它推广到更复杂的情况。
2) 第二部分:如何预测
a) 已知当前点的状态,如何预测下一时间点的状态。
首先要考虑猪前一天的状态Xk-1,猪的成长变化,正常情况下每天长两斤(F);它每跑步一圈减半斤(B),某天可能跑(uk)圈;还要考虑天气等不可控外力(wk)。因此,猪从第k天的体重Xk由下式预测:
总之,想预测他的未来,先要知道它之前的状态,自身成长系数,培养教育,对培养教育的反应,以及不可控的机遇,人也是一样哈。
b) 后来,称猪的称丢了,现在只有一个尺子,我们通过量猪腰围Zk。然后乘以系数Hk,来估计猪的体重,同时还要考虑尺子的测量误差vk。
此时,测量值和预测值已经不是同一属性了。
c) 再后来,发现只量腰围还不够,还需要量身高,也就是说Zk不再是单一变量,而是一组向量,此时H就变成了一个矩阵,用于转换测量维度z和预测维度x。
同理我们可能预测更多的x状态,比如猪的大小,体脂;另外影响猪长肉的外在因素也不只跑圈,可能还有喂食多少。此时上述公式就从一维扩展到了N维。公式中的F,B,H,w,v是一维到多维矩阵。x ,u, z是一维到多维向量。
但本质没变,都是通过测量值和之前预测值的误差,求卡尔曼增益,然后进行下一次预测。
d) 综上,即是卡尔曼方程
xk是k时刻的系统状态,是一个n维状态向量。
F是传递矩阵,它是一个nxn的矩阵,描述的是xk-1与xk间变化的关系。它是变化的内因。
uk是k时刻的控制输入,它是变化的外因,它由c维向量组成。
B是控制矩阵,它是一个nxc的矩阵,它是变化的外因。
wk是过程噪声,它是具有高斯分布的随机事件,nxn的协方差矩阵。
zk是k时刻的测量值,是一个m维状态向量。
Hk是测量矩阵,它是mxn的矩阵。描述的是Xk与Zk间的关系。
Vk是测量误差,它是具有高斯分布的随机事件,mxm的协方差矩阵。
3) 第三部分:复杂的多维数据代入加权平均算法
a) 至此我们看到了x和x^是如何变化的,下面来考虑σ以及K。
Xk^是对Xk的预测,对应第一部分中的x。
Pk^是误差协方差矩阵,对应第一部分中的误差σ。
Qk-1是过程噪声。
Kk是卡尔曼增益。
Rk是测试噪声。
4. 相关程序
在opencv中使用kalman预测的效果,可通过例程opencv/samples/cpp/kalman.cpp调用。
程序基本分为三个部分:初始化,预测,更新。在初始化时,我们先指定传递矩阵,控制矩阵,测量矩阵,噪声矩阵;迭代过程中通过测量值更新;预测新的状态。
Kalman的具体实现,请参考程序opencv/modules/video/src/kalman.cpp,下面是其预测和更新部分(对应第三部分的公式):
const Mat& KalmanFilter::predict(const Mat& control)
{
CV_INSTRUMENT_REGION()
// update the state: x'(k) = A*x(k),通过xk-1^预测xk^
statePre = transitionMatrix*statePost;
if( !control.empty() )
// x'(k) = x'(k) + B*u(k),计算外因影响:控制矩阵
statePre += controlMatrix*control;
// update error covariance matrices: temp1 = A*P(k)
temp1 = transitionMatrix*errorCovPost;
// P'(k) = temp1*At + Q,更新误差Pk^
gemm(temp1, transitionMatrix, 1, processNoiseCov, 1, errorCovPre, GEMM_2_T);
// handle the case when there will be measurement before the next predict.
statePre.copyTo(statePost);
errorCovPre.copyTo(errorCovPost);
// 至此可以看到,预测后得到了xk^,以及误差Pk^
return statePre;
}
const Mat& KalmanFilter::correct(const Mat& measurement)
{
CV_INSTRUMENT_REGION()
// temp2 = H*P'(k)
temp2 = measurementMatrix * errorCovPre;
// temp3 = temp2*Ht + R
gemm(temp2, measurementMatrix, 1, measurementNoiseCov, 1, temp3, GEMM_2_T);
// temp4 = inv(temp3)*temp2 = Kt(k)
solve(temp3, temp2, temp4, DECOMP_SVD);
// K(k),卡尔曼增益K
gain = temp4.t();
// temp5 = z(k) - H*x'(k),见第一部分中的x2-x1^
temp5 = measurement - measurementMatrix*statePre;
// x(k) = x'(k) + K(k)*temp5,计算xk-1^
statePost = statePre + gain*temp5;
// P(k) = P'(k) - K(k)*temp2,计算误差
errorCovPost = errorCovPre - gain*temp2;
return statePost;
}






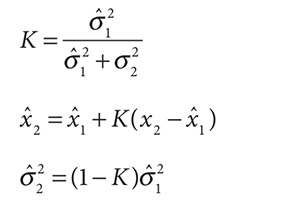
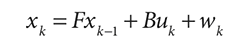
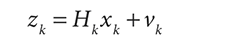
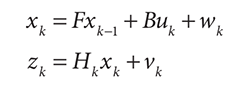
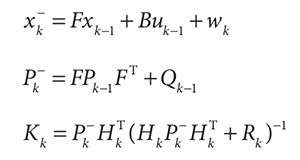


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具