K-Shape 高效且准确的时间序列的聚类方法
基本信息
- 论文题目：k-Shape: Efficient and Accurate Clustering of Time Series
- 论文地址：https://dl.acm.org/doi/10.1145/2949741.2949758
- 相关源码：https://github.com/tslearn-team/tslearn/
- 用法示例：https://tslearn.readthedocs.io/en/stable/auto_examples/clustering/plot_kshape.html#sphx-glr-auto-examples-clustering-plot-kshape-py
这是一篇发表于2015年SIGMODE数据管理国际顶会的论文，它主要针对时序数据的聚类问题，提出了K-Shape方法。与以往的方法相比，它优化了距离计算方法，质心计算方法，还引入了提取频域特征方法，以提升效率。
作者认为它是一种独立于领域、高精度、高效率的时间序列聚类方法。
我觉得相对于传统方法，它聚类效果更好；相对于DTW类方法，效果稍差，但速度快很多。毕竟从原理来看，K-Shape只考虑了纵向拉伸和横向平移，而DTW还考虑了横向拉伸。
算法
K-Shape原理和K-means相似，不同在于它改进了距离计算方法，并优化了质心计算方法。一方面支持振幅缩放和平移不变性，另一方面计算效率也比较高，并且不用手动设置参数，便于扩展到更多领域。
距离算法
距离算法用于计算两组时序数据的差异，其中的核心问题是如何处理时序数据的形变，论文中的图-1 展示的心电图数据被分为A/B两类：
其中A类的特点是：上升->下降->上升，而B类的特点是：下降->上升。图-1 的右下图展示了理想的建模效果，它识别到了相同的模式，而忽略了幅度和相位的差异。人们也更倾向使用这种方法计算距离，很多时候甚至认为距离计算方法比聚类方法更加重要。一般来说，支持振幅缩放和平移不变性的方法，计算成本较高，难以对大数据量建模。
其它距离计算方法
K-Shape之前的主流距离算法如下：
- ED: 欧几里得距离，最简单效率也最高，直接计算两个时间序列的距离，不考虑横向纵向缩放平移等问题。
- DTW: 动态时间规整，考虑缩放和平移的情况，可用于比较长短不一的序列，效果好但资源占用高。
- cDTW: DTW的限制版本，它将变化限制在一定的“带”之内，有效地提高了DTW的效率和准确率。
互相关方法
K-Shape用互相关方法计算两个时间序列的距离。假设有X和Y两个时间序列，序列长度均为m。为实现平移不变性，Y不变，一步一步划动X，并计算每一步X与Y的差异。
如上图所示：假设绿色区域为Y，白色区域为划动的X，每一行s（step)向前划动一步，序列长度为m=4，s∈(-3,3)共7种取值，w是所有移动的可能性2m-1=7次，w-m=s=k，也就是下面公式中的对齐位置（对齐逻辑贯穿整个算法）。
定义互相关系数CC：
利用R来计算x和y在每一步的相似度，在对的上(在X,Y中都存在)的位置计算点积，最终R是有效区域的点积之和（对每个对上的小块加和）。可以说，R越大两个序列越相似。
由于对比的每个子序列振幅不同，块数也不同，所以在对比时需要进行归一化，归一化方法有三种， 第三种使用了互相关方法，效果最好。
归一化效果如下图所示：
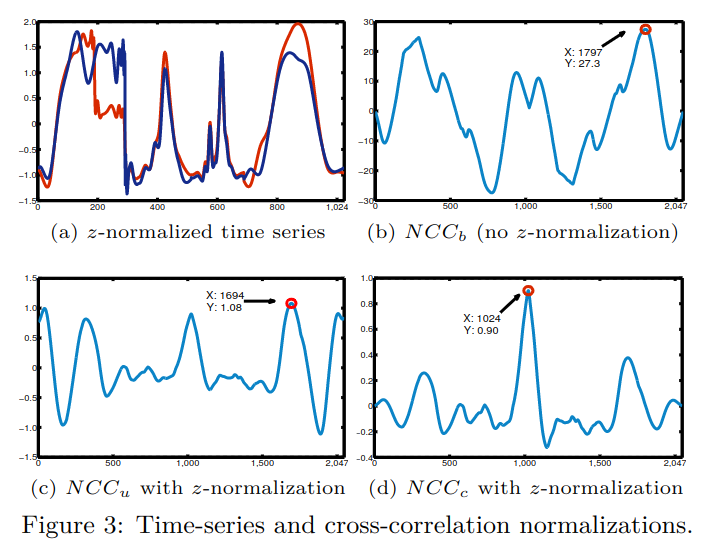
其中图(a)使用z-normalization只做了对振幅的归一化，没有平移，可见在上述情况下，不平移（正对上）时对齐效果最好。从(b)(c)(d)可以看到：(d)图使用第三种方法，在最中间的点上相似度值最大（s=0时），即正对上的时候，其相似度最大，这与(a)呈现出的效果一致。而(b)(c)都认为最相似的情况出现在右侧，这明显不太对。
文中定义了基于形态的距离SBD（Shape-based distance），块重叠越多形状越像CC越大，对比所有可能位置的相似度值，取最相似的max(CC)，然后用1-max(CC)得到SBD，也就是说形状越相似，距离SBD越小，归一化后的NCC值在[-1,1]之间，因此，SBD值在[0,2]之间。
可以看到，用以上方法时间在序列较长时复杂度比较高，当序列较长时，计算量也会很大，为解决这一问题，作者提出使用傅里叶变换将序列由时域转到频域再比较，以节约计算量。
计算质心
定义了距离之后，还需要根据距离逻辑来调整质心算法。
从图-4 可以看到：时序数据的质心也是一条时序变化线，图中的蓝色线使用均值方法（计算每个点的均值）来计算质心；由于错位，波峰和波谷被拉成了直线，因此不能正确地表达形状趋势。
K-Shape使用基于SBD的方式计算质心。
该公式的目标是寻找μk*，使质心μk与该簇Pk中各条序列xi的相似度NCC最大。
算法一：先使用SBD() 函数计算dist和y'，dist是时序x,y之间的距离，y'是y中与x最匹配的子段。使用这种方法解决了波峰波谷对不齐，以致相互抵消的问题。
然后用基于线性代数方法，将公式13展开成公式15：
最终可利用瑞利商公式加以简化：
瑞利商R(M,x)的一个重要的性质是：R的最大值等于矩阵M最大的特征值，最小值等于矩阵M最小的特征值。此时，就不用太考虑R(M,x)中的x(即本问题中的uk)。公式13被简化成以下算法：
算法二：ShapeExtraction()根据簇的当前质心C和簇内的所有点X，计算更合理的质心C'。
line2: 遍历簇内所有的点X(i)
line3: 计算各点与质心的距离dist以及其中与质心最为相似的片断x'
line4: 将最为相似的片断加入X'
line5: X'转置与X相乘生成一个方阵（X的平方）
line6: 创建用于正则化的矩阵Q
line7: 正则化后生成矩阵M
line8: 取矩阵M对应最大特征值时的特征向量，以实现对X'的特征抽取
（以上说明为个人理解，不一定对，仅供参考）
基于形状的时序聚类
最终的聚类方法通过迭代实现，每次迭代分为两步：第一步重新计算质心，第二步根据每个序列与新质心的距离将它们重新分配到不同的簇中；一直循环迭代到标签不再变化为止。
算法三：聚类的完整过程由 k-Shape() 实现：
其中X是所有序列，k是簇的个数，IDX是标签。
line3: 在标签稳定前&迭代次数不超过100次的条件下，不断迭代
line4-10：根据簇中的元素重新计算每个簇的质心C
line11-line17：计算每个序列与各个质心的距离，并将它分配到新的簇中（重新打标签）。
时间复杂度
K-Shape算法每次迭代所需时间为：
O(max{n·k·m·log(m), n·m^2, k·m^3})
其中n是实例个数，k是簇个数，m是序列长度。可见，该算法大部分的计算代价依赖于时间序列的长度m。然而，这个长度通常比时间序列的数目小得多，因此，对m的依赖不是瓶颈。在m非常大的极少数情况下，可以使用分段或降维方法来有效地减小序列的长度。
模型效果
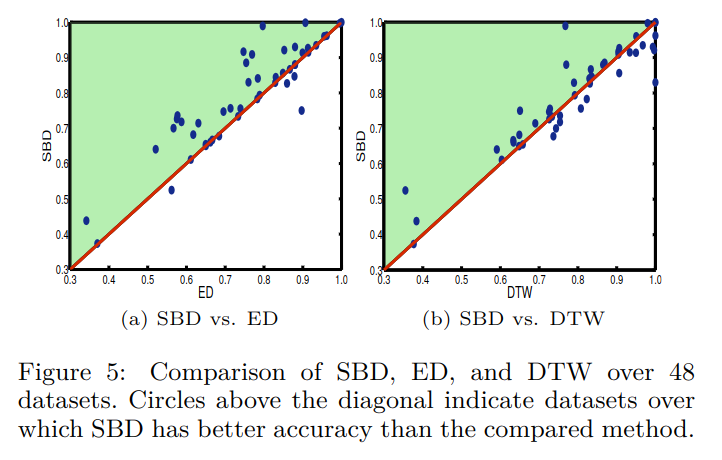
图-5对比了K-Shape、ED和DTW模型效果，可以看到绝大多数情况下，SBD好于ED，部分情况下SBD好于DTW。但SBD比DTW好在它速度更快。
