浮点型数据在内存中存储样式

double和float都属于浮点型，double是双精度浮点型，8字节，16位有效位；float是单精度浮点型，4字节，7位有效位。

 

一. 基本原则

 

1. 存储方式遵循IEEE规范（科学计数法，表示方式为1.xxx * m^n），float是IEEE R32.24（float4字节，32位，其中8位是阶码位） ,double是R64.53（double8字节，64位，其中11位是阶码位）

 

2. 阶码：用于存储科学计数法中的指数数据，并且采用移位存储

float最高位1位为符号位，接下来8位是阶码位，剩余23位为尾数位

double最高位1位为符号位，接下来11位是阶码位，剩余52位为尾数位

 

3. 尾数位：采用科学计数法表示，整数部分只能有一个1，不保存到尾数位中

 

二. 需要提前知道

 

1. 移位存储

阶码位采用移位存储，用以表示指数，将移位存储的二进制成为移码（还真是各种码：源码 反码 补码 移码）

移码是指数加上127后的值（即偏移量为127），即127相当于0，小于127为负，大于127为正，这里的127是将阶码位转为十进制之后相比较的值，比如float类型的阶码位存储了0111 1110，转为十进制为126，126 - 127 = -1，即指数为-1，2^(-1)

 

2. 十进制小数转为二进制小数

二进制和十进制一样，也有小数，与整数位以“.”隔开，以“.”为分界点，左侧的为整数部分，计算方式为2^n(n为整数)，右侧为小数部分，计算方式为2^(-n) (n为整数)，2^(-1) = 1 / 2^1 = 0.5,  2^(-2) = 1 / 2^2 = 0.25, 2^(-3) = 1 / 2^3 = 0.125

 

三. float举例说明

 

1. float tmp = 1.5; 整数部分为1，小数部分为0.5 = 2^(-1)，即十进制1.5对应二进制1.1，转换为科学计数表示方式为1.1 * 2^0，即指数为0，则阶码位为127，在内存中存储为

 

 

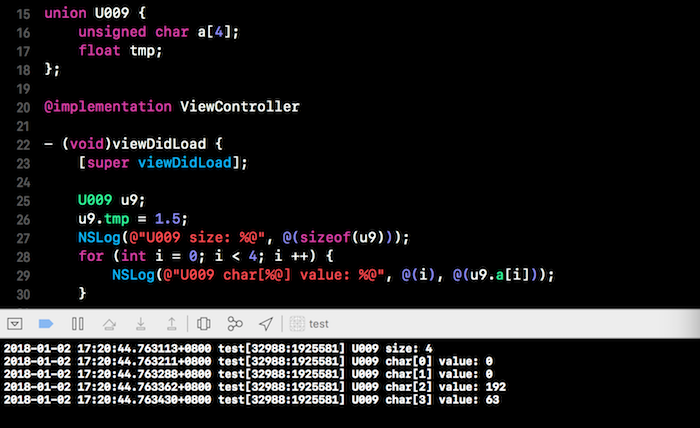
十进制1.5对应二进制1.1，因为科学计数法整数部分只有一位且为1，所以不保存整数部分的1，我觉得这也是为什么第三部分叫“尾数位”的原因

 

2. float tmp = 0.2; 按照上一步的计算会发现二进制小数部分会无限循环，因为尾数位有长度限制，就会产生精度丢失